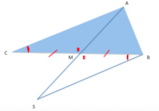
[math]\bar{AM}[/math]
di un triangolo [math]ABC[/math]
di un segmento [math]\bar{MD}[/math]
congruente a [math]\bar{AM}[/math]
, dimostra che [math]ABDC[/math]
è un parallelogramma.

Svolgimento
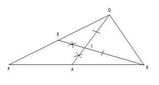
Per dimostrare che un quadrilatero è un parallelogramma, si deve dimostrare che i suoi lati opposti siano congruenti.Per farlo, prendiamo in considerazione i triangoli
[math]ACM[/math]
e [math]BMD[/math]
; essi hanno:
- AMC ≅ BMD perché angoli opposti al vertice;
- CM ≅ MB perché segmenti creati da una mediana;
- AM ≅ MD per ipotesi.
Quindi, avendo due lati e l'angolo fra essi compreso congruenti, per il primo criterio di congruenza dei triangoli,
[math]ACM[/math]
e [math]BMD[/math]
sono congruenti.Possiamo quindi affermare che AC ≅ BD, perché lati opposti ad angoli congruenti.
Con un ragionamento analogo, dimostriamo che AB ≅ CD considerando i triangoli
[math]AMB[/math]
e [math]CMD[/math]
; essi hanno:
- AMB ≅ CMD perché angoli opposti al vertice;
- CM ≅ MB perché segmenti creati da una mediana;
- AM ≅ MD per ipotesi.
Quindi, avendo due lati e l'angolo fra essi compreso congruenti, per il primo criterio di congruenza dei triangoli,
[math]AMB[/math]
e [math]CMD[/math]
sono congruenti.Possiamo quindi affermare che anche AB ≅ CD , perché lati opposti ad angoli congruenti.
Di conseguenza, il quadrilatero
[math]ABCD[/math]
, avendo i lati opposti congruenti, è un parallelogramma.