_francesca.ricci
di _francesca.ricci
(70 punti)
2' di lettura
Sia
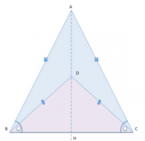
[math]ABC[/math]
un triangolo isoscele di base
[math]BC[/math]
e siano rispettivamente
[math]D[/math]
e
[math]E[/math]
due punti dei lati
[math]AB[/math]
e
[math]AC[/math]
tali che
[math]AD = AE [/math]
. Prolunga il segmento
[math]DE[/math]
di due segmenti
[math]DH[/math]
e
[math]EK[/math]
entrambi congruenti a
[math]DE[/math]
.

Dimostra che

[math]HB = KC[/math]
e che
[math]HC = KB[/math]
.

Svolgimento

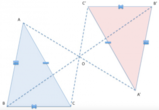
Consideriamo i triangoli
[math]BHD[/math]
e
[math]CKE[/math]
; essi hanno:
  • [math]HD = EK[/math]
    per ipotesi;
  • [math]DB = EC[/math]
    per costruzione, essendo
    [math]AD = AE [/math]
    due segmenti costruiti sui lati di un triangolo isoscele;
  • [math]\hat{HDB} = \hat{KEC}[/math]
    , poiché angoli opposti al vertice di angoli alla base di un triangolo isoscele
    [math] (ADE) [/math]
Di conseguenza, per il primo criterio di congruenza dei triangoli, avendo due lati e l’angolo fra essi compreso congruente, i triangoli
[math]BHD[/math]
e
[math]CKE[/math]
sono congruenti.
Possiamo quindi affermare che
[math]HB = KC[/math]
, poiché lati opposti ad angoli congruenti.

Consideriamo ora i triangoli

[math]BHK[/math]
e
[math]CKH[/math]
; essi hanno:
  • [math]BH = CK [/math]
    per la precedente dimostrazione;
  • [math]HK[/math]
    in comune;
  • [math]\hat{BHK} = \hat{CKH}[/math]
    , per la precedente dimostrazione.
Di conseguenza, per il per il primo criterio di congruenza dei triangoli, avendo due lati e l’angolo fra essi compreso congruente, i triangoli
[math]BHK[/math]
e
[math]CKH[/math]
sono congruenti. In particolare risulta che
[math]HC = KB[/math]
poiché lati opposti ad angoli congruenti.
Vuoi approfondire Geometria - Formule e problemi di geometria con un insegnante esperto?
Trovalo su Ripetizioni.it