Risoluzione
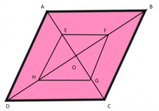
Essendo[math]M[/math]
punto medio di [math]\bar{AB}[/math]
e [math]N[/math]
punto medio di [math]\bar{DC}[/math]
sappiamo che:
[math]\bar{AM} = \bar{MB}[/math]
[math]\bar{DN} = \bar{NC}[/math]
Possiamo considerare i lati obliqui del trapezio come due trasversali che tagliano un fascio di rette parallele.
Dal teorema del fascio di parallele sappiamo che in un fascio di rette parallele tagliate da due trasversali a segmenti congruenti su una trasversale corrispondono segmenti congruenti sull’altra.
In questo caso, avendo che a due segmenti congruenti (
[math]\bar{DC} = \bar{MBb}[/math]
) corrispondono altri due segmenti congruenti ( [math]\bar{DN} = \bar{NC}[/math]
) , possiamo affermare che il segmento [math]\bar{MN}[/math]
è parallelo alle due basi del trapezio.

Prendiamo in considerazione la diagonale
[math]\bar{AC}[/math]
; dobbiamo dimostrare che [math]\bar{AO} ≅ \bar{OC}[/math]
.Consideriamo i triangoli
[math] ACD[/math]
e [math]OCN[/math]
; essi hanno:- [math]\hat{ACD}[/math]in comune;
- [math]\hat{DAC} ≅ \hat{NOC}[/math]perché angoli corrispondenti formati dalle parallele[math]\bar{AD}[/math]e[math]\bar{MN}[/math]e dalla trasversale[math]\bar{AC}[/math];
- [math]\hat{ADC} ≅ \hat{ONC}[/math]perché angoli corrispondenti formati dalle parallele[math]\bar{AD}[/math]e[math]\bar{MN}[/math]e dalla trasversale[math]\bar{DC}[/math];
[math]ACD[/math]
e [math]OCN[/math]
sono simili. Possiamo quindi dire che i loro lati sono in proporzione.Sapendo che al triangolo
[math]ACD[/math]
appartiene il lato [math]\bar{DC}[/math]
e che al triangolo [math]OCN[/math]
appartiene il lato [math]\bar{NC}[/math]
, e che [math]\bar{MN} = 2 \bar{NC} [/math]
, possiamo affermare che le misure del primo triangolo stanno alle misure del secondo come 2 sta ad 1.Di conseguenza, anche il lato
[math]\bar{AC}[/math]
sarà il doppio del lato [math]\bar{OC}[/math]
, e quindi:
[math]\bar{MN} = 2 \bar{OC}[/math]
[math]\bar{AC} = \bar{AO} + \bar{OC} \to \bar{AO} = \bar{OC}[/math]
Con un ragionamento analogo, si dimostra che anche la diagonale
[math]\bar{BD}[/math]
viene divisa in due parti uguali dal segmento [math]\bar{M}[/math]