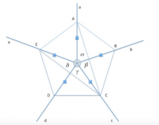
Siano l'arco
[math]AB[/math]
e l'arco [math]CD[/math]
due archi congruenti di una circonferenza (A,B,C,D nell'ordine). Dimostrare che [math]BC||AD[/math]
Osserviamo il disegno.
Ricordiamo inoltre che due angoli hanno la stessa ampiezza se insistono sul medesimo arco, o su archi congruenti.
In base a ciò, possiamo dire che gli angoli alla circonferenza
[math]hat(CAD)[/math]
e [math]hat(BCA)[/math]
sono congruenti perchè insistono su archi congruenti per ipotesi. Ora consideriamo le rette su cui giacciono i segmenti
[math]\bar{BC}[/math]
e[math]\bar{AD}[/math]
e la loro trasversale su cui giace [math]\bar{AC}[/math]
. Per i criteri di parallelismo [math]\bar{BC}[/math]
e [math]\bar{Ad}[/math]
sono paralleli in quanto hanno una coppia di angoli alterni interni congruenti. Pertanto la dimostrazione è completa.
FINE