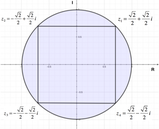
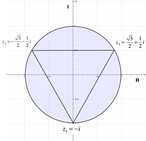
Per risolvere un’equazione di questo tipo dobbiamo procedere considerando la rappresentazione esponenziale dei numeri complessi.
Un numero complesso
[math]z[/math]
può essere scritto in questo modo:
[math] z = \rho e^{i \theta}[/math]
dove
[math]\rho[/math]
rappresenta il modulo di
[math]z[/math]
, mentre
[math]\theta[/math]
è un angolo che rappresenta l’argomento del numero complesso.
L’angolo
[math]\theta[/math]
servirà per determinare la posizione delle soluzioni sulla circonferenza goniometrica; ricordiamo, infatti, che vale la seguente uguaglianza:
[math] e^{i \theta} = \cos(\theta) + i \sin (\theta) [/math]
La nostra equazione, quindi, può essere espressa in una nuova forma, più facilmente risolvibile:
[math] (\rho e^{i \theta})^4 = 1 \to \rho^4 e^{ 4i \theta} = 1 [/math]
Notiamo che, affinché l’uguaglianza sia verificata, è necessario che
[math] \rho = 1[/math]
e che
[math] e^{i \theta} = e^0 = 1[/math]
.
[math] e^{ 4i \theta} = e^{0} = 1[/math]
Possiamo quindi impostare il seguente sistema:
[math] \begin{cases} \rho^4= 1 \\4 \theta = 0 + 2k \pi \end{cases} [/math]
Nella risoluzione dell’equazione dobbiamo tener conto del fatto che, poiché l’esponente di
[math]z[/math]
è 4, avremo esattamente quattro soluzioni; ciò significa che i valori che può assumere il coefficiente
[math]k[/math]
sono
[math] 0, 1, 2, 3[/math]
.
Dalla prima equazione risulta evidente che deve essere
[math] \rho = 1[/math]
.
Risolviamo ora la seconda equazione; ricordiamo che sono validi tutti gli angoli
[math]\theta[/math]
multipli di
[math]360°[/math]
:
[math] e^{ 4i \theta} = e^{0} \to 4\theta = 2k\pi [/math]
Quindi:
[math] \theta = \frac{2k\pi}{4} = \frac{k\pi}{2} [/math]
Determiniamo i tre angoli che individuano le tre soluzioni dell’equazione:
[math] k = 0 \to \theta = 0 [/math]
[math] k = 1 \to \theta = \frac{\pi}{2} [/math]
[math] k = 2 \to \theta = \pi [/math]
[math] k = 3 \to \theta = \frac{3\pi}{2} [/math]
Ora dobbiamo scrivere i numeri complessi
[math] z_1[/math]
,
[math] z_2[/math]
,
[math] z_3[/math]
e
[math] z_4[/math]
nella forma
[math] a + ib[/math]
.
Per farlo, ricorriamo alla rappresentazione trigonometrica dei numeri complessi, ovvero sfruttiamo l’uguaglianza:
[math] z = e^{i \theta} = \cos(\theta) + i \sin (\theta) [/math]
Nel primo caso abbiamo:
[math] z_1 = \cos(0) + i \sin (0) = 1 [/math]
Nel secondo caso:
[math] z_2 = \cos(\frac{\pi}{2}) + i \sin (\frac{\pi}{2}) = i [/math]
Nel terzo caso:
[math] z_3 = \cos(\pi) + i \sin (\pi) = -1 [/math]
Infine, la quarta soluzione è:
[math] z_3 = \cos(\frac{3\pi}{2}) + i \sin (\frac{3\pi}{2}) = -i [/math]
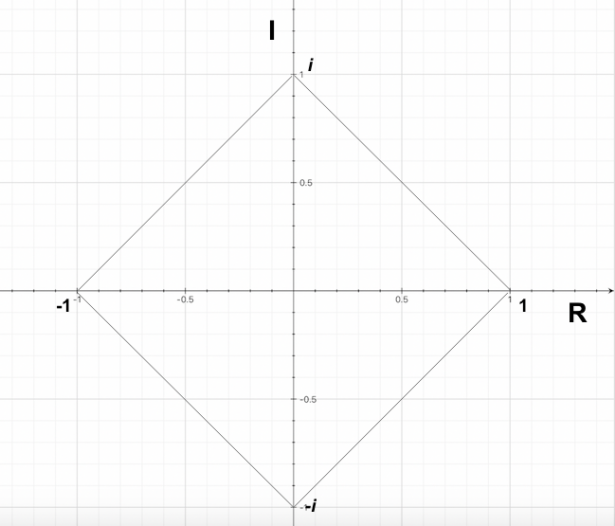
Come possiamo notare, le soluzioni sono due reali e due complesse coniugate; rappresentando le soluzioni ottenute su una circonferenza goniometrica possiamo notare che esse individuano i vertici di un quadrato.
Potrebbe interessarti anche