Farmaco

Il recente numero di Almanacco della scienza di Micromega - come si intuisce dal titolo - è interamente dedicato alla scienza, settore culturale piuttosto maldigerito dal mondo intellettuale italiano e di conseguenza largamente ignorato da gran parte delle persone.
L'autore consiglia caldamente di leggere questo numero, che ospita una decina di brevi saggi e interviste di personaggi famosi che danno un contributo sostanziale all'avanzamento della scienza; ad esempio Carlo Rovelli personaggio di punta per la Teoria della gravità quantistica a loop.

Desideriamo soffermarci sul saggio di Silvio Garattini, direttore di un importante istituto di ricerca farmacologica.

Che tratta di omeopatia (intesa in senso lato), diete, vaccini. E lamenta l'ignoranza di molti che si affidano a terapie prive di basi scientifiche. Tale testo - dieci pagine - si legge con grande facilità ed è molto chiaro ed efficace.

Da esso vogliamo prendere pretesto per proporre un esempio, molto semplificato, di come si potrebbe immaginare di verificare l'efficacia di un farmaco. E dimostrare in tal modo che ricerca farmacologica è un'attività ancorata a solidi criteri scientifici.

Immaginiamo una determinata malattia, abbastanza diffusa tra la popolazione e ben studiata dalla medicina. Per questa malattia esiste un farmaco abbastanza efficace in diversi pazienti, ma poco attivo in altri. Una casa farmaceutica concorrente, dopo lunghe ricerche, ha sviluppato una molecola alternativa (in farmacologia si chiama principio attivo). Tutti gli studi preparatori e la sperimentazione pre-clinica (animale) hanno dato esito positivo e si inizia la sperimentazione clinica (su persone). Come è noto tale sperimentazione è la fase più complessa e costosa dello sviluppo prodotto. Consta di diverse fasi e sotto fasi, ciascuna delle quali dura qualche anno. Si realizza secondo la normativa di legge e sotto il controllo del Comitato Etico.

Immaginiamo sia stato ormai accertato che il farmaco ha una certa efficacia. Si pianifica allora uno step di indagine allo scopo di verificare il dosaggio opportuno. Si identificano due livelli di dosaggio: basso e medio. Si decide che il campione di persone (malati) da sottoporre a sperimentazione sia di 30 persone. Come si procede?

Si scelgono a caso (random) le 30 persone, affette da tale malattia, da sottoporre, con il loro consenso, a sperimentazione. Il campione viene suddiviso in tre gruppi di 10 persone, e la distribuzione delle persone per gruppo viene fatta a caso. Il primo gruppo, detto gruppo di controllo, riceve il farmaco preesistente, il secondo gruppo riceve il farmaco nuovo a bassa dose, il terzo il farmaco nuovo a media dose. L'esperimento è condotto in doppio cieco, vale a dire che i pazienti (primo cieco) ed i medici (secondo cieco) ignorano quale paziente abbia ricevuto quale farmaco. In tal modo si evitano pregiudizi (bias) che potrebbero compromettere la validità della sperimentazione.

Supponiamo che lo stato clinico del paziente nei riguardi della malattia sia evidenziato da un'analisi del sangue che chiameremo XV. Al disotto di XV=40 il paziente è malato. Si somministrano i farmaci per un certo periodo alla dose prescelta per ogni gruppo. E si misura nuovamente il valore XV nei pazienti. Si ritiene che la variazione di XV tra inizio e fine terapia rappresenti l'efficacia del farmaco somministrato.

I dati e risultati della sperimentazione sono passati allo statistico che li dovrà elaborare. Egli sa come sono costituiti i gruppi e dunque elabora i dati sperimentali suddividendoli per i tre gruppi sulla base della seguente tabella.

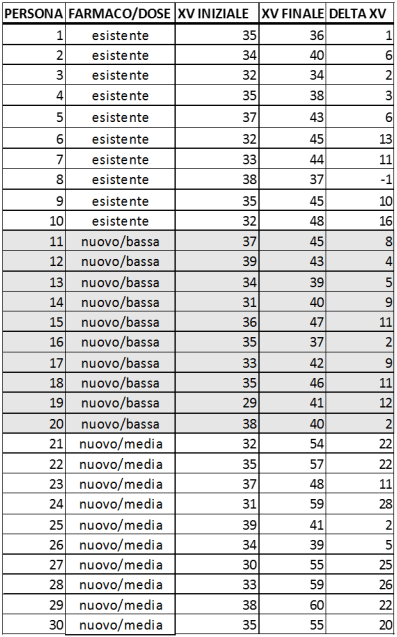
E' evidente che i valori iniziali e le variazioni di XV sono diversi per i pazienti anche all'interno di ogni gruppo, perché il grado di malattia iniziale è diverso da individuo a individuo ed inoltre l'effetto del farmaco è diverso perché la reazione biologica dell'organismo è variabile. Per eliminare queste variabilità la cosa naturale è prendere la media della variazione di XV all'interno di ogni gruppo. Ossia fare le medie per gruppo.

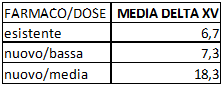
Calcolate queste medie sembra che passando dal primo al secondo al terzo gruppo si manifesti un'efficacia crescente. Possiamo dunque concludere che sicuramente il nuovo farmaco a dose bassa è più attivo di quello esistente e che a dose media lo è ancora di più? Potremmo farlo solo se avessimo scelto, per ogni gruppo, un insieme vastissimo, in teoria infinito (la popolazione). Purtroppo abbiamo scelto solo 10 persone (campione), per evidenti e validi motivi, pratici ed economici. I nostri tre gruppi sono costituiti da piccoli campioni casuali ed è ben possibile che la media di un piccolo campione sia migliore o peggiore di quello della popolazione. Quello che ci interessa è, per quanto possibile, usare questi piccoli campioni per dedurre il comportamento dei farmaci/dosi sulle relative popolazioni. Ci serve dunque un criterio per passare dal piccolo al grande. Evitando di prendere degli abbagli. Qui ci possono aiutare la matematica e la statistica. La tecnica che useremo si definisce Analisi di Varianza ed è brevemente riportata in APPENDICE.

Si tratta di una metodologia piuttosto semplice e rapida. Tuttavia è possibile evitare di fare i calcoli, basta applicare la Analisi Dati di EXCEL usando Analisi di Varianza ad un Fattore.

Per farlo si comincia a riscrivere la tabella dei valori DELTA XV per righe e colonne. Ogni riga rappresenta un diverso trattamento (i.e. farmaco), ogni colonna il risultato del trattamento (effetto) su un diverso paziente:

Si assegna come input alla routine EXCEL la matrice (qui sopra scritta) dei trattamenti e il livello di significatività

, come riportato nell'immagine sotto:

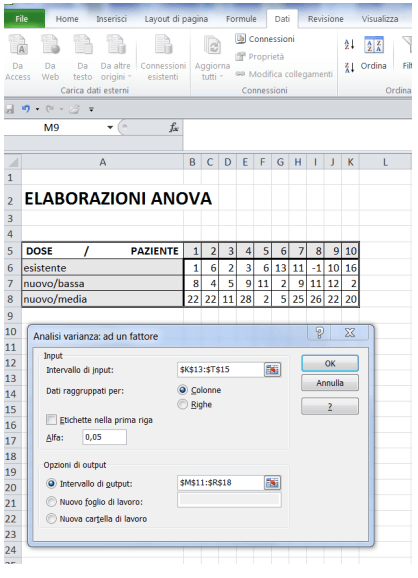
E si ottiene, nell'intervallo di OUPUT, la tabella che contiene le variabili statistiche desiderate: Somme Quadratiche (SQ), Gradi di Libertà (gdl), Medie Quadratiche (MQ, vale a dire varianze), F (osservato), F(crit, vale a dire teorico), come riportato sotto.

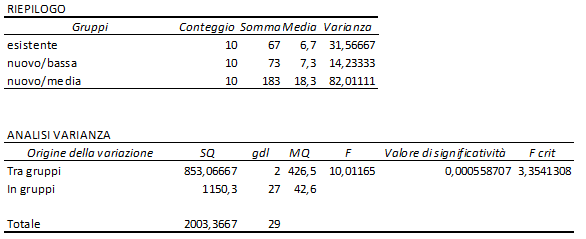
Si vede quindi che F osservato (10,01) è molto maggiore di F crit (3,35). Pertanto si conclude respingendo l'ipotesi H0. Non è quindi vero che le popolazioni dei tre trattamenti hanno la stessa media. Il che vuol dire che gli effetti dei tre trattamenti sono diversi.

Non abbiamo dubbi che il trattamento nuovo/media è quello più efficace.

Possiamo anche fare dei confronti a due a due fra i trattamenti.

Se ripetiamo l'analisi di varianza fra esistente e nuovo/bassa otteniamo:

Qui risulta F osservato

La tabella sopra riporta anche il Valore di significatività (0,782, vale a dire 78,2%). Di cosa si tratta? E' il valore si significatività (α) corrispondente a F osservato. Essendo un valore molto grande (molto più grande del valore richiesto 5%), ci conferma che non possiamo respingere l'ipotesi H0.

Questo risultato non era così facilmente prevedibile. Infatti la media campionaria del nuovo/bassa è quasi del 10% superiore a quella dell'esistente. A spanne si pensava che fosse più efficace. Ma l'analisi di varianza ha smentito questa idea. Statisticamente non c'è alcuna differenza.

Il confronto fra esistente e nuovo/media è qui sotto riportato:

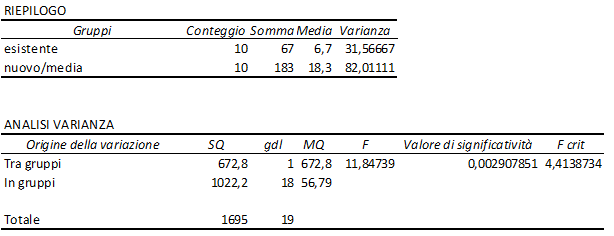
E vediamo che F osservato (11,84) è molto superiore a F crisi (4,41). Se ne conclude che il nuovo/media è molto più efficace dell'esistente. Con un rischio di sbagliare pari allo 0,29% che è estremamente basso.

APPENDICE: ANALISI DI VARIANZA

Immaginiamo di fare delle prove sperimentali applicando ad un sistema definito diversi trattamenti. Per trattamenti intendiamo dei fattori sperimentali. Ad esempio farmaci diversi applicati a diversi individui, oppure fertilizzanti diversi applicati a diversi campi. Per ogni trattamento replichiamo le prove volte. Per ogni trattamento/replica otterremo un risultato Yij. Scriviamo ora trattamenti (T1, T2,..Tm) per identificare le righe, le repliche (R1, R2,…Rn) per identificare le colonne e scriviamo i rispettivi risultati ( Yij) in una matrice m*n, sotto riportata:

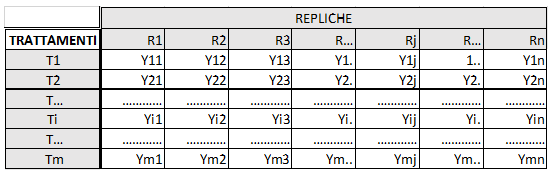
Scopo dell'Analisi di Varianza è determinare se applicando i diversi trattamenti si sono ottenuti effetti diversi. Come detto prima vogliamo confrontare le medie per riga tra di loro, ma la statistica richiede anche di costruire delle varianze.

La generica media per riga è data da:

[ \begin{equation} Y_{med_i} = frac{\sum_j^{1,n} Y_{ij}}{n} label{eq1} end{equation} ]

Le medie campionarie

così calcolate sono delle stime campionarie delle medie delle popolazioni ( ). Evidenziamole in questa tabella:

La media generale, vale a dire la media delle medie campionarie è: [ Y_{med} = frac{\sum_i \sum_j Y_{ij}}{nm} ]

Ora si costruiscono le Somme Quadratiche:

( SQSP = n \sum_i (Ymed_i - Ymed)^2 ) somma quadratica spiegata

( SQRES = \sum_i \sum_j (Y_{ij} - Ymed_i)^2 ) somma quadratica residua, vale a dire non spiegata

( SQTOT = \sum_i \sum_j (Y_{ij} - Ymed)^2 ) somma quadratica totale

E vale la seguente correlazione: ( SQTOT = SQSP + SQRES )

SQSP si chiama somma quadratica spiegata, in quanto è dovuta al (presunto) effetto dei trattamenti rispetto alla media Ymed. Mentre SQRES è definita somma quadratica residua perché non è spiegata dai trattamenti, ed è quindi riconducibile alla variabilità naturale dei dati oppure all'errore sperimentale.

Ciascuna delle somme quadratiche possiede un determinato numero di gradi di libertà (gdl). In generale il numero di gradi di libertà è dato dal numero dei dati in oggetto diminuito del numero di parametri calcolati con tali dati. Dividendo le somme quadratiche per il rispettivo gdl si ottengono, infine le media quadratiche. Come da tabella seguente

Le medie quadratiche sono varianze.

Il rapporto tra la media quadratica spiegata e quella residua genera un variabile statistica denominata F di Fisher.

[ \begin{equation} F = frac{MQSP}{MQRES} label{eq2} end{equation} ]

Il valore di F fornito dalla ( \ref{eq2} ) si definisce F osservato, perché è riconducibile ai dati sperimentali (osservati), elaborati come sopra riportato.

Che uso facciamo dell'F osservato? Lo confrontiamo con la variabile statistica F (teorica). La sua distribuzione, che definiamo

è riportata nella figura sotto. Essa è stata inventata da Fisher e Snedecor ed è una funzione nota - piuttosto complessa - che dipende da due parametri, che sono esattamente i gradi di libertà delle medie quadratiche a numeratore e denominatore della ( \ref{eq2} ).

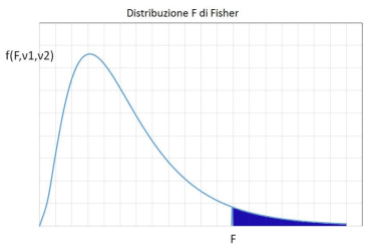
In ascisse si riportano i valori di F, in ordinate la sua funzione di distribuzione f(F). L'area sotto la curva, tra due punti qualsiasi F1 ed F2 rappresenta la probabilità che F cada tra questi due punti. L'area sotto la curva (da zero a infinito) è unitaria.

L'area blu evidenziata a destra del valore F (detta zona critica) rappresenta la significatività

. Dunque è la probabilità che F cada nell'intervallo ( [F +infty] ).

Esiste, ovviamente, una corrispondenza biunivoca tra ( alpha ) ed F, nel senso che ad ogni valore di

assegnato corrisponde un determinato valore di F.

Si assegna ora il valore di

, di solito . Il test di ipotesi per questa situazione si formula in questo modo:

• Ipotesi
  [math] Ho: \mu_1= \mu_2 = \ldots = \mu_m [/math]
  vale a dire le medie delle popolazioni sono eguali. In altre parole, gli effetti dei diversi trattamenti sono identici
• Ipotesi
  [math] H1 [/math]
  : almeno due medie delle
  [math] m [/math]
  popolazioni sono diverse (vale a dire almeno due trattamenti danno effetti diversi)

si definisce Ipotesi Nulla (nessuna differenza), mentre si chiama Ipotesi Alternativa.

Il test F-di Fisher, che abbiamo ora definito, consiste nel confrontare il valore di F osservato con F della curva teorica sopra riportata.

Se risulta:

F osservato , vale a dire se F osservato cade (sull'asse delle ascisse) a sinistra dell'area blu, si accetta l'ipotesi

.

Se invece F osservato> F, vale a dire se F osservato cade nella zona critica, si respinge l'ipotesi

e si accetta l'ipotesi .

BIBLIOGRAFIA

Silvio Garattini-Curarsi con l'acqua fresca- Almanacco della Scienza-MICROMEGA-5/2015

Murray R. Spiegel - Statistica - McGraw Hill

http://mathworld.wolfram.com/F-Distribution.html