Fionda

In un precedente articolo, dedicato al libro/film Il sopravvissuto-The Martian, ho citato brevemente l'Effetto Fionda. Ritorno sull'argomento per descrivere l'effetto e mostrare con un esempio pratico come si manifesta questo fenomeno. Prima di far questo, tuttavia, è necessario inquadrare il fenomeno nell'ambito delle manovre spaziali e spiegare perché l'Effetto Fionda è importante dal punto di vista pratico.

ASTRONAUTICA

Da diversi decenni vengono lanciate sonde spaziali (probes) per varie attività di interesse, quali ad esempio il posizionamento dei satelliti, il sorvolo di pianeti per misurazioni a distanza. Una caratteristica saliente di tutte queste attività è il raggiungimento di orbite stazionarie o il passaggio da un'orbita all'altra del medesimo pianeta/satellite oppure tra diversi pianeti/satelliti.

Queste manovre spaziali richiedono un'azione meccanica di tipo impulsivo, che possono essere realizzate in diversi modi. In ogni caso la grandezza che individua l'azione impulsiva è denominata (Delta v) Come si può intuire (Delta v) significa variazione di velocità.

Ci potremmo domandare per quale ragione occorre realizzare un (Delta v). Ecco un esempio per spiegarlo. Supponiamo di voler mettere in orbita un satellite attorno alla Terra, su di un'orbita circolare a 50 km di quota. Lanciamo allora un razzo pluristadio che parte dalla Terra a

e, dopo la separazione dei diversi stadi, mette in orbita il satellite. Perché quest'ultimo resti stabilmente in orbita occorre che la sua accelerazione centripeta eguagli l'attrazione gravitazionale. Quindi deve essere: [ m frac{v^2}{d} = frac{kmM}{d^2} ]
che risolta fornisce: [ v = \sqrt{frac{kM}{d}} ]

Introducendo i valori numerici si ottiene (v = 7900, m/s = 7,9, km/s) . Di conseguenza (Delta v = 7,9, km/s )

Il diagramma sotto riportato (rif. 2) mostra i (Delta v) effettivi, per diverse manovre che riguardano la Terra ed i pianeti/satelliti vicini.

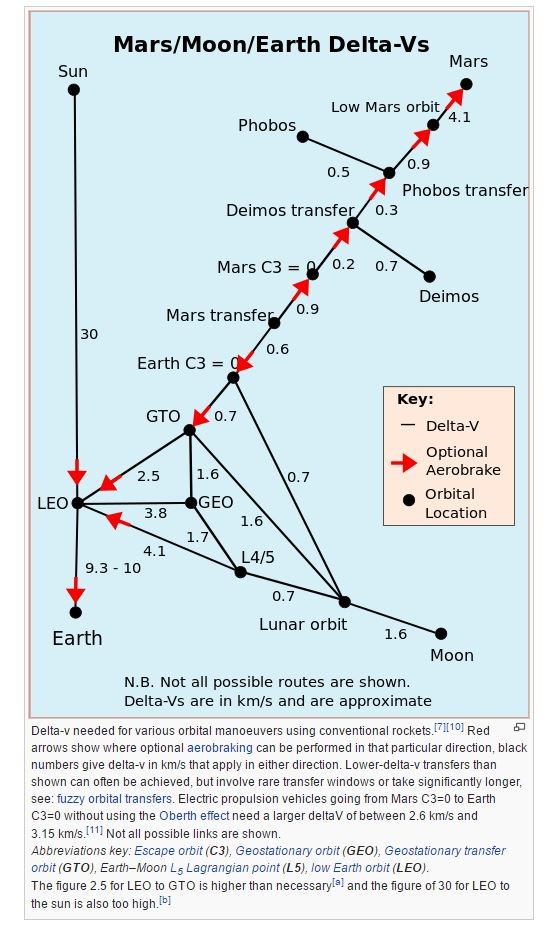
Da notare il grande (Delta v) richiesto per passare dalla superficie terrestre (Earth) a un'orbita terrestre bassa (LEO). I valori del diagramma sono in km/s.
Esistono diversi sistemi per realizzare un (Delta v). I più usati sono la propulsione e l'effetto fionda.

PROPULSIONE

La propulsione consiste nell'espulsione di gas ad alta velocità. E' questo il mezzo usato per far muovere i razzi vettori nello spazio. Per il terzo principio della dinamica alla spinta esercitata dal razzo sui gas corrisponde una spinta uguale e contraria, che permette al razzo di acquistare accelerazione. Questo fenomeno può essere approssimato dall'equazione di Tsiolkovsky (rif.3): [ Delta v = v_e ln frac{m_0}{m_f} ]

Essa afferma che il (Delta v) è dato dal prodotto della velocità dei gas espulsi (

) (rif.4) per il logaritmo del rapporto tra la massa iniziale del mezzo () e la sua massa finale (). Notiamo che la differenza ( ) rappresenta la quantità totale di combustibile espulso come gas di scarico. In altri termini quanto maggiore è la frazione di massa espulsa, tanto maggiore è la variazioni di velocità ottenibile. Il diagramma sotto riporta l'equazione in termini adimensionali.

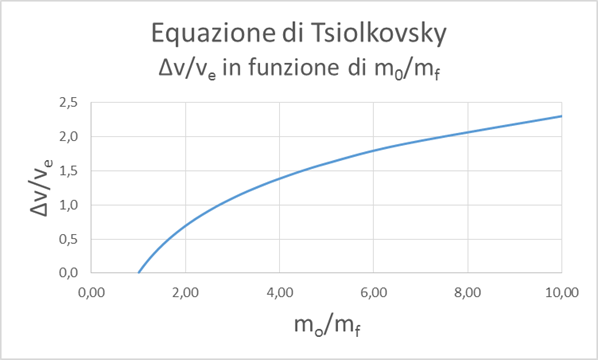
E' abbastanza evidente che il rapporto

incontra un limite naturale. Per quanto nella progettazione spaziale si faccia uso di materiali leggeri, la massa totale non può certo essere costituita solo da propellente. Pur ricorrendo all'intelligente sistema dei razzi pluristadio, di fatto non può essere inferiore al 10% di . La velocità dei gas espulsi ()) dipende dalla scelta del mezzo di propulsione (combustibile + comburente), comunque con l'attuale tecnologia non può superare determinati valori (circa 5 km/s); questo vuol dire che, sulla base dell'equazione di Tsiolkovsky, il (Delta v) non può superare circa 11,5 km/s. In altri termini le manovre orbitali di tipo propulsivo incontrano dei limiti tecnologici.

L'equazione di Tsiolkovsky a rigore è valida nello spazio vuoto, lontano da corpi celesti - vale a dire trascurando le forze gravitazionali - e in assenza di resistenze aerodinamiche. Nella realtà il (Delta v) effettivo è un po' superiore. Sappiamo che durante il lancio di un razzo dalla Terra il primo stadio incontra una grande resistenza da parte dell'atmosfera e inoltre occorre vincere la forza gravitazionale del pianeta: questo richiede notevole consumo di propulsione.

Il lettore che desidera capire bene l'equazione di Tsiolkovsky può leggere l'interessante articolo con la dimostrazione (rif. 5). Al proposito ricordiamo che il fisico Richard Feynman - premio Nobel per l'Elettrodinamica Quantistica - sosteneva che si può dire di aver compreso a fondo un fenomeno fisico solo quando si riesce a ricavare le equazioni che lo descrivono.

Risulta chiaro da quanto detto che numerose manovre orbitali risultano particolarmente dispendiose in termini di propulsione necessaria, talune sono impossibili.

EFFETTO FIONDA

Ecco allora che la tecnica spaziale ricorre ad una manovra ingegnosa definita Effetto Fionda (gravity assist). In modo semplificato possiamo dire che quando una sonda spaziale si avvicina a un corpo celeste in movimento, ad es. un pianeta, per effetto dell'attrazione gravitazionale la sonda scambia energia con tale corpo. Il risultato consiste in un cambiamento di traiettoria della sonda e in una variazione della sua velocità. In funzione di posizione e velocità iniziali di sonda e pianeta si realizza un effetto frenante oppure accelerante sulla sonda. Limitandoci al caso dell'effetto accelerante, è possibile imprimere alla sonda un notevole Δv , risparmiando in tal modo la propulsione. A prima vista questo effetto potrebbe apparire miracoloso. Così non è. Cominciamo a notare che il sistema pianeta-sonda, considerato isolato dal resto dell'universo conserva la quantità di moto totale ed anche l'energia totale (totale vuol dire pianeta + sonda). Questo deriva dal fatto che la forza gravitazionale è di tipo conservativo, vale a dire che il lavoro esercitato dalla forza gravitazionale si trasforma in energia cinetica e viceversa, senza fenomeni dissipativi. L'energia totale è data dalla somma di due tipi di energia: cinetica e potenziale (gravitazionale.)

[\begin{equation} E = E_c + E_g = frac{1}{2} (mv^2+MV^2) - frac{kmM}{d} = mbox{costante} label{eq1} end{equation} ]

dove

ed sono le masse mentre e sono i moduli delle rispettive velocità, è la distanza tra i baricentri delle due masse.

Ora avviene che, in pratica, nella manovra dell'effetto fionda la variazione di energia potenziale è trascurabile rispetto alla variazione di energia cinetica. Si ha dunque, di fatto, la conservazione dell'energia cinetica. In conclusione la sonda aumenta notevolmente la sua energia cinetica a spese di un'uguale diminuzione di energia cinetica del pianeta. Il quale, avendo una massa enorme rispetto alla sonda, neppure si accorge di ciò:

[ mv^2 + MV^2 = mbox{costante} ]

Notiamo un fatto essenziale: l'effetto avviene perché il pianeta è in movimento. Se fosse fermo non avverrebbe. Osserviamo che nell'equazione di conservazione dell'energia (sopra riportata) le velocità fanno riferimento a un sistema inerziale, ad esempio al Sole. Quindi

è la velocità istantanea del pianeta lungo la sua orbita, che per il breve intervallo di tempo in cui consideriamo l'effetto fionda, può essere approssimato con un moto rettilineo a velocità costante. Mentre è la velocità della sonda in avvicinamento al pianeta in modalità fly-by (sorvolo), vale a dire senza entrare nell'orbita (circolare o ellittica) planetaria.

Di fatto l'effetto fionda è usatissimo nelle missioni spaziali, anzi è considerato una tecnica indispensabile. Esso si presta a essere sommato sorvolando in successione diversi pianeti, come mostrato nel disegno sotto che riporta il lungo viaggio extra-sistema-solare della sonda Voyager 2 (rif.6).

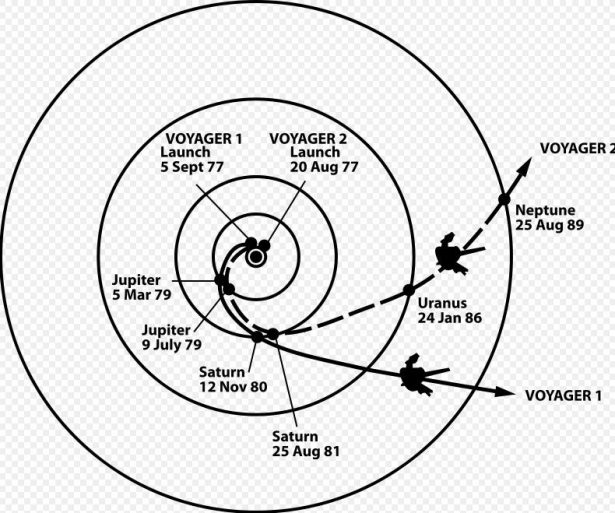
In teoria l'effetto fionda potrebbe consentire una variazione di velocità della sonda fino al doppio della velocità del pianeta. Quanto più vicino è il sorvolo, tanto maggiore è la fionda. Tuttavia esistono dei limiti pratici dovuti alla presenza dell'atmosfera planetaria che frenerebbe la sonda. Senza esagerare possiamo dire che il gravity assist (rif.7) è servito a dare una marcia in più all'esplorazione spaziale.

STORIA DELL'EFFETTO

Chi ha scoperto l'effetto fionda? Diciamo che il russo Kondratjuk ebbe delle intuizioni durante la prima guerra mondiale, poi il russo Zander (1925) fece degli studi. In seguito (1956) l'italiano Crocco propose un tour planetario che faceva ricorso alla fionda. Chi davvero comprese a fondo significato e uso e descrisse il fenomeno, fu il matematico americano Michael Minovitch, che sviluppò la teoria durante uno stage post-laurea presso la NASA nel 1961. Il rapporto NASA originale (rif.8), dimostra la potenza della fisica-matematica applicata alla simulazione del fenomeno. Purtroppo il rapporto è molto lungo (49 pagine di formule matematiche) e alquanto complesso (l'autore di quest'articolo ha desistito dalla lettura).
Dopo la scoperta di Minovich la NASA ha cominciato ad applicare il gravity assist in modo continuo ed efficace alle sue numerose missioni spaziali.
I russi già tre anni prima avevano sfruttato l'effetto nel corso di una missione con la sonda Luna3: dietro suggerimento dei loro abili matematici.

APPLICAZIONE: EFFETTO FIONDA DI GIOVE

Vogliamo ora provare a sviluppare un piccolo problema che faccia ricorso all'effetto fionda.
Supponiamo di aver inviato dalla Terra una sonda per l'esplorazione extra-sistema-solare. La sonda è ormai giunta in prossimità di Giove e vogliamo sfruttare la fionda del pianeta per un balzo extra solare. Quanto alle forze gravitazionali agenti sulla sonda assumiamo che prevalga quella di Giove (che è molto vicino) mentre quella del Sole (che è lontano) sia piccola e, in prima approssimazione, trascurabile.
Ai fini di facilitare la rappresentazione grafica formuliamo l'ipotesi semplificativa che i vettori delle velocità iniziali del pianeta e della sonda siano complanari. In tal modo il moto dei due corpi avverrà su di un piano. Assumiamo, come riferimento per lo studio del moto, un piano di assi coordinati x, y solidale con il sole. Il riferimento prescelto è di tipo inerziale, cosa che semplifica la scrittura delle equazioni. Il moto del pianeta avviene lungo la sua orbita solare. Dal momento che studio del moto dei due corpi è limitato ad un breve periodo di tempo (qualche giorno) è lecito assumere che il pianeta si muova lungo un segmento tangente alla sua orbita.

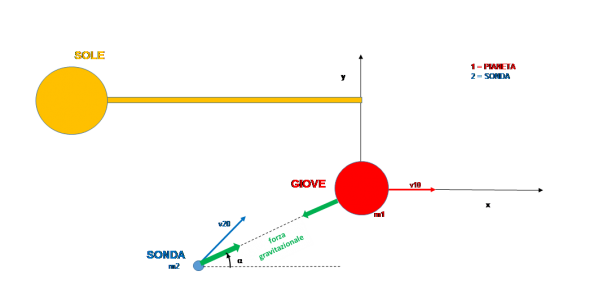
Assumiamo che all'istante iniziale (t=0) il pianeta sia nell'origine degli assi e la sua velocità sia diretta lungo l'asse x.
Il moto di entrambi i due corpi è descritto dal secondo principio della dinamica (forza = massa*accelerazione). La forza che condiziona il movimento è la reciproca attrazione gravitazionale, identificata dalla Legge di Gravitazione Universale di Newton (a 2° membro delle successive quattro equazioni).
Il secondo principio della dinamica è rappresentato da un'equazione vettoriale, che nel nostro caso piano può essere decomposta nelle sue componenti lungo i due assi coordinati:

[ m_1 frac{dv_{x_1}}{dt} = k frac{m_1 m_2}{d^2} cos (alpha) ]

[ m_1 frac{dv_{y_1}}{dt} = k frac{m_1 m_2}{d^2} \sin (alpha) ]

[ m_1 frac{dv_{x_2}}{dt} = -k frac{m_1 m_2}{d^2} cos (alpha) ]

[ m_1 frac{dv_{y_2}}{dt} = -k frac{m_1 m_2}{d^2} \sin (alpha) ]

Il sistema è completato dalle equazioni che definiscono le componenti della velocità come derivate delle spazio rispetto al tempo:

( frac{dx_1}{dt} = v_{x_1} )

( frac{dy_1}{dt} = v_{y_1} )

( frac{dx_2}{dt} = v_{x_2} )

( frac{dy_2}{dt} = v_{y_2} )

Dove (alpha) è l'angolo antiorario formato con l'asse

dal segmento che congiunge il centro del pianeta con la sonda, mentre è la distanza istantanea tra i due corpi, vale a dire la lunghezza del segmento, mentre è la costante di gravitazione universale.

Risulta dalla trigonometria:

[ cos(alpha) = frac{x_2-x_1}{d} ]

[ \sin(alpha) = frac{y_2-y_1}{d} ]

Sostituendo e semplificando si ottiene:

( frac{dv_{x_1}}{dt} = k frac{m_2}{d^3} (x_2-x_1) )

( frac{dv_{y_1}}{dt} = k frac{m_2}{d^3} (y_2-y_1 ))

( frac{dv_{x_2}}{dt} = -k frac{m_1}{d^3} (x_2-x_1) )

( frac{dv_{y_2}}{dt} = -k frac{m_2}{d^3} (y_2-y_1) )

( frac{dx_1}{dt} = v_{x_1} )

( frac{dy_1}{dt} = v_{y_1} )

( frac{dx_2}{dt} = v_{x_2} )

( frac{dy_2}{dt} = v_{y_2} )

Il Sistema di otto equazioni differenziali del 1° ordine in forma normale si risolve con la condizione iniziale:

(t=0)
(x_1= 0)
(y_1=0)
(x_2= x_{20})
(y_2= y_{20})
(v_{x_1}=v_{x10})
(v_{y2}=0)
(v_{x2}=v_{x20})
(v_{y2}=v_{y20})

Che si risolve con metodi numerici, ad es. con la routine di Runge-Kutta del 4° ordine.

Notiamo tuttavia che l'azione gravitazionale esercitata dalla sonda non ha alcun effetto sul pianeta, data la sua enorme massa, e quindi il sistema si può semplificare:

(v_{x1}= v_{x10} )

(v_{y1}= 0 )

(y_1=0 )

(x_1=v_{x10} t )

(frac{dv_{x2}}{dt} = - k frac{m_1}{d^3} (x_2-v_{x10} t))

(frac{dv_{y2}}{dt} = - k frac{m_2}{d^3}y_2)

(frac{dx_2}{dt}= v_{x2})

(frac{dy_2}{dt}= v_{y2})

In definitiva abbiamo un sistema di quattro equazioni differenziali in forma normale, che descrivono il moto della sonda, con la condizione iniziale:

(t=0 )
(x_2= x_{20} )
(y_2= y_{20} )
(v_{x2}=v_{x20} )
(v_{y2}=v_{y20} )

Il file EXCEL associato all'articolo si avvale di un semplice codice VBA di EXCEL (file allegato all'articolo) per determinare l'effetto fionda di Giove sulla sonda spaziale.

Il diagramma sotto evidenzia l'aumento di velocità della sonda provocato dalla forza gravitazionale di Giove.

Mentre il pianeta correva lungo la sua orbita alla velocità costante di circa 13000 m/s, la sonda si muoveva alla velocità di 14000 m/s lungo la sua traiettoria nel sistema solare. Per l'effetto fionda la sonda accelera fino a raggiungere la velocità massima di 26700 m/s, per poi decrescere lentamente fino a 21000 m/s. In definitiva si realizza un (Delta v) notevole, pari a 21-14 = 7 km/s. Il diagramma riporta in ascisse il tempo, misurato in secondi. L'intero fenomeno avviene nell'arco di un centinaio di ore.

Di seguito sono riportate le traiettorie dei due corpi nel loro moto rispetto al Sole.

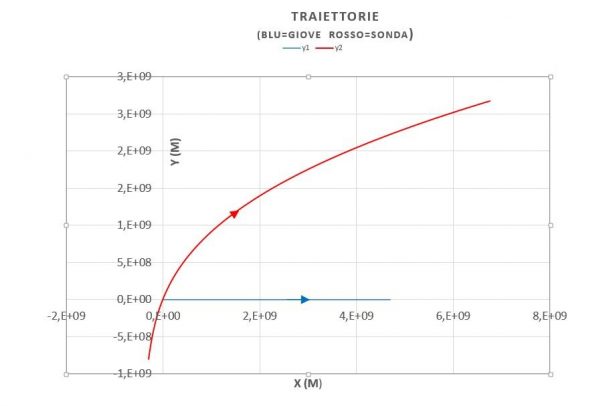
Mentre nel diagramma seguente si evidenzia la traiettoria della sonda nel suo moto relativo a Giove

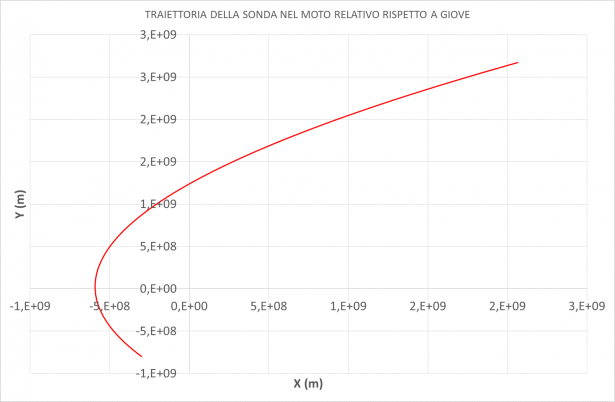
Di quale tipo di curva si tratta? Per rispondere alla domanda riprendiamo l'Equazione ((\ref{eq1})) che definisce la conservazione dell'energia totale. Questa volta, però la riscriviamo con riferimento al moto relativo della sonda (pedice r) rispetto a Giove nelle condizioni iniziali (quando t=0):

[ E = E_C + E_g = frac{1}{2} mv^2_{02r} - frac{km_1 m_2}{d_0} = 1,03993mbox{E+12} - 1,03348mbox{E+12} = 6,44917mbox{E+09}, J ]

Ora noi sappiamo che quando (E lt 0) la curva è un'ellisse, mentre quando ( E gt 0) è un'iperbole.

Dunque nel nostro caso abbiamo un'iperbole, il che vuol dire che la sonda sorvola Giove senza restare imprigionata nella sua orbita.

RIFERIMENTI

1. https://www.skuola.net/esercizi-svolti/problem-solving-avanzato/scienza-vs-fantascienza/
2. https://en.wikipedia.org/wiki/Delta-v_budget (spiegazione (Delta v))
3. https://en.wikipedia.org/wiki/Tsiolkovsky_rocket_equation (equazione di Tsiolkovsky)
4. https://en.wikipedia.org/wiki/Spacecraft_propulsion (velocità gas propellenti )
5. http://ed-thelen.org/rocket-eq.html (derivazione dell'equazione di Tsiolkovsky)
6. https://en.wikipedia.org/wiki/Gravity_assist (da dove è tratto il viaggio Voyager2)
7. http://www.planetary.org/blogs/guest-blogs/2013/20130926-gravity-assist.html (che riporta numerose traiettorie in animazione)
8. http://www.gravityassist.com/IAF1/Ref.%201-85.pdf (articolo NASA di Minovich)
9. http://www.gravityassist.com/IAF3-2/Ref.%203-140.pdf
10. http://www.adrc.iastate.edu/files/2012/05/Gravity-Assist-Preliminary-Research.pdf
11. http://www.ieec.cat/hosted/web-astro04/notes/gravity.pdf
12. https://solarsystem.nasa.gov/basics/bsf13-1.php (sito NASA che descrive le problematiche e l'evoluzione di sistemi di controllo e simulazione della navigazione spaziale)

File Excel allegato (versione online)

Fai click sull'icona in basso a destra per visualizzarlo in una scheda separata.

Scarica il file Excel.