vuoi
o PayPal
tutte le volte che vuoi
La statistica. Sai ched' e' la statistica? E' 'na cosa/ che serve pe' fa' un conto in generale/ de la gente che nasce, che sta male,/ che more, che va in carcere e che sposa.
Ma pe' me la statistica curiosa
e' dove c'entra la percentuale,
pe' via che, li', la media sempre eguale
puro co' la persona bisognosa.
Me spiego: da li conti che se fanno
seconno le statistiche d'adesso
risurta che te tocca un pollo all' anno:
e, se nun entra ne le spese tue,
t'entra ne la statistica lo stesso
perche' c'e' un antro che ne magna due.
Trilussa (Carlo Alberto Salustri), 1871-1950
INTRODUZIONE
A quei tempi mangiare un pollo all'anno era già segno di un certo benessere.
Trilussa se la prende con la statistica, con le percentuali e con il concetto di media. Certo le licenze poetiche sono preziose e stimolanti, ma per spezzare una lancia in favore dei numeri e della matematica va detto che la statistica oltre al concetto di media prevede anche indici di dispersione attorno ad essa (Es. Scarto quadratico medio) ed indici di disuguaglianza (Es. Coefficiente di Gini).
Anche oggi per consulenti aziendali ed esperti finanziari mettono in guardia dall'uso della Statistica per prevedere sviluppi futuri: "Programmare esiti futuri sulla base della statistica come guidare un'auto che avanza nella nebbia guardando lo specchietto retrovisore!".
Di questo si vuole scrivere, delle situazioni nebbiose, di quando l'ignoranza sui possibili scenari futuri ci impedisce anche di ipotizzare (magari in base alle statistiche passate) le probabilità di accadimento degli scenari stessi. Eppure vedremo che gli strumenti base della statistica: Media (si chiamerà Valore Atteso), Scarto, Minimo, Massimo, Differenza ecc. sono molto utili per prendere razionalmente decisioni relative anche a scenari futuri di cui non son note le probabilità di accadimento (Situazione di incertezza o di ignoranza). Ecco come la Statistica del pollo di Trilussa può essere tradotto in un problema di scelta, riguardante accadimenti futuri.
Comprate un biglietto che vi permette di scegliere tra due lotterie che hanno la stessa "vincita media attesa".
1° Lotteria. Scenario1: vincete un lingotto d'oro, Scenario2: vincete un lingotto d'oro.
2° Lotteria. Scenario1: vincete due lingotti d'oro, Scenario2: non vincete nulla.
Chiunque sia avverso al rischio sceglierebbe la lotteria 1. Ma sempre così? Una persona indebitata, che potrebbe risolvere tutti i suoi problemi con due lingotti d'oro, ma non con uno, sceglierebbe, forse come ultima spiaggia, la lotteria 2. Una persona serena, "ceto medio" mettiamo che la posta invece che in lingotti, sia 10 o 20 , cioè irrilevante per la sua situazione economica, sceglierebbe forse ancora la lotteria 2.
Inoltre vogliamo ricordare che, con il crescente successo della concezione soggettivistica delle probabilità (Ramsey, De Finetti), la distinzione tra situazioni di rischio (le probabilità di accadimento dei vari scenari sono note) e situazioni di ignoranza (le probabilità di accadimento dei vari scenari non sono note) si andata assottigliando. Si possono sempre stimare, seppur soggettivamente, le probabilità dei possibili esiti (scenari). Pertanto, le tecniche usate in condizioni di rischio, possono essere impiegate anche in situazione di incertezza. Del resto quello che si sempre fatto con il criterio di Laplace (secondo altri di Pascal) che, in mancanza di informazioni, assume la equiprobabilità tra i vari scenari possibili.
La teoria razionale delle decisioni ha radici lontane che si possono far risalire all'economista Adam Smith (Mano Invisibile) al matematico Daniel Bernoulli (Funzioni di utilità a marginalità decrescente) e al filosofo Jeremy Bentham (La massima felicità per il maggior numero di persone possibile); essa stata formalizzata dall'economista Leon Walras (Homo oeconomicus) e poi criticata da vari economisti e psicologi. Tra questi si ricorda Herbert Simon per il quale la decisione non si riduce al mero atto di scelta ma un processo complesso in cui interagiscono attori diversi con diverse risorse disponibili. Secondo Simon la razionalità espressa dagli umani sarà comunque sempre limitata e le decisioni raramente porteranno alla scelta ottimale: spesso bisognerà accontentarsi di una scelta soddisfacente. Per Daniel Kahneman non è possibile costruire oggettivamente (concezione normativa) una teoria razionale delle decisioni; quello che si può fare (concezione descrittiva) è studiare come nella realtà gli uomini prendono le loro decisioni (economia sperimentale o comportamentale). Uno dei principali risultati osservati da Kahneman è che la prospettiva di una perdita viene solitamente pesata negativamente più del doppio di un guadagno della stessa entità. Senza trascurare la validità di queste critiche non si può negare che la teoria economica neo-classica e la scuola della ricerca operativa abbiano sviluppato strumenti molto utili per prendere ragionevoli (se non ottime) decisioni nella pratica quotidiana, privata o aziendale. La ricerca operativa suddivide la teoria delle decisioni in 5 gruppi che principalmente si distinguono sulla base del contesto in cui le decisioni vengono prese:
- situazioni deterministiche (programmazione lineare e non lineare)
- situazioni deterministiche ma con criteri di valutazione multipli
- situazioni competitive (teoria dei giochi)
- situazioni di rischio (sono note le probabilità di accadimento degli eventi possibili)
- situazioni di incertezza o ignoranza (non sono note le probabilità di accadimento degli eventi possibili).
E a questa ultima situazione cui ci si riferisce nel resto dell'articolo.
TEORIA
La vita quotidiana, privata, o più spesso aziendale, ci mette di fronte a situazioni che possono/devono richiedere importanti decisioni. Spesso i risultati di tali decisioni sono esprimibili in termini economici, come ricavo, profitto, costo. E evidente che le nostra eventuale decisione avrà lo scopo di ottimizzare la quantità economica del caso e quindi, ad esempio, a rendere massimo un profitto oppure a rendere minimo un costo. La decisione, abitualmente, si configura come una scelta tra diverse alternative. In taluni, fortunati casi, i risultati delle alternative sono di tipo deterministico: vale a dire che, scelta una alternativa, ne consegue di sicuro un determinato risultato. In tali situazioni non resta che pre-calcolare, in modo pi o meno preciso, il risultato di ogni alternativa e scegliere, di conseguenza, l'alternativa più favorevole.
Ma la realtà in cui viviamo di solito non è così facile. Dopo che abbiamo scelto una alternativa si manifestano spesso dei fattori esterni non controllabili, che possono dar luogo a risultati diversi. Definiamo tali fattori scenari e osserviamo che indipendentemente dalla alternativa prescelta, si possono manifestare un certo numero di scenari, che si escludono reciprocamente tra di loro e sono imprevedibili. Solo uno essi si realizzerà, determinando così il risultato.
Esempi di possibili scenari sono le diverse possibili evoluzioni macroeconomiche di un Paese o di un area (EU, NAFTA), o di una commodity o materia prima (petrolio, manganese, uranio, oro,..).
Tutto questo può essere tradotto in termini matematici, scrivendo una matrice dove le righe sono le alternative (che possiamo governare con le nostre scelte), le colonne gli scenari (da noi non controllabili). Gli elementi della matrice sono i risultati (economici), che ipotizziamo di saper calcolare o comunque stimare a priori.
| Scenario A | Scenario B | Scenario C | Scenario D | |
|---|---|---|---|---|
| Alternativa 1 | -100 | 8 | 18 | 94 |
| Alternativa 2 | -20 | 5 | 26 | 70 |
| Alternativa 3 | 2 | 10 | 16 | 20 |
Prendere una decisione significa scegliere una riga della matrice: il risultato della nostra decisione, imprevedibile, sarà l'elemento della riga corrispondente allo scenario che si realizzerà. La situazione che abbiamo descritto si chiama decisione in condizioni di incertezza (o di ignoranza).
Teniamo presente che in molte situazioni ci viene lasciata l'alternativa zero, che significa rifiutare le nuove alternative proposte e quindi mantenere lo status quo (in pratica significa aggiungere alla matrice una ulteriore riga in cui tutte le celle hanno i valori del payout attuale, costante - eventualmente nullo - o variabile). Questa alternativa va sempre considerata contro le altre. Immaginiamo che nel caso in esame le alternative sono businesses, ciascuno dei quali può portare un determinato profitto oppure una perdita, secondo il tipo di scenario; l'eventuale decisione finale di attenersi all'alternativa zero consiste nel non prendere in considerazione tali businesses ed aspettare che si presentino, in un prossimi futuro, alternative più appetibili.
Tornando al caso generale costituito da diverse alternative e diversi scenari la decisione in condizione di incertezza si presenta talvolta difficile e rischiosa. Dopo un ponderato esame della matrice alternative/ scenari possiamo pure decidere di scegliere l'alternativa zero. Ma non possiamo certo pensare di fare sempre questa scelta. Se tutti si fossero sempre comportati così saremmo ancora all'età della pietra!
Ricordiamo che una delle responsabilità del manager di una azienda - privata o pubblica - è quella di prendere decisioni, spesso in condizioni di incertezza. Se non decide l'occasione offerta dalle alternative può scadere. Se tarda a decidere un concorrente più svelto e intraprendente può cogliere l'opportunità, lasciando il manager e la sua azienda a mani vuote.
Tutto quanto detto finora è sufficiente a far capire quanto è importante questo argomento.
Numerosi studiosi si sono ingegnati a sviluppare dei metodi per aiutare la decisione. In particolare vogliamo porre in evidenza i seguenti possibili approcci al problema:
Criterio di Pascal (o di Laplace o della equiprobabilità)
È forse il più evidente ed il più naturale criterio di scelta per qualunque decisore: facciamo la media aritmetica tra i 4 Scenari possibili e scegliamo l'alternativa che ha la media più alta. Nell'esempio riportato sopra:
Alternativa 1: (-100 + 8 + 18 + 94)/4 = 5
Alternativa 2: (-20 +5 + 26 + 70)/4 = 20.25
Alternativa 3: (2 +10 +16 +20)/4 = 12
Dunque la scelta cade sulla Alternativa 2.
Questo criterio di scelta è stato per la prima volta formulato da Laplace, ma molti lo intestano a Pascal in quanto lui è stato il primo a definire la probabilità come: il rapporto tra i casi favorevoli e quelli totali, quando tutti gli eventi possibili sono equiprobabili. Il criterio mutuato dalle decisioni in condizioni di rischio (cioè quando le probabilità di accadimento degli eventi sono note). In quella situazione massimizzare il valore atteso significa massimizzare la somma del prodotto dei risultati per le rispettive probabilità di accadimento, Somma (Xi*Pi). Poiché nel nostro caso, di ignoranza, assumiamo equiprobabilità degli eventi (nell'esempio sono 4, dunque la probabilità per ciascuno 0.25) il valore atteso coincide semplicemente con la media aritmetica sopra calcolata. Questo criterio stato criticato perché non tiene abbastanza conto dei rischi che si possono correre (ed abbiamo visto che secondo Kahneman le perdite fanno male più che doppio, rispetto al piacere dei guadagni). Ad esempio quale decisore sceglierebbe l'Alternativa 2 se fosse disponibile una Alternativa 4 che garantisce con certezza un risultato di 20.25 per ogni Scenario? Chi si assumerebbe il rischio, tra l'altro con probabilità sconosciuta, di una perdita di 20 (Scenario A, Alternativa 2)?
Criterio di Wald (o criterio pessimistico)
Forse per reagire alle critiche rivolte al criterio precedentemente illustrato, l'economista austriaco Abraham Wald ha pensato di cautelarsi rispetto al risultato peggiore (Massimizzare il risultato peggiore):
Risultato peggiore Alternativa 1: -100
Risultato peggiore Alternativa 2: -20
Risultato peggiore Alternativa 3: 2
Dunque la scelta cade sulla alternativa 3 che presenta, nello scenario peggiore, un modesto risultato positivo (+2), ma almeno non negativo. Il criterio di Wald, benché formulato molto prima che Kahneman facesse le sue indagini sperimentali sulla paura provocata dalle perdite, sembra conseguenza delle sue osservazioni. Molti studiosi lo hanno per ritenuto eccessivamente pessimistico. Perché mai gli stati di natura, o se volete l'incertezza, dovrebbe portarci sempre ai risultati peggiori? Un atteggiamento così difensivo è giustificato solo quando gli scenari sono pilotati da un avversario intelligente. Infatti il criterio del Max Min (o del Min Max per l'altro giocatore) è stato formulato per la prima volta da Von Neumann e Morgenstern che si occupavano di strategie competitive per i giochi a somma zero. Una giustificazione del criterio di Wald, per le decisioni contro una natura incerta, la troviamo in Nicol Machiavelli che più di 500 anni fa scriveva:
...Né creda mai alcuno poter sempre pigliare partiti sicuri, anzi pensi a prenderli tutti dubii; perché si truova questo nell'ordine delle cose, che mai non si cerca fuggire uno inconveniente che non s'incorra in un altro; ma la prudenza consiste in saper conoscere la qualità delli inconvenienti e pigliare il meno tristo per buono.
Criterio ottimistico
Questo criterio speculare a quello di Wald e pertanto pecca di eccesso di ottimismo.
Risultato migliore Alternativa 1: 94
Risultato migliore Alternativa 2: 70
Risultato migliore Alternativa 3: 20
In rete circola un aforisma sul pensiero positivo:
Its ok to take risks: if you win you'll be happy, if you loose, you'll be wise.
Il criterio non ha mai avuto particolare seguito o giustificazione, esso è principalmente noto per essere un ingrediente del criterio di Hurwicz illustrato nel seguito.
Criterio di Hurwicz (correggere il pessimismo).
Per l'economista Leonid Hurwicz è necessario correggere il criterio di Wald con una certa dose (
Nell'esempio, secondo le indicazioni di Kahneman, il peggio stato pesato più del doppio rispetto al meglio (meglio:
| Ottimistico Max | Pessimistico Wald Min | Hurwicz 0.3*Ott.+0.7*Pess. | |
|---|---|---|---|
| Alternativa 1 | 94 | -100 | -41.80 |
| Alternativa 2 | 70 | -20 | 7.00 |
| Alternativa 3 | 20 | 2 | 7.40 |
Secondo Il criterio di Hurwicz, con un coefficiente di ottimismo pari a 0.3, La scelta cade sulla Alternativa 3 (risultato economico: 7.40) che supera di poco l'alternativa 2 (risultato economico: 7).
Il criterio di Hurwicz stato criticato perché non mette in conto i risultati intermedi tra l'alternativa migliore e la peggiore. Questa critica è tanto più valida quanto maggiore è il numero delle alternative disponibili al decisore.
Criterio di Rob (pesare la media con il risultato peggiore).
Secondo uno dei due autori di questo articolo, la critica al criterio di Hurwicz può essere superata sostituendo il valore migliore (Ottimistico) con il valore Medio. In questa maniera tutti i valori delle varie alternative vengono rappresentati adeguatamente. Inoltre il valore peggiore (pessimistico), quello più paventato dai decisori che non amano il rischio, viene pesato due volte: nella media e nel valore pessimistico. Si deve inoltre osservare che un valore sufficientemente alto del risultato peggiore garantisce che tutti gli altri valori sotto la media non siano inferiori ad esso. Questo criterio ha il pregio di poter essere applicato anche nelle decisioni in presenza di rischio (probabilità note) e nelle decisioni multi obiettivo (vedi in Bibliografia R. Chiappi: Project Management, Problem Solving, Decision Making). Esso inoltre può essere utilizzato nelle valutazioni macroeconomiche che tendono a stabilire un compromesso tra crescita economica e riduzione della povertà.
| Media Max (0.7) | Pessimistico Wald Min (0.3) | Rob | |
|---|---|---|---|
| Alternativa 1 | 5 | -100 | -26.5 |
| Alternativa 2 | 20.25 | -20 | 8.18 |
| Alternativa 3 | 12 | 2 | 9 |
Secondo Il criterio di Rob, l'alternativa migliore è ancora l'alternativa 3 come per il criterio di Hurwicz. E per da notare che questi due criteri si differenziano maggiormente quanto maggiore è il numero delle alternative: tutte sono considerate da Rob, solo le estreme da Hurwicz.
Criterio della Media - Scarto (detrarre dalla media una quota dello scarto).
In Statistica lo Scarto Quadratico Medio è definito come la radice quadratica della varianza e la varianza è definita come la media delle differenze al quadrato tra ciascun dato e il valor medio. Per meglio intenderci calcoliamo la:
Varianza della Alternativa 1 = [math][(-100 -5)^2 + (8 5)^2 + (18 5)^2 + (94 5)^2]/4 = 4781[/math]
Scarto della Alternativa 1 =
In generale se invece di 4 dati se ne hanno n, la formula : Scarto =
Quanto più è alto lo Scarto quadratico medio di un insieme di dati tanto maggiore è la dispersione dei dati attorno alla media. Se tutti i dati (Xi) coincidessero con la media lo scarto sarebbe nullo. Nella situazione di presa di decisioni ci significherebbe operare in un contesto deterministico senza alcun timore per le incertezze o i risultati peggiori. L'idea dunque di creare un indice che detragga dal valor medio una quota dello scarto che misura il rischio insito nella alternativa. Perché una quota? Gli esperti hanno osservato che bisogna paventare solo gli scostamenti negativi dalla media e non quelli positivi. Suggeriscono dunque di detrarre dalla media (ad esempio) circa lo 0.5 dello Scarto.
| Media | Scarto | Media 0.5 Scarto | |
|---|---|---|---|
| Alternativa 1 | 5 | 69.14 | -29.57 |
| Alternativa 2 | 20.25 | 33.02 | 3.74 |
| Alternativa 3 | 12 | 6.78 | 8.61 |
Ancora una volta la alternativa 3 risulta la prescelta in accordo con il criterio di Hurwicz e di Rob, in generale per, anche questi tre criteri possono fornire risultati diversi.
Criterio di Savage (ridurre il rimpianto rispetto a quello che potrebbe accadere).
Negli ultimi 20 anni l'economia comportamentale, quella emotiva e quella sperimentale hanno a lungo insistito sulla importanza dello stato emotivo del decisore al momento della scelta. Uno delle emozioni più indagate da queste discipline è il rimpianto (Regret Theory). Illustriamo la tematica prendendo come esempio due decisori che hanno investito in titoli:
Il decisore 1, dopo un anno constata che il suo titolo è salito del 3%, osserva poi che tutti gli altri titoli che aveva preso in considerazione hanno avuto una crescita uguale od inferiore al 3%.
Il decisore 2, dopo un anno constata che il suo titolo è salito del 5%, osserva per che molti degli altri titoli da lui considerati hanno registrato un rendimento superiore, uno addirittura arrivato al 10%.
Quale dei due decisori si sentir più soddisfatto? Secondo la teoria razionale delle decisioni il secondo che ha ottenuto un 2% in più rispetto al primo. Secondo l'economia sperimentale il primo. Egli infatti ha un rimpianto nullo mentre il secondo decisore ha un rimpianto di 5 derivante dal fatto di non aver scelto il titolo che cresciuto del 10%. (Nell economia comportamentale si parla molto di effetto di ancoraggio o effetto di incorniciamento).
Gi negli anni 50 dello scorso secolo Jimmie Savage, un matematico e statistico che ha lavorato con Von Neumann e De Finetti, aveva formulato un criterio, per le decisioni in condizioni di incertezza, tendente a ridurre il rimpianto che a posteriori si sarebbe potuto provare come conseguenza del verificarsi di un evento. Il rimpianto si calcola con la seguente formula: Massimo di uno Scenario (colonna) - valore della cella in esame. Come esempio calcoliamo i rimpianti dello Scenario A:
Alternativa 1 = Max (-100, -20, 2) (-100) = 2 + 100 = 102
Alternativa 2 = Max (-100, -20, 2) (-20) = 2 + 20 = 22
Alternativa 3 = Max (-100, -20, 2) 2 = 2 - 2 = 0
Procedendo analogamente al calcolo per gli altri scenari si ottiene la Tavola sottostante in cui nella ultima colonna sono riportati i rimpianti massimi per ciascuna alternativa. Lalternativa prescelta dunque la N 2 che presenta un rimpianto di solo 24 (rispetto al 102 e 74) delle altre.
| Tavola Rimpianti | Scenario A | Scenario B | Scenario C | Scenario D | Min Max (regret) |
|---|---|---|---|---|---|
| Alternativa 1 | 102 | 2 | 8 | 0 | 102 |
| Alternativa 2 | 22 | 5 | 0 | 24 | 24 |
| Alternativa 3 | 0 | 0 | 10 | 74 | 74 |
Il criterio di Savage è considerato meno pessimistico di quello di Wald in quanto lavora sulle differenze (tra Massimo e valore corrente) invece che sui valori assoluti.
Criterio delle eccedenze (premiare il surplus rispetto al peggio che può accadere).
Questo criterio rappresenta, in un certo senso, lo speculare del criterio di Savage in quanto consiste nel sottrarre da ciascun valore il minimo (colonna) dello scenario corrispondente. Per lo Scenario A si trova:
Alternativa 1 = -100 - Min (-100, -20, 2) = -100 (-100) = 0
Alternativa 2 = -20 - Min (-100, -20, 2) = -20-(-100) = 80
Alternativa 3 = 2- Min (-100, -20, 2) = 2 (-100) = 102
Analogamente si calcolano i valori per gli altri Scenari. Nell'ultima colonna sono calcolate le eccedenze minime per ciascun alternativa. La scelta cadrà su quella alternativa che ha la Massima eccedenza Minima.
Essendo, nel nostro esempio Max Min (eccedenze) sempre uguale a zero le alternative risultano indifferenti/equivalenti.
| Tavola Eccedenze | Scenario A | Scenario B | Scenario C | Scenario D | Max Min (ecced.) |
|---|---|---|---|---|---|
| Alternativa 1 | 0 | 3 | 2 | 74 | 0 |
| Alternativa 2 | 80 | 0 | 10 | 50 | 0 |
| Alternativa 3 | 102 | 5 | 0 | 0 | 0 |
Questo criterio, che fornisce sovente risultati d'indifferenza, risulta essere tra quelli meno utilizzati nella pratica operativa degli individui e delle aziende, è comunque ben descritto nel testo di Arcaini e Cordone, citato in bibliografia.
CODICE VISUAL BASIC PER EXCEL
Uno degli autori ha messo a punto (file EXCEL allegato) un semplice software scritto in Visual Basic per applicare i diversi criteri ad esempi di decisione in condizioni di incertezza per il caso di massimizzazione del pay-off. Per usarlo occorre inserire i dati nella zona gialla ottenendo i risultati nell'area azzurra. Notiamo che i risultati presentano diverse colonne, corrispondenti ad eventuali diverse alternative che il criterio della riga in oggetto considera equivalenti. Esiste uno Sheet vuoto, che può essere duplicato per risolvere nuovi problemi di eventuale interesse del lettore.
PROBLEMI
Di seguito sono presentati quattro problemi, di natura completamente diversa, un paio piuttosto complessi, per evidenziare come si possono schematizzare e risolvere casi pratici che si possono presentare nella attività di lavoro.
Caso 1: Le conseguenze di un incendio
Nella notte del 12 settembre un piccolo incendio devasta una sezione di impianto nella fabbrica di Giorgio Rossi, imprenditore alimentare. La fabbrica situata nella zona industriale e la sezione danneggiata è situata vicino ai confini di un'altra piccola fabbrica appartenente a Federico Bianchi. Una veloce indagine condotta dai tecnici di Rossi porta alla conclusione che la causa dell'incendio è stata una fuga di gas infiammabile dalla fabbrica vicina. Rossi si rende conto che una possibile concausa dell'incendio è dovuta agli impianti elettrici della sezione, non completamente a norma. Tuttavia Rossi ritiene giusto richiedere un indennizzo, almeno parziale alla fabbrica vicina, dal momento che i danni sono notevoli.
Dopo alcune riunioni con i suoi tecnici ed i legali Rossi evidenzia tre possibili alternative per ottenere un rimborso:
- Trattativa diretta con Bianchi. Presumibilmente richiederebbe diverse perizie, riunioni, discussioni. Tempo stimato: sei mesi.
- Azione legale. Tempo richiesto alcuni anni. Rossi è consapevole che in caso di sconfitta il payout potrebbe essere negativo, dovendo egli pagare le sue spese legali ed eventualmente quelle della controparte, se così decidesse il giudice civile.
- Rilevare la fabbrica di Bianchi. E noto che piuttosto antiquata. Il proprietario, ormai vecchio, non è interessato a modernizzarla per renderla competitiva. Si sa che Bianchi è già in trattativa da lungo tempo per venderla. Rossi, da parte sua ha un progetto di ampliamento della sua fabbrica, da realizzare fra cinque anni. Anticipando il progetto potrebbe utilizzare la centrale termica di Bianchi e forse qualche apparecchiatura del suo impianto. Rossi pensa di poter convincere Bianchi a concedergli un indennizzo dei danni, come sconto sul prezzo di vendita della fabbrica.
- Le tre alternative si auto-escludono a vicenda. Infatti l'azione legale deve essere intentata entro una settimana: dopo entra in vigore una nuova legge che renderebbe molto difficile la vittoria in campo legale. La proposta di acquisto della fabbrica si deve concretizzare entro un mese, poi si rischia di veder sfumare la possibilità.
- Rossi si rende conto che l'ammontare dell'indennizzo ottenibile dalle tre alternative può essere alquanto variabile essendo condizionato da fattori esterni imprevedibili, che prefigurano diversi scenari. Le sue stime conducono alla seguente matrice alternative/scenari:

Gli elementi della matrice sono gli indennizzi ottenibili, in migliaia di .
In questa spiacevole situazione Bianchi non può rinunciare all'azione, vale a dire scegliere l'alternativa zero. Utilizzando l'applicazione Visual Basic si ottengono i risultati sotto riportati:
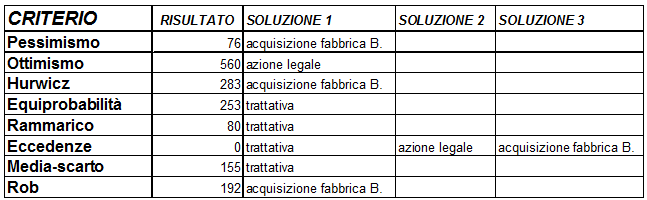
Che potremmo così commentare: Trattativa e Acquisizione della fabbrica di Bianchi sono egualmente raccomandabili. Tuttavia il metodo meno impegnativo è la trattativa, mentre l'acquisizione comporta l'anticipo di un grande investimento, che ovviamente comporta notevoli impegni/problemi finanziari. Da notare che il criterio Eccedenze prevede le tre alternative come egualmente favorite.
Caso 2: Problema del commerciante di pesce
Il testo una adattamento del problema Olivetti citato in bibliografia.
Gino è un commerciante di pesce in una grande città di mare. Ha un bel negozio in centro ed una clientela affezionata. Sanno che il suo pesce molto fresco. Proviene dai piccoli pescherecci che ogni notte gettano le reti al largo della zona. La notte scorsa la pesca stata un po inconsueta. E Gino trova disponibile un solo tipo di pesce. Una cassetta di pesce supponiamo che contenga a circa 10 kg - gli costa 200. La potrebbe rivendere a 350. Se resta invenduta la può svendere, a fine giornata, a 100. Sulla base della sua esperienza Gino stima la domanda questo tipo di pesce: potrebbe vendere da una a quattro cassette. La situazione presenta un notevole grado di incertezza. Ovviamente Gino potrebbe anche scegliere l'alternativa zero, vale a dire prendersi un giorno di vacanza. Il problema può essere formalizzato con una matrice, dove le righe (alternative) sono il numero di cassette che Gino può acquistare, gli scenari (colonne) sono la domanda, vale a dire il numero di cassette che i clienti acquisterebbero. Il file EXCEL riporta, nello SHEET Commercio pesce, la matrice del guadagno(lordo) ottenibile. La matrice è stata costruita con facili calcoli (sostanzialmente guadagno = ricavo - costo) con le formule scritte nelle celle. Ed anche riportata qui sotto.

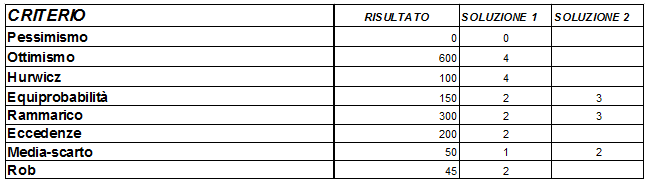
Il codice Visual Basic fornisce le soluzioni per i diversi criteri. L'alternativa preferibile, cioè quella prescelta da 5 criteri degli 8 criteri disponibili (nella tabella seguente i numeri riportati nelle colonne SOLUZIONE rappresentano il numero di cassette acquistate), è l'acquisto di due cassette, che, secondo la matrice, comporterebbe, se entrambe vendute, un guadagno lordo di 300. Il netto sarebbe ovviamente alquanto inferiore, dovendo Gino coprire i costi (affitto, energia elettrica, acqua,) e le diverse tasse e imposte. Alterative nettamente meno favorite sono la compra-vendita di 3 e 4 cassette rispettivamente.
Caso 3: Alternative di sostituzione impianti in una industria grafico-cartotecnica.
Premessa: Ottimizzazione (minimizzazione) dei costi.
La teoria razionale delle decisioni è stata spesso criticata, negli ultimi decenni, perché accusata di perseguire l'efficienza: cioè il profitto dei capitalisti. Di fatto qualunque ospedale, scuola, ente pensionistico, ecc. dovrebbe, a parità di servizi erogati, cercare di minimizzare i propri costi. Non farlo significa distruggere il valore della collettività, ottenuto attraverso il prelievo fiscale.
Da un punto di vista metodologico minimizzare i costi, rispetto a massimizzare i guadagni, può apparire un cambio di paradigma nelle funzioni e nei codici, come quello qui utilizzato (Visual Basic Excel). In realtà la matematica ci insegna che minimizzare una funzione equivale a massimizzare la stessa funzione cambiata di segno: min f(x) = Max[-f(x)]. Si può con questo esempio verificare che la nostra applicazione VBa, progettata per massimizzare i profitti, funziona anche per minimizzare i costi, purché questi siano introdotti come valori negativi. Come esempio ci si avvarrà di un caso aziendale di sostituzione d'impianti in cui le due alternative portano ad eguali ricavi e pertanto ci si riduce ad un problema di minimizzazione dei costi.
Descrizione e soluzione del Caso
Tre laureandi in ingegneria, nell'ambito della loro tesi "La scelta degli investimenti" stanno svolgendo, negli anni 70, presso un poligrafico del centro Italia uno stage, di un paio di mesi, per indicare la miglior scelta di sostituzione di vecchie macchine (3 offset e 3 autoplatine) ormai usurate. Gli studenti dopo aver avuto il quadro dell'azienda dal direttore generale, sono ricevuti dal direttore della produzione, il direttore amministrativo, da quello del marketing e da quello della ricerca. Dai colloqui emerge l'opportunità di considerare due possibilità alternative che si differenziano, non per la capacità produttiva che è uguale, ma per la capacità di gestire variazioni nella entità media delle tirature richieste dalle commesse affidate dai clienti. Le alternative sono:
- Acquisto di una linea composta da tre offset quadricolori e tre autoplatine (macchine piccole, che mediamente permettono di stampare e tagliare/piegare, 8 astucci per foglio)
- Acquisto di una linea composta da due offset quadricolori e due autoplatine (macchine grandi, che mediamente permettono di stampare e piegare 12 astucci per foglio)
Per entrambe le alternative dovranno essere computate due tipologie di costi:
A) costi che non variano con la tiratura media delle commesse:
- Costi di acquisto e installazione delle macchine;
- Costi di manutenzione ordinaria e straordinaria;
- Costi di lavorazione (manodopera, energia elettrica e materiali di consumo);
- Costi del cartone perduto per gli sfridi.
B) costi che variano con la tiratura media delle commesse:
- Costi di attrezzaggio offset (manodopera, inchiostro, lastre);
- Costi di attrezzaggio autoplatine (manodopera, fustelle);
- Costo dei fogli perduti in avviamento/lavorazione.
Il passo successivo consiste nella attualizzazione (vedi in bibliografia: Marco M. e Roberto C.) di tutti i costi:
- I costi di tipo 1) devono essere attribuiti all'istante 0.
- I costi di tipo 2) avvengono sia annualmente (manutenzione ordinaria) sia in anni specifici (manutenzione straordinaria).
- I costi di tipo 3) e 4) avvengono annualmente.
- I costi di tipo 5), 6), 7) avvengono annualmente e variano con l'entit media, e incerta, delle tirature ordinate dai clienti.
La tabella e il grafico riportati sotto rappresentano i costi totali attualizzati per le macchine grandi (linea 2+2) e per le piccole (linea 3+3). Sulle ascisse sono riportate le tirature in centinaia di migliaia di astucci e sulle ordinate i costi attualizzati in milioni di lire. A destra della tabella, media e scarto dei costi totali attualizzati.
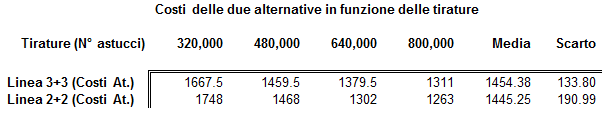
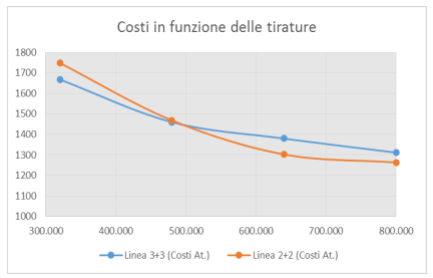
L'osservazione del grafico mostra che, per tirature basse delle commesse, sono convenienti le tre linee di macchine piccole (3+3), mentre per tirature medie e alte sono convenienti le macchine grandi (2+2). Inoltre si può osservare che le macchine grandi hanno una maggior variabilità dei costi al variare delle tirature. Dunque ci aspettiamo per esse (e la tabella sopra riportata lo conferma) uno scarto quadratico medio maggiore.
Nella tabella sottostante sono riportati i risultati (costi come profitti negativi) della applicazione dei vari criteri, in maniera di poter mantenere la stessa ottica massimizzante e poter utilizzare la stessa routine Visual Basic.

L'analisi dei criteri mostra, come già intuito osservando il grafico, una quasi parità in termini di valore atteso (valore medio) e una sensibile differenza in termini di scarto. Tutti i criteri sono favorevoli alla linea di macchine piccole (3+3) con l'eccezione del criterio ottimistico e di quello delle eccedenze (ancora una volta parità tra le scelte). A parere degli scriventi questi due ultimi criteri appaiono come i meno giustificabili razionalmente.
Fattori a favore delle macchine piccole rilevanti per la scelta, ma difficilmente quantizzabili:
- Le maestranze del poligrafico sono da tempo abituate a gestire macchine piccole (tre stampatrici pi tre fustellatrici).
- Le macchine piccole sono più flessibili e richiedono minori tempi di attrezzaggio.
- I casi di guasto a una linea (blocco di un terzo della produzione, contro blocco di metà della produzione) sono meglio gestibili e meno penalizzanti.
Solo se in futuro le strategie di marketing del poligrafico si orienteranno verso pochi grandi clienti che ordinano commesse di grande tiratura, sar conveniente orientarsi verso le linee 2+2 di macchine grandi.
Un estratto del lavoro dei tre neolaureati, stagisti presso il poligrafico, è stato pubblicato nel 1972 (vedi bibliografia) su Italia Grafica organo ufficiale dell'associazione nazionale italiana industrie grafiche cartotecniche e trasformatrici.
Il relatore della tesi, incaricato di Ricerca Operativa al Politecnico di Milano così scriveva nella presentazione: "In questi ultimi anni si è andato estendendo l'uso dei metodi quantitativi per la soluzione di vari problemi di organizzazione e gestione aziendale. In particolare i modelli della Ricerca Operativa e i relativi metodi di soluzione sono stati impiegati dapprima in relazione a problemi di pianificazione della produzione e di gestione delle scorte. Più tardi il loro uso è stato esteso ad alcuni aspetti finanziari e di marketing... L'accurata analisi, qui presentata, mette in luce una sostanziale parità tra le due soluzioni in termini di costo atteso che permette di basare la decisione su una serie di fattori di difficile quantizzazione".
Dopo pochi anni il poligrafico procedette, progressivamente, alla sostituzione delle vecchie macchine con una linea, 3+3 di macchine piccole. La scelta fu vincente in quanto nei successivi 10 anni Il 68% delle commesse fu inferiore al break-even point (tirature di circa 500.000 astucci per commessa. Vedi grafico) e solo il 32% super tale livello.
Caso 4: La costruzione di un albergo
Questo Caso ripreso e adattato/modificato dal testo di Kaufmann citato in bibliografia.
Una catena alberghiera sta valutando il dimensionamento, su un terreno di sua proprietà già acquisito all'uopo, di un nuovo albergo. Non avendo a disposizione statistiche sulle presenze medie annue di turisti in quella località i proprietari non hanno ancora deciso se l'albergo dovrà essere equipaggiato con 20, 30, 40 o 50 stanze. La catena ha recentemente assunto un giovane ingegnere esperto di ricerca operativa e tecniche decisionali. Il direttore ha dato l'incarico al suo esperto preventivista di stimare costi e ricavi dell'albergo in funzione del numero medio di camere occupate nell'anno. Per semplificare il problema si è assunto che nell'anno la domanda dei clienti potrà portare ad occupare mediamente: 0 o 10 o 20 o 30 o 40 o 50 camere. Purtroppo non si può stimare neanche con quale probabilità si verificheranno le possibili domande di alloggio, pertanto, se si sono costruite poche stanze e la domanda media è sostenuta, si dovranno mandare indietro dei clienti. Al contrario, se si sono costruite molte stanze e la domanda è bassa, molte stanze resteranno vuote. E evidente che il progetto presenta molte incertezze causate dalla completa ignoranza sulle richieste di alloggio dei turisti nei prossimi anni. Vista la natura del problema il direttore dice al preventivista di avvalersi dell'ingegnere per preparare dei prospetti che possano supportare la proprietà a prendere la decisione più appropriata. In un paio di giorni il preventivista, che molto esperto, prepara la seguente lista di costi e ricavi annui e la mostra all'ingegnere.
Costi annui fissi:
Gestione e manutenzione del terreno, quota fissa delle spese di manutenzione e riparazioni dell'albergo, un portiere notturno, stipendio di un tecnico per la manutenzione. Totale 25,500.
Costi annui fissi, proporzionali al numero di camere costruite:
Quota annua di ammortamento della Costruzione e del mobilio delle stanze, una domestica per ogni 10 stanze, spese di manutenzione e riparazione proporzionali al numero delle camere, assicurazioni anti incendio ed altro proporzionali al numero delle camere. Totale: 95,500 (per 20 stanze), 143,250 (per 30 stanze), 191,000 (per 40 stanze), 238,750 per (per 50 stanze).
Costi annui variabili con il numero medio di stanze occupate previste:
Pulizia stanze e lavaggio biancheria, elettricità, gas, acqua, climatizzazione. Totale 0 (per nessun cliente), 36,000 (per 10 stanze occupate), 72,000 (per 20 stanze occupate), 108,000 (per 30 stanze occupate), 144,000 (per 40 stanze occupate), 180,000 (per 50 stanze occupate).
Ricavi annui variabili con il numero medio di stanze occupate previste:
In accordo con l'ufficio locale del turismo, con le tariffe medie stagionali, e con la categoria dellalbergo (si prevede un quattro stelle) i ricavi annui possono essere cos sintetizzati: 0 (per nessun cliente), 219,000 (per 10 stanze occupate), 4382,000 (per 20 stanze occupate), 657,000 (per 20 stanze occupate), 876,000 (per 40 stanze occupate), 1095,000 (per 50 stanze occupate).
Il giovane ingegnere resta perplesso. Riconosce che i dati sono, completi, ma per poter applicare i criteri decisionali che ha studiato all'università, deve riportarli ad una più consueta forma tabellare. Il preventivista e l'ingegnere decidono di lavorare insieme in modo di riclassificare i dati come se si trattasse di 4 progetti diversi (20,30,40,50 Stanze costruite) tenendo anche conto degli eventuali clienti respinti o delle camere rimaste vuote. Dopo due ore di lavoro ecco il risultato ottenuto con l'aiuto tabella elettronica:
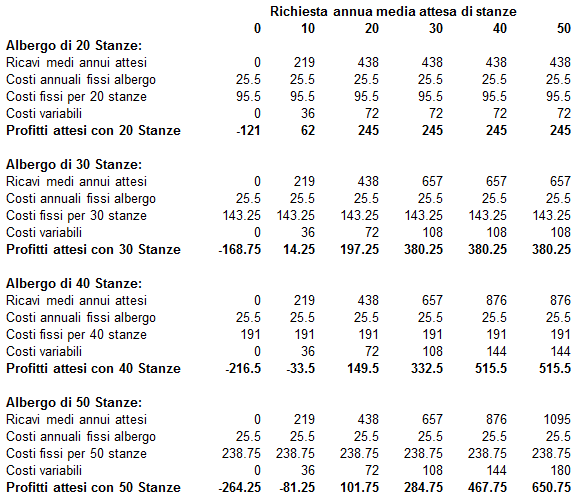
L'ingegnere, soddisfatto per tutto l'aiuto avuto, ringrazia il collega anziano e gli mostra la tabella: Alternative (Stanze costruite) /Scenari (Profitti presunti) che intende utilizzare per la sua Decision Analysis:
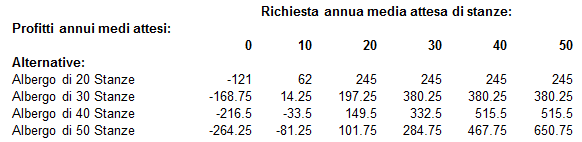
Da questa tabella l'ingegnere ottiene facilmente gli indicatori proposti dalla Ricerca Operativa/Analisi delle decisioni e da noi illustrati nelle pagine precedenti:
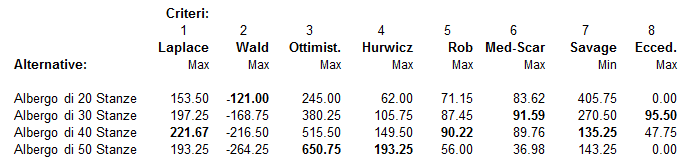
Soddisfatti, il preventivista e il giovane ingegnere vanno dal direttore proponendogli di suggerire alla proprietà la costruzione di un albergo di 40 stanze. La decisione giustificata dal fatto che il preventivista e il giovane ingegnere pongono maggior fiducia nei criteri di Laplace, Savage e Rob. Se le condizioni finanziarie della catena alberghiera (qui non prese in considerazione) suggeriscono un profilo più basso (magari con più rapidi rientri), potrebbe essere meglio ripiegare su un Hotel di 30 Stanze, alternativa per altro suggerito dal criterio Media 0.5 Scarto.
Conclusioni
Da osservatori interessante far notare come le principali teorie/strumenti applicabili di ricerca operativa/analisi delle decisioni siano maturate nel secondo dopo guerra (Cfr. Von Neumann, Dantzig, Khun, Tucker, Roy, Lang, Doig, Wald, Savage, De Finetti, Ramsey, Nash, Aumann ecc.). Per le decisioni in condizioni di incertezza nessun criterio, praticamente utile, è stato proposto dopo gli anni 60, con l'eccezione del criterio di Rob, proposto da uno dei due autori di questo articolo. Negli ultimi 50 anni preziose considerazioni sono invece state fatte dagli economisti/psicologi comportamentali sulla razionalità limitata, le soluzioni soddisfacenti, il dolore del peggio ecc. E per mancato lo studio e la proposta di nuovi criteri in grado di aiutare in modo propositivo/pratico, a prendere decisioni in condizioni di incertezza e con la totale ignoranza delle probabilità di accadimento degli eventi possibili.
BIBLIOGRAFIA
- Kaufmann, Faure Invitation la recherche operationelle, Dunod Paris 1966.
- Divisione Elettronica Olivetti, Elementi di Ricerca Operativa, Dispensa interna 1968.
- Bonetti, Chiappi, Vitale, Il problema della scelta degli investimenti e la ricerca operativa, Italia Grafica, Febbraio 1972.
- M. Motterlini, Economia Emotiva, Rizzoli 2006.
- Arcaini, Cordone, Decisioni in condizioni di incertezza, Universit di Milano 2009.
- Marco M. e Roberto C., Scelta tra investimenti industriali
- R.Chiappi, Project Management, Problem Solving, Decision Making
CASO 1 : INCENDIO ( Il codice è riportato nel modulo Visual Basic ) ( Per far eseguire il codice posizionarsi su questo SHEET)
SCENARI
ALTERNATIVE Tutti i dati sono espressi in Migliaia di €
INSUCCESSO INTERMEDIO SUCCESSO
trattativa 0 280 480
azione legale -40 200 560
acquisizione fabbrica B. 76 160 490 CRITERIO
Hurwicz
Media-scarto
Rob
CRITERIO RISULTATO SOLUZIONE 1 SOLUZIONE 2 SOLUZIONE 3 SOLUZIONE 4 SOLUZIONE 5
Pessimismo 76 acquisizione fabbrica B.
Ottimismo 560 azione legale
Hurwicz 283 acquisizione fabbrica B.
Equiprobabilità 253 trattativa
Rammarico 80 trattativa
Eccedenze 0 trattativa azione legale acquisizione fabbrica B.
Media-scarto 155 trattativa
Rob 192 acquisizione fabbrica B.
CASO 2: COMMERCIO PESCE ( Il codice è riportato nel modulo Visual Basic ) ( Per far eseguire il codice posizionarsi su questo SHEET)
SCENARI = domanda= quantità vendute(cassette)
ALTERNATIVE= quantità acquistate(cassette) 0 1 2 3 4
0 0 0 0 0 0
1 -100 150 150 150 150
2 -200 50 300 300 300
3 -300 -50 200 450 450
4 -400 -150 100 350 600 CRITERIO PARAMETRO VALORE
Hurwicz α 0,5
Media-scarto λ 0,5
Rob β 0,7
CRITERIO RISULTATO SOLUZIONE 1 SOLUZIONE 2 SOLUZIONE 3 SOLUZIONE 4 SOLUZIONE 5
Pessimismo €/cassetta
0 0 Costo acquisto pesce 200
Ottimismo €/cassetta
600 4 Prezzo vendita pesce 350
Hurwicz Prezzo svendita pesce 100
100 4 €/cassetta
Equiprobabilità 150 2 3
Rammarico 300 2 3
Eccedenze 200 2
Media-scarto 50 1 2
Rob 45 2
CASO 3: COSTO RINNOVO IMPIANTI ( Il codice è riportato nel modulo Visual Basic ) ( Per far eseguire il codice posizionarsi su questo SHEET)
SCENARI
ALTERNATIVE Tiratura 320K Tiratura 480K Tiratura 640K Tiratura 800K
Investimento linea 3+3 -1667,5 -1459,5 -1379,5 -1311
Investimento linea 2+2 -1748 -1468 -1302 -1263 CRITERIO PARAMETRO VALORE
Hurwicz α 0,5
Media-scarto λ 0,5
Rob β 0,7
CRITERIO RISULTATO SOLUZIONE 1 SOLUZIONE 2 SOLUZIONE 3 SOLUZIONE 4 SOLUZIONE 5
Pessimismo -1668 Investimento linea 3+3
Ottimismo -1263 Investimento linea 2+2
Hurwicz -1489 Investimento linea 3+3
Equiprobabilità -1445 Investimento linea 2+2
Rammarico 78 Investimento linea 3+3
Eccedenze 0 Investimento linea 3+3 Investimento linea 2+2
Media-scarto -1521 Investimento linea 3+3
Rob -1518 Investimento linea 3+3
