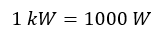Missioni dello stesso programma, nei tre anni successivi, permisero di approfondire indagini e rilevamenti e di portare sulla Terra campioni di minerali lunari.
Dal 1971 hanno inizio, per opera dei russi, le prime stazioni spaziali permanenti in orbita terrestre bassa (LEO); in successive iniziative si giunge nel 1998 all'ISS (Stazione Spaziale Internazionale).
Questo progetto, gradualmente ampliato nel corso degli anni, è tuttora operativo e si avvicendano frequentemente astronauti di diversa nazionalità per eseguire esperimenti di varia natura in assenza da gravità.Dal 1970 sonde russe sono atterrate su Venere per eseguire rilevamenti. Seguirono sonde americane.
Negli anni '60 e '70 russi e americani, dopo diversi tentativi falliti, riuscirono a far atterrare delle sonde automatiche sulla superficie di Marte. Le missioni sono continuate fino al 2016.
Una sonda NASA lanciata nel 2006 ha raggiunto Plutone nel 2016. Le sonde Voyager e Pioneer sono uscite dal sistema solare.
NASA sta sviluppando un progetto per l'invio di una missione umana su Marte, che richiederà qualche decennio per essere attuata.
Dal 1974 esiste il progetto SETI (Search of Extraterrestial Intelligence) con invio e la ricezione di segnali radio nello spazio alla ricerca di forme di vita intelligente extraterrestre: finora nessun risultato.
Il passo successivo che si pone la scienza è l'esplorazione dello spazio lontano: altri sistemi stellari e i relativi pianeti. Da qualche anno è stato possibile individuare, a media distanza, numerosi esopianeti vale a dire pianeti che potrebbero offrire le condizioni utili allo sviluppo di organismi viventi.
Il problema essenziale per tali esplorazioni è la messa a punto di sistemi di propulsione adeguati per viaggi a distanza di alcuni/alcune decine di anni luce.
PROPULSIONE NELLO SPAZIO - STATO ATTUALE
La tecnologia degli Stati più avanzati ha sviluppato mezzi spaziali costituiti da razzi pluristadio anche di grande potenza, ad es. i razzi Saturn (USA) e Soyuz (Russia).Il principio di funzionamento del motore a razzo si basa sulla terza legge della dinamica: all'espulsione dall'ugello con la relativa spinta -S di una massa di gas corrisponde una reazione uguale e contraria S sul razzo. La spinta dei gas si realizza tramite una reazione chimica tra i componenti del propellente che genera gas ad altissima temperatura: attraverso un ugello convergente-divergente l'energia termica viene convertita in energia meccanica. In un precedente articolo (R1) è stata descritta l'equazione fondamentale che correla masse espulse e velocità dei gas. In tal modo si può spingere il razzo fino a una velocità di diversi km/s. Combinando la spinta con un altro stratagemma, denominato effetto fionda, è possibile aumentare ulteriormente la velocità del razzo. Lo stato dell'arte è rappresentato dalla sonda Voyager 1 che dopo 37 anni di navigazione ha lasciato il sistema solare e viaggia nel cosmo alla velocità costante di 17 km/s.
Un miglioramento della spinta del razzo si ottiene con la propulsione ionica (anche detta propulsione elettrica (R2). Il gas, in questo caso Xenon, viene ionizzato ricorrendo all'energia elettrica accumulata da celle solari. Il gas elettricamente carico è fatto passare su di una griglia - posizionata sulla parte finale dell'ugello ed a sua volta caricata elettricamente - che accelera il gas. In tal modo si ottiene un impulso specifico (denominato Isp) di un ordine di grandezza superiore a quello della propulsione chimica. La tecnica è stata applicata a diverse sonde, tra di esse Dawn che ha sorvolato il protopianeta Vesta ed è ora in orbita permanente attorno a Ceres.
PROPULSIONE INTERSTELLARE
Il problema della navigazione interstellare è chiaramente la grandissima distanza che separa tra di loro i sistemi stellari. Sappiamo che la stella più vicina alla Terra è Proxima Centauri, che fa parte di un sistema di tre stelle denominato Alfa Centauri, alla distanza di 4,3 anni luce. Altre stelle recentemente oggetti di studio sono Trappist-1 (a 39 Anni luce) e Kepler-452b (a 1400 anni luce). Queste stelle possiedono uno o più esopianeti, che la scienza è interessata a conoscere da vicino per accertare se possiedono forme di vita organica ed eventualmente potrebbero essere colonizzati nel lontanissimo futuro.Come si può raggiungere uno di questi sistemi stellari per avere informazioni, anche preliminari? Evidentemente con un mezzo spaziale, in prima battuta una sonda - vale a dire una navetta automatica priva di equipaggio- dotata di adeguata velocità. Quanto adeguata? Abbastanza da rendere il viaggio possibile entro qualche anno o poche decine di anni. Perché questo avvenga, è necessario spingere la sonda a velocità luminali, vale a dire raggiungere velocità che sono una frazione significativa della velocità della luce c (che è pari a (3 ast 10^8 m/s)). In pratica sembra ragionevole operare a velocità v compresa tra il 10% e il 25% di c. Come si è visto questo non è neppure lontanamente possibile con la propulsione chimica o ionica. Mentre, in teoria si potrebbe generare propulsione con un'onda elettromagnetica.
AZIONE A DISTANZA DI UN'ONDA ELETTROMAGNETICA
La fisica ci insegna che un raggio elettromagnetico inviato contro una superficie viene in parte assorbito e in parte riflesso. L'interazione del raggio (che può essere rappresentato come un flusso di fotoni) con la superficie genera, per reazione, una debole spinta (vale a dire una forza) S. Se P0 è la potenza del raggio, εr la frazione della potenza riflessa, risulta:[ \begin{equation} S = frac{P_0 (1+epsilon_r)}{c} label{eq1} end{equation} ]
Nel caso (desiderabile) in cui il raggio sia completamente riflesso, si ha ( epsilon_r = 1 ) e quindi ( S = frac{2P_0}{c} )
Per ottenere questo si può usare un foglio di materiale molto sottile (spessore di micron) rivestito da una vernice riflettente oppure un materiale di per sé riflettente, come ad es. l'alluminio. Il raggio elettromagnetico può essere il raggio solare oppure un raggio laser di frequenza e potenza adeguate. Se il raggio è abbastanza potente e l'area della superficie sufficientemente grande, si ottiene una spinta che, se prolungata - in modo continuo o pulsato - per un lungo periodo, risulta adatta a spingere la sonda a grande velocità nello spazio cosmico. Evidentemente la potenza superficiale del raggio non deve essere eccessiva per evitare surriscaldamento o fusione della superficie. Sarà necessario avere un'area superficiale piuttosto grande: una vela.
PROPULSIONE A VELA SOLARE
Un progetto teorico potrebbe fare ricorso alla spinta dei raggi solari. E' stato notato che sarebbe opportuno posizionare una sonda con vela in prossimità del Sole, diciamo ad una distanza pari a quella di Mercurio dal Sole. Si avrebbe allora alla partenza il massimo di spinta da parte dei raggi solari sulla base della ((\ref{eq1})). Dal momento che i raggi solari si diffondono uniformemente nel cosmo secondo superfici sferiche concentriche al Sole, la vela sarebbe costantemente irradiata, in tutta la sua superficie, dai raggi del Sole. Tuttavia la potenza per unità di superficie dei raggi solari decresce con la distanza x dal Sole. Questo riduce la spinta:[ \begin{equation} S = frac{P_0(1+epsilon_r)}{cx^2} label{eq2} end{equation} ]
Inoltre, essendo la spinta S non molto grande, occorre tenere conto anche dell'attrazione gravitazionale solare, che è data dalla legge di gravitazione universale:
[ \begin{equation}F_g = - frac{kmM}{x^2} label{eq3} \tag{3} end{equation} ]
che si oppone alla spinta dei fotoni solari. Dove m e M sono le masse della sonda e del Sole.
In APPENDICE 1 viene riportato in dettaglio lo sviluppo matematico del moto della sonda con un esempio numerico. Qui ci limitiamo a concludere che la velocità della sonda raggiungibile con la propulsione solare è piuttosto modesta, dell'ordine dello zero virgola % della velocità della luce. Il tempo necessario a raggiungere Alfa Centauri è inaccettabile, pari a 12 mila anni. Si deve prendere atto che la propulsione solare, idea certamente interessante, potrebbe trovare valida applicazione nei viaggi all'interno del sistema solare, ma non è adatta per l'esplorazione interstellare.
Un sistema molto più efficiente si ottiene mediante la spinta di un raggio laser che può essere opportunamente dotato di una potenza per unità di superficie di gran lunga superiore ai raggi solari.
PROPULSIONE A VELA LASER
I primi studi di esperti del settore astronautico risalgono ormai agli anni '80. Altri si occuparono dell'argomento negli anni seguenti (R3). Nel 2016 un professore universitario americano, Philip Lubin, ha sviluppato uno studio di dettaglio (R5) che si occupa dei vari e complessi aspetti della vela laser. Una sonda spaziale di piccola massa m, dotata di una vela ripiegata, viene messo in orbita terrestre LEO con un razzo convenzionale (figura sotto).

Mediante opportuni meccanismi la vela viene dispiegata e irradiata con un raggio laser allo stato solido all'Itterbio (Yb) che opera su lunghezze d'onda di 1μm, nell'infrarosso.
Per far questo si assume di disporre di una batteria di numerosi laser sincroni posta sulla Terra su di una superficie abbastanza ampia, ad es. a forma quadrata, con lato dell'ordine del metro o di suoi multipli(100, 1000,10000). In tal modo la potenza risulta scalabile aumentando il numero di laser basati sulla tecnologia esistente. Si può pensare di operare con una potenza complessiva dell'ordine di 100GW. Mediante opportuni sistemi di lenti il fascio laser, operato in modalità pulsata (di potenza P0), viene collimato su di un'area di partenza piuttosto piccola, ottenendo un fascio di raggi paralleli e coerenti, ed inviato nello spazio contro la vela della sonda (come da figura sotto, che ovviamente non è in scala):
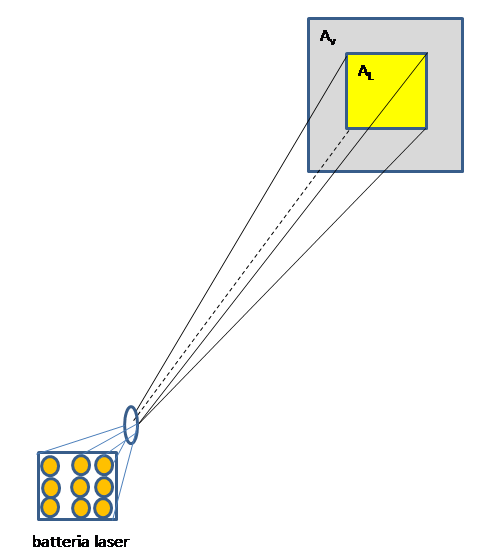
Come è intuibile un fascio luminoso inviato nello spazio si allarga, tuttavia è caratteristico del laser il fatto che la dispersione del fascio è molto contenuta (l'angolo di dispersione è dell'ordine di 10-6 radianti). Il fascio laser che incide sulla vela (la macchia AL, in giallo) copre una parte della vela (di area AV, in grigio). La sonda spinta dal laser si allontana progressivamente e in tal modo la macchia si estende gradualmente fino a coincidere con la superficie totale della vela. Fino allora l'intera potenza P0 del laser agisce sulla vela, che riceve spinta ed accelerazione costanti:
[ \begin{equation} a = frac{F}{m} = frac{P_0(1+epsilon_r)}{mc} label{eq4} \tag{4} end{equation} ]
A distanza superiore la macchia copre l'intera la vela, ma parte del raggio laser fuoriesce dalla vela e la potenza applicata si riduce, così pure la spinta e l'accelerazione.
Notiamo dalla ((\ref{eq4})) che la spinta specifica ottenibile è data da:
[ frac{F}{P_0} = frac{(1+epsilon_r)}{c} approx frac{2}{c} = frac{2}{3 ast 10^8} = 0.67 ast 10^{-8} frac{N}{W} = 6.7 frac{N}{GW} ]
che è molto piccola. Tuttavia se applichiamo una grande potenza (poche centinaia di GW) si può ottenere una spinta F di un migliaio di N. Se la massa della sonda è abbastanza piccola (dell'ordine del kg) si realizza un'accelerazione pari ad un migliaio di g (accelerazione di gravità terrestre). Se quest'accelerazione dura per alcune ore, è più che adeguata per raggiungere velocità luminali.
Per ottenere questo risultato è necessario scegliere opportunamente le caratteristiche della sonda/vela (m, AV, ) e del laser (potenza e lunghezza d'onda λ).
Lo studio, piuttosto completo e dettagliato in tutti gli aspetti della propulsione con vela laser, è riportato in un articolo scientifico molto ampio del prof. Philip Lubin (R5), che contiene anche il modello matematico, semplice ed elegante. Esso consta di un insieme di equazioni algebriche che si risolvono facilmente a cascata.
Un esempio di calcolo di un'ipotetica sonda, provato dall'autore di quest' articolo (descritto in APPENDICE 2), mostra che si potrebbe raggiungere il sistema Alfa Centauri in una trentina di anni, tempo non breve ma abbastanza accettabile.
Il progetto è futuribile e richiede un ulteriore sviluppo delle tecniche di miniaturizzazione dei componenti elettronici e di rilevamento, la messa a punto e sperimentazione di materiali adatti per la vela ed i meccanismi di dispiegamento della vela. Un elemento critico del progetto è la creazione di sistemi di puntamento laser e di controllo/regolazione della vela per fare in modo che il baricentro della spinta laser sulla vela coincida con il baricentro della sonda; diversamente si produrrebbe un momento rotatorio che vanificherebbe la propulsione laser.
INIZIATIVA REALE
Nel 2016 il tycoon russo Yuri Milner ha annunciato uno studio per la costruzione di una leggerissima sonda (nanocraft) con propulsione a vela laser, sulla base delle teorie del prof Lubin. Il progetto (R6), denominato Breakthrough Starshot, finanziato con 100 milioni di USD, si avvale di un team prestigioso: Stephen Hawking (autore della teoria dei buchi neri, il più noto scienziato vivente), Pete Warden (ex direttore di una centro NASA), prof. Avi Loeb (astrofisico di Harvard), prof. Philip Lubin (UC Santa Barbara), Mark Zuckerberg (CEO di Facebook).S'immagina una vela spinta da un laser a impulsi con potenza di 100 GW che impiegherebbe circa 20 anni per andare a destinazione con sorvolo e rilevazione dati di Alpha Centauri. Una prima stima del costo di realizzazione per il solo sistema laser è dell'ordine di 1000 miliardi di USD (pari al 60% del PIL italiano) ai costi unitari attuali. Ovviamente si spera che gli sviluppi tecnologici possano abbattere i costi di almeno un ordine di grandezza. Tempi stimabili: una generazione.
METODI ALTERNATIVI
L'articolo ha descritto il principio fisico e alcuni aspetti dei modelli base che potrebbero servire allo sviluppo di sistemi di navigazione nel cosmo, nel sistema solare ed interstellare, con sonde spinte da raggi. Il vantaggio è evidente: si eviterebbe di trasportare enormi masse di propellente che appesantiscono il mezzo spaziale e danneggiano l'accelerazione. In questo modo si possono raggiungere velocità luminali e il viaggio si realizza in tempi accettabili.
Tuttavia esistono, come è facilmente immaginabile altre idee, basate su principi diversi (R7). Infine può essere interessante riflettere sulle alternative ed i problemi nel caso, molto ipotetico e futuribile, della esplorazione interstellare con equipaggio umano; per questo argomento si rimanda all'articolo (R8). Dove si riportano come possibili rimedi ai lunghissimi tempi di viaggio:
- L'ibernazione
- Le astronavi generazionali
PARADOSSO?
Se infine ci sbarazziamo di tutti i vincoli imposti dalle attuali limitazioni scientifiche/tecnologiche e immaginiamo di disporre di un ipotetico sistema di propulsione che ci permetta la navigazione spaziale a velocità luminali con un'astronave dotata equipaggio, ci troviamo immediatamente ad affrontare l'apparente Paradosso dei Gemelli, che riportiamo di seguito.Supponiamo che un gemello resti a Terra e l'altro parta per un viaggio spaziale di andata e ritorno a velocità luminale costante v, verso un sistema stellare lontano anni luce; al ritorno risulta che il gemello viaggiatore è più giovane dell'altro. Ciò è dovuto al fatto che per il gemello viaggiatore il tempo scorre più lentamente.
Questo apparente paradosso è stato affrontato da molti autori nel corso degli ultimi decenni, sulla base della la Teoria della Relatività. Secondo alcuni il problema andrebbe approcciato ricorrendo alla Relatività Generale (teoria di uso molto complesso), secondo altri si può approssimare oppure risolvere esattamente con la Relatività Ristretta (definita Special Relativity nei Paesi anglosassoni). Quest'ultima può essere vista come una versione della Relatività Generale nel caso molto particolare in cui tutti i sistemi di riferimento sono inerziali, vale a dire sono immobili o si muovono di moto uniforme (i.e. in linea retta a velocità costante).
Una fra le numerose spiegazioni del paradosso si trova in un articolo di Scientific American (R10).
In ogni caso autori diversi giungono con approcci alternativi allo stesso risultato, che si ottiene applicando una delle famose formule di Lorentz (R11, R12) per il moto monodimensionale. La quale correla la durata temporale del viaggio misurata dal gemello viaggiatore ( rispetto alla durata misurata dal gemello sulla Terra :
[ \begin{equation} \tau' = frac{\tau-frac{\beta}{c}L}{\sqrt{1-\beta^2}} label{eq21} \tag{21} end{equation} ]
[ \begin{equation} \beta = frac{v}{c} label{eq22} \tag{22} end{equation} ]
dove: ( 0 lt \beta lt 1 ,,,,,,, v = mbox{velocità} )
Nel caso dei gemelli assumiamo che sia L la distanza percorsa nel viaggio A+R dal gemello viaggiatore.
Notiamo che la durata del viaggio misurata dal gemello sulla Terra vale (\tau = frac{L}{v} ) e quindi ( L = \tau v) che, sostituita nella ((\ref{eq21})), con facili passaggi permette una notevole semplificazione: [ \tau' = \tau \sqrt{1-\beta^2} ]
Pertanto il rapporto delle durate vale:
[ \begin{equation} frac{\tau'}{\tau} = \sqrt{1-\beta^2} label{eq23} \tag{23} end{equation} ]
Questo è davvero interessante, perché il rapporto delle durate non dipende dalla distanza L percorsa. La formula può essere diagrammata:
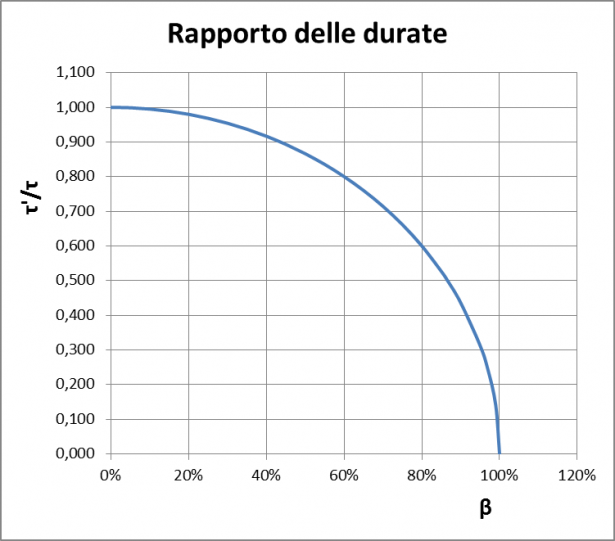
Notiamo che quando v e β tendono a zero il rapporto (frac{\tau'}{\tau}) tende a
Vediamo un esempio: il gemello viaggiatore fa un viaggio A/R verso un esopianeta del sistema stellare Trappist-1, che dista dalla Terra 39 anni luce, a (\beta = 0.866) (vale a dire: ( v = 86.6\%c)). Per questo particolare valore di β con la formula ((\ref{eq23})) si ha (frac{\tau'}{\tau}=0.5). Inoltre risulta che:
[ \tau = frac{2 ast 39}{0.866} = 90, mbox{anni} ]
[ \tau' = 0.5\tau = 45, mbox{anni} ]
In definitiva, se il gemello viaggiatore è partito in giovane età, al ritorno si trova in età da pensione. Mentre il gemello rimasto sulla Terra è scomparso e con lui parenti, amici, conoscenti, colleghi del gemello viaggiatore. Non si tratta di un paradosso, ma della triste realtà. Al sopravvissuto, rimasto solo, resterebbe la soddisfazione di vedere come è cambiata la società terrestre ad un secolo di distanza.
Il file EXCEL-Paradosso riporta i calcoli di dettaglio.
(Fai click sull'icona in basso a destra per visualizzare la cartella di lavoro a pagina intera)
APPENDICE 1 - VELA SOLARE ↑
Come detto in precedenza s'immagina di inviare la sonda, con un razzo convenzionale, abbastanza vicina al Sole - diciamo pari alla distanza media Sole-Mercurio - per sfruttare al massimo la spinta fotonica del Sole. La vela solare è soggetta a due forze di natura solare: quella repulsiva (Fv) dovuta ai raggi (fotoni) solari e quella attrattiva (Fg) della gravitazione. Se immaginiamo di tracciare un asse delle ascisse dal Sole al sistema Alfa Centauri saranno x0 e vo rispettivamente posizione e velocità della sonda al tempo t=0 (figura sotto)
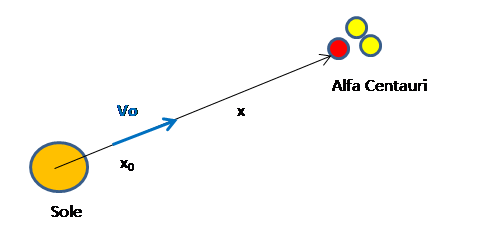
L'equazione del moto della sonda (2° principio della dinamica):
[ \begin{equation} mfrac{dv}{dt} = F_v - F_g = a frac{A}{x^2} - k frac{mM}{x^2} label{eq5} \tag{5} end{equation} ]
Dove: ( A, mbox{è la superficie della vela}, a = 6.38 ast 10^{16} ) (fonte R9) mentre k=costante di gravitazione universale, m=massa sonda, M=massa solare, che sono delle costanti.
Inoltre scriviamo l'equazione che definisce la velocità come derivata dello spazio percorso rispetto è tempo:
[ \begin{equation} frac{dx}{dt} = v label{eq6} \tag{6} end{equation} ]
la ((\ref{eq5})) può essere scritta in modo più compatto ponendo (b = kM = 6.38 ast 10^{16}) e dividendo per
[ \begin{equation} frac{dv}{dt} = frac{a frac{A}{m}-b}{x^2} = frac{frac{a}{\sigma}-b}{x^2} label{eq7} \tag{7} end{equation} ]
dove si è posto (\sigma = frac{m}{A} ) (densità superficiale).
In definitiva le ((\ref{eq6})) e ((\ref{eq7})) definiscono il moto della sonda. Ora, in generale, queste due equazioni sono disaccoppiate e vanno risolte come un sistema differenziale. Nel caso specifico si nota che dividendo la ((\ref{eq7})) per la ((\ref{eq6})) si ha:
[ \begin{equation} vdv = frac{frac{a}{\sigma}-b}{x^2} dx label{eq8} \tag{8} end{equation} ]
che è una semplice equazione differenziale a variabili separabili, che non contiene la variabile tempo. E che si integra immediatamente:
[ int_{v_0}^v v, dv = int_{x_0}^x frac{frac{a}{\sigma}-b}{x^2}, dx ]
[ v^2-v_0^2 = 2 Big( frac{a}{\sigma} - b Big) Big( frac{1}{x_0}-frac{1}{x} Big) ]
[ \begin{equation} v = \sqrt{v_0^2 + 2 Big(frac{a}{\sigma} - b Big) Big( frac{1}{x_0}-frac{1}{x} Big)} label{eq9} \tag{9} end{equation} ]
Ora vediamo che: [ \begin{equation} lim(v)_{x\rightarrow infty} = \sqrt{v_0^2+2Big(frac{a}{\sigma}-bBig)frac{1}{x_0}} equiv v_{mbox{max}} label{eq10} \tag{10} end{equation} ]
Dunque (v_{mbox{max}}) è la velocità asintotica.
Ora possiamo riprendere la ((\ref{eq6})) per determinare l'andamento del tempo in funzione dell'ascissa
[ \begin{equation} dt = frac{dx}{v(x)} = frac{dx}{\sqrt{v_0^2+2Big(frac{a}{\sigma}-bBig)Big(frac{1}{x_0}-frac{1}{x}Big)}} label{eq11} \tag{11} end{equation} ]
Posto: ( alpha = v_0^2 + 2 Big(frac{a}{\sigma}-bBig) frac{1}{x_0} ,,,,, ,,,, \beta = 2 Big(frac{a}{\sigma}-bBig) )
la ((\ref{eq11})) diventa: ( dt = \sqrt{frac{x}{alpha x - \beta}} dx ) e quindi: [ \begin{equation} t = int_0^t dt = int_{x_0}^x \sqrt{frac{x}{alpha x - \beta}}, dx label{eq12} \tag{12} end{equation} ]
L'integrale si risolve per via analitica ottenendo:
[ \begin{equation} t = frac{\beta}{2alpha^{frac{3}{2}}} ln frac{frac{alpha x_0 - \beta}{\beta}Big( \sqrt{alpha} \sqrt{frac{x}{alpha x_0-\beta}}-1 Big)^2}{frac{alpha x - \beta}{\beta}Big( \sqrt{alpha} \sqrt{frac{x}{alpha x - \beta}}-1 Big)^2} + frac{1}{alpha} Big[ (alpha x - \beta) \sqrt{frac{x}{alpha x - \beta}} - (alpha x_0 - \beta) \sqrt{frac{x}{ax_0-\beta}} Big] label{eq13} \tag{13} end{equation} ]
La ((\ref{eq13})) serve per calcolare la durata del viaggio.
Nel file EXCEL-Sonda solare sono riportati i dati completi per un calcolo di simulazione con il modello.
Si è assunto (x_0 = 5.75 ast 10^{10} m ) (pari alla distanza media Sole - Mercurio), (v_0 = 10000 frac{m}{s} ).
Risultato: (v_{mbox{max}} = 1.065 ast 10^{5} m/s ), pari a 0.035% della velocità della luce, che in pratica si raggiunge dopo circa tre anni. Per arrivare ad Alfa Centauri ci vogliono 12000 anni. Mentre il profilo di velocità è riportato sotto:
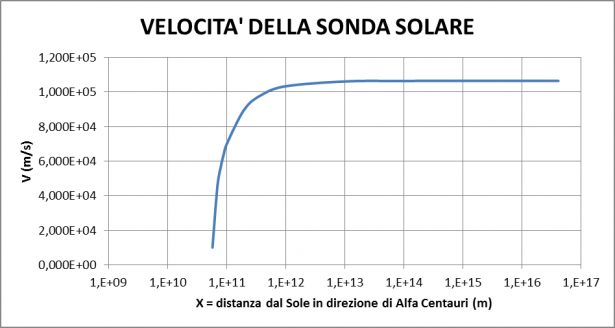
Ovviamente nessuna agenzia spaziale approverebbe una missione di tale durata.
In teoria si potrebbe pensare di raggiungere una (v_{mbox{max}}) molto superiore partendo a minore distanza
Possiamo concludere che la sonda solare è del tutto inadatta alla navigazione interstellare.
Consideriamo in alternativa l'uso della sonda solare per l'esplorazione dei pianeti e satelliti del sistema solare. Poiché Nettuno, il pianeta più lontano, dista in media dal Sole (4.5 ast 10^{12} m), una sonda solare che viaggia alla sopra riportata impiega circa 500 giorni per attraversare il sistema solare. Questo tipo di sonda, quando sarà stata sviluppata, sarà dunque un ottimo candidato a tal fine.
APPENDICE 2 - VELA LASER ↑
Lo studio della propulsione con vela laser, abbozzato negli anni '60, inizia nel 1984 con un famoso articolo di Robert Forward (R4). In anni successivi si hanno approfondimenti e revisioni, finché nel 2016 il prof. Philip Lubin scrive un ponderoso articolo, delle dimensioni di un saggio, per affrontare tutti gli aspetti importanti della propulsione laser: principi fisici, materiali della vela, tipo e natura del laser, comunicazioni, potenze ed energie richieste. Sviluppa inoltre un modello matematico completo (pagg. 64-70 di R5) al quale si rinvia il lettore interessato.L'autore di quest'articolo ha provato ad applicare il modello Lubin a un esempio pratico di dimensionamento della sonda, riportato nel file EXCEL Sonda laser, che contiene le principali equazioni e i calcoli di dettaglio.
Qui vogliamo limitarci a esporre qualche aspetto interessante del modello Lubin dal punto di vista fisico e matematico.
Notiamo che, applicando una potenza
Come si è detto sopra, la macchia del laser sulla vela ricopre, all'inizio, una piccola area della vela. Man mano che la sonda si allontana, la macchia si allarga finché, a un certo istante t0, essa ricopre esattamente l'intera vela. Per ( t le t_0 ) la spinta e l'accelerazione sono costanti e si dimostra che per
[ \begin{equation} v_0 = \sqrt{frac{P_0 (1+epsilon_r)dD}{lambda cm}} label{eq14} \tag{14} end{equation} ]
dove d= lato quadrato della batteria laser, D = lato quadrato della vela, (lambda) lunghezza d'onda del fascio laser , c = velocità della luce.
Lubin dimostra inoltre che, quando
[ L_0 = frac{dD}{2lambda} ]
dove ( lambda) è la lunghezza d'onda del raggio laser.
Inoltre
[ \begin{equation} m = m_s + m_0 label{eq15} \tag{15} end{equation} ]
Ora se assumiamo che la vela sia un parallelepipedo a base quadrata di lato D, spessore h (piccolissimo) e densità Ï, sarà:
[ \begin{equation}m_s = \rho hD^2 label{eq16} \tag{16} end{equation} ]
che si possono introdurre nella ((\ref{eq14})):
[ \begin{equation}v_0 = \sqrt{frac{P_0 (1+epsilon_r)dD}{lambda c(m_0+\rho hD^2)}} label{eq17} \tag{17} end{equation} ]
Vediamo quindi che
Intanto notiamo che la ((\ref{eq17})) può essere scritta in questo modo: ( v_o = k \sqrt{frac{D}{aD^2+b}} ) dove: (a = \rho h ) e ( b = m_0 ).
La sua derivata vale:
[ frac{dv_0}{dD} = k frac{(b-aD^2)\sqrt{frac{D}{aD^2+b}}}{2D(aD^2+b)} ]
Dove il denominatore e il termine sotto radice sono positivi. La derivata si azzera quando: [ (b-aD^2) = 0 ]
Che equivale a: [ \begin{equation}D = \sqrt{frac{b}{a}} = \sqrt{frac{m_0}{\rho h}} label{eq19} \tag{19} end{equation} ]
che può essere invertita: [ m_0 = \rho h D^2 = m_s ]
E la ((\ref{eq15})) diventa: [ m = 2m_0 ]
Si conclude che si ha un punto di stazionarietà quando la massa della vela eguaglia quella del carico utile.
Se, con un po' di pazienza, si calcola la derivata seconda, si vede che essa è negativa nel punto di stazionarietà. Dunque la
[ \begin{equation} v_{0,mbox{max}} = \sqrt{frac{P_0 (1+epsilon_r)dD}{2lambda cm_0}} label{eq20} \tag{20} end{equation} ]
Infine vogliamo far notare che quando t > t0 , e quindi ( L gt L_0 ) una parte del fascio laser fuoriesce dalla vela e pertanto una parte (crescente) della potenza fotonica viene dispersa nello spazio; la spinta e la relativa accelerazione si riducono secondo il rapporto ( Big( frac{L_0}{L} Big)^2 ), che tende a zero quando L tende all 'infinito. Lubin dimostra nell'articolo che la velocità continua a crescere fino a un limite massimo pari a: ( v_{infty} = \sqrt{2} v_0 )
Il file EXCEL Sonda Laser riporta un calcolo di simulazione - assumendo che sia:
[ v_{0,mbox{max}} = 2.8 ast 10^7 m/s ]
[ v_{infty, mbox{max}} = 4 ast 10^7 m/s, mbox{pari al 13% di c} ]
Il tempo calcolato per raggiungere Alfa Centauri è di circa 33 anni. A questo punto la sonda può trasmettere alla Terra i dati rilevati nel sorvolo, che giungeranno a terra dopo altri 4,3 anni.
Qui sotto si riporta il profilo di velocità in funzione della distanza dalla Terra.
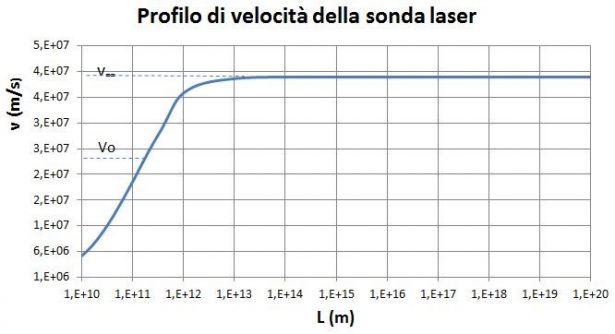
Il progetto Breakthrough Starshot, secondo quanto dichiarato da Yuri Milner, prevede di raggiungere la stessa destinazione in circa 20 anni. E' da presumere che in tal caso la sonda sia molto leggera, dell'ordine di alcuni grammi o decine di grammi. Questo richiederà spettacolari sviluppi per la miniaturizzazione dei componenti elettronici. Qualche acuto osservatore ha sostenuto che questo complicato e costosissimo progetto porterà risultati modesti, dal momento che la sonda effettuerà misure da lontano-durante il sorvolo- del sistema Alfa Centauri. Meglio sarebbe con una spesa simile e pochi rischi di insuccesso mettere in orbita terrestre un nuovo, gigantesco telescopio, dal quale ottenere risultati analoghi. Al che è stato risposto che i rischi potrebbero essere minimizzati inviando non una sonda, ma sciami di sonde (decine, centinaia): molte andrebbero perdute, altre arriverebbero a destinazione. Inoltre tutti gli studi le sperimentazioni, i prototipi della sonda con vela e del sistema laser produrrebbero un fantastico sviluppo tecnologico utile per numerose altre applicazioni.
RIFERIMENTI
- (R1) https://www.skuola.net/esercizi-svolti/problem-solving-avanzato/fionda/ (articolo effetto fionda) ↑
- (R2) travel.htmls://en.wikipedia.org/wiki/Ion_thruster (propulsione ionica) ↑
- (R3) http://www.centauri-dreams.org/?p=35862 (cronologia studi propulsione fotonica) ↑
- (R4) http://www.lunarsail.com/LightSail/rit-1.pdf (articolo Robert Forward, 1984) ↑
- (R5) https://arxiv.org/ftp/arxiv/papers/1604/1604.01356.pdf (articolo prof. Lubin) ↑
- (R6) https://www.scientificamerican.com/article/100-million-plan-will-send-probes-to-the-nearest-star1/ (progetto Breaktrough Starshot) ↑
- (R7) http://www.livescience.com/55981-futuristic-spacecraft-for-interstellar-space-travel.html (7 progetti futuristici) ↑
- (R8) https://en.wikipedia.org/wiki/Interstellar_travel (sintesi dello stato dell'arte e delle risorse/necessità tecnologiche) ↑
- (R9) https://en.wikipedia.org/wiki/Solar_sail (dati spinta fotonica vela solare) ↑
- (R10) https://www.scientificamerican.com/article/how-does-relativity-theor/ (una spiegazione del paradosso dei gemelli) ↑
- (R11) Halliday-Resnick-Walker-Fondamenti di fisica- 4° edizione- Casa Editrice Ambrosiana ↑
- (R12) Finzi- Meccanica razionale-Zanichelli ↑