L'invenzione dell'Analisi è indubbiamente riconducibile a Newton e Leibniz, mentre lo sviluppo della PDE ha richiesto ulteriori ricerche.
Gli storici del settore (R1) ritengono che il primo esempio di PDE sia dovuto a Nicolaus Bernoulli, nel 1719. Poi i matematici si sono lanciati alla ricerca di metodi analitici di risoluzione ed hanno ottenuto risultati notevoli in una serie molto importante di casi. Sono state scritte diverse e fondamentali PDE, e.g. l'equazione delle corde, della diffusione del calore in un solido, la diffusione di una specie chimica in un flusso liquido o gassoso, l'equazione di Schrödinger (che esprime la versione ondulatoria della meccanica quantistica). In campo finanziario l'equazione di Black-Scholes è stata scritta e risolta per determinare il prezzo dei derivati.Di seguito sono riportate alcune importanti PDE:
( \begin{matrix} frac{partial^2 u}{partial t^2} = v^2 frac{partial^2 u }{partial x^2}&\text{Equazione delle onde} \ frac{partial^2 f}{partial x^2} + frac{partial^2 f}{partial y^2} + frac{partial^2 f}{partial z^2} = 0&\text{Equazione di Laplace} \ rS frac{partial f}{partial S} + frac{partial f}{partial t} + frac{1}{2} \sigma^2 S^2 frac{partial^2 f}{partial s^2} -rf = 0&\text{Equazione di Black-Scholes} end{matrix})
L'ordine di una PDE è definito dall'ordine della derivata di grado maggiore. Nel caso delle PDE di 2° grado a coefficienti costanti un approccio di tipo storico, forse ormai un po' datato, individua tre tipi: ellittico, iperbolico, parabolico. In generale possiamo dire che ci sono stati solidi sviluppi teorici nella ricerca fondamentale delle condizioni di esistenza, unicità, convergenza. Quando in una PDE tali condizioni sono soddisfatte si dice che il problema è ben posto. Sono stati messi a punto metodi risolutivi di tipo analitico per numerose PDE di interesse scientifico e pratico.
Non esistono, tuttavia, metodi analitici per PDE di qualunque forma e complessità. Per questo i matematici hanno sviluppato e applicato- in gran parte nel secolo scorso- metodi approssimati di tipo numerico: elementi finiti, differenze finite, volumi finiti, … che funzionano con precisione adeguata per risolvere numerosi problemi di grande interesse pratico.
Questo ha dato luogo a grandi sviluppi applicativi. Ad es. la fluodinamica computazionale, che integra le PDE di Navier-Stokes, viene usata correntemente per progettare l'ala degli aerei, il profilo della scocca per le auto da competizione e non, la forma della carena della barche da regata (R6).
E' utile lo studio di tali metodi per chi intende dedicarsi in futuro ad attività tecnico-scientifiche.
In questo articolo proviamo a descrivere/risolvere un problema con il metodo delle differenze finite.
Valvola di alimentazione di un motore d'auto
Desideriamo studiare il comportamento di un organo mobile di un motore a combustione interna: la valvola di alimentazione. Come sappiamo il motore di un'auto produce la spinta necessaria al moto per mezzo di un processo ciclico di natura termodinamica, trasformando l'energia chimica in energia meccanica. Per far questo si alimenta ai cilindri una miscela gassosa aria-combustibile per il tramite di una valvola di alimentazione. Dopo la chiusura della valvola avviene la reazione chimica di combustione con produzione di calore, aumento della temperatura e della pressione sul pistone, azione sul medesimo e conversione del suo moto alternativo in moto rotatorio dell'albero motore. Al termine della reazione i gas esauriti sono scaricati dal cilindro tramite una valvola di scarico. L'immagine seguente riporta un motore a scoppio sezionato.
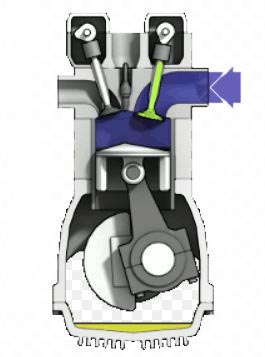
Consideriamo il condotto di alimentazione della miscela (parte ricurva colorata in blu) e la valvola di alimentazione (in verde) che regola il suo flusso. La valvola è soggetta a un moto alternativo (avanti/indietro) che provoca l'apertura/chiusura del foro di ingresso alla camera di combustione. Il moto della valvola è prodotto da un organo rotante, la camma (in alto a destra sopra la valvola), situata in un apposito carter sulla testata del motore. L'immagine sotto riporta un esempio di valvola.

La possiamo assimilare a un cilindro. Da momento che il rapporto lunghezza/diametro è > 10, è lecito immaginarla come monodimensionale.
Lo scopo del nostro esercizio è determinare l'andamento della temperatura lungo l'asse della valvola al variare del tempo, nel transitorio che si determina tra l'accensione del motore e la sua messa a regime. Conoscendo tale andamento un tecnico potrebbe fare dei calcoli di stress termomeccanico al quale è sottoposta la valvola e determinare la sua dilatazione, ai fini di una progettazione precisa degli organi meccanici coinvolti.
Come anticipato possiamo ritenere che temperatura della valvola sia variabile lungo il suo asse (x) mentre sia uniforme su ogni sezione trasversale.
Il seguente disegno schematico riproduce il funzionamento della valvola.
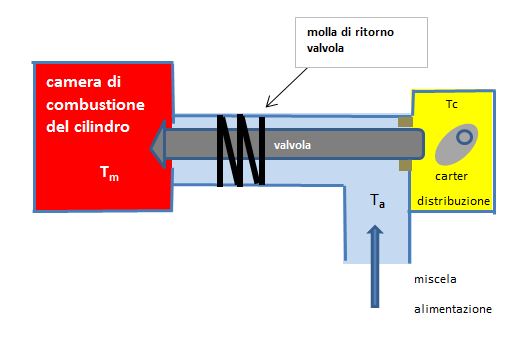
L'estremità sinistra della valvola è a contatto con la camera di combustione del cilindro, che si trova ad alta temperatura. Sappiamo che la combustione della miscela produce una temperatura anche superiore a 2500 °C, ma dopo lo scarico dei gas combusti è rinfrescata dalla miscela alimentata. Assumiamo che la temperatura media dei gas nel cilindro sia 1300°C. L'estremità destra della valvola pesca nel carter della distribuzione, che contiene olio di lubrificazione (assumiamo alla temperatura di 80°C). La camma nel carter provvede al moto alternativo della valvola con la conseguente apertura-chiusura dell'alimentazione al motore. La miscela di alimentazione (azzurra), che proviene dall'iniettore, supponiamo sia a temperatura ambiente (20°C). La valvola è lambita, nella sua superficie laterale, dalla miscela fresca in alimentazione. Supponiamo che la valvola sia costruita con una lega speciale, denominata Invar, adatta per organi meccanici di precisione. Di questa lega sono note le proprietà (R2).
Ora immaginiamo che il sig. Rossi entri in garage, accenda il motore della sua auto e parta. Desideriamo calcolare l'andamento della temperatura lungo la valvola in funzione del tempo. E intuitivo vedere che durante la marcia del motore la valvola assorbe calore dall'estremità sinistra (x=0), disperde calore lungo la superficie laterale, trasferendolo alla miscela nel condotto di alimentazione al motore. Cede o riceve calore alla sua estremità destra (x=L) dall'olio del carter.
Dobbiamo ora scrivere l'equazione PDE che esprime l'andamento della temperatura lungo l'asse x della valvola al variare del tempo. Lo sviluppo richiede una serie di ipotesi sulla natura fisica del fenomeno ed alcuni passaggi matematici che sono riportati in APPENDICE 1. Qui ci limitiamo a riportare la forma conclusiva della PDE sulla base degli scambi di calore sopra descritti:
[ \begin{equation} frac{partial T}{partial t} = D frac{partial^2 T}{partial x^2} - G(T-T_a) label{eq1} end{equation} ]
Essa può essere compresa, in sintesi, facendo riferimento a un bilancio energetico per un tronchetto cilindrico di spessore infinitesimo
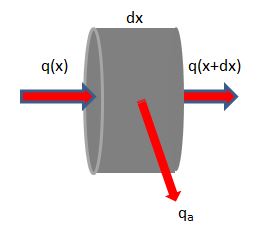
Il termine di sinistra della PDE esprime l'aumento di temperatura del tronchetto in funzione del tempo, che è proporzionale all'accumulo di energia per apporto termico. Il termine di destra è costituito da due elementi. Il primo è proporzionale al bilancio di calore (entrata - uscita) dovuto alla propagazione per conduzione nel metallo della valvola lungo l'asse x; il secondo (in diminuzione) rende conto della dispersione di calore lungo la superficie laterale del tronchetto, calore che è ceduto dalla valvola alla miscela nel condotto di alimentazione al motore.
Dove D e G sono delle costanti spiegati in APPENDICE 1, mentre
Ora vediamo come si imposta uno schema risolutivo con il metodo delle differenze finite. Si divide la lunghezza della valvola in
Ora si riscrive la nostra PDE approssimando le derivate parziali con sviluppi della Formula di Taylor opportunamente troncata:
[ \begin{equation} frac{partial T}{partial t} approx frac{T_{i,j+1}-T_{i,j}}{Delta t} label{eq2}end{equation}]
[ \begin{equation} frac{partial^2 T}{partial x^2} approx frac{T_{i+1,j}-2T_{i,j}+T_{i-1,j}}{Delta x^2} label{eq3} end{equation}]
dove: (Delta x = frac{L}{N_x} )
essendo
Le ((\ref{eq2})) e ((\ref{eq3})) introdotte nella ((\ref{eq1})), diventano:
[ \begin{equation} frac{T_{i,j+1}-T_{i,j}}{Delta t} = frac{D}{Delta x^2} (T_{i+1,j}-2T_{i,j}+T_{i-1,j})-G(T_{i,j+1}-T_a) label{eq4} end{equation}]
Poniamo
[ \begin{matrix} frac{DDelta t}{Delta x^2} = A&& GDelta t = Bend{matrix}]
(osserviamo che A e B sono due parametri adimensionali)
La ((\ref{eq4})) si risolve rispetto a (T_{i,j+1}), ottenendo:
[ \begin{equation} T_{i,j+1} = frac{A(T_{i+1,j}+T_{i-1,j})+(1-2A)T_{i,j}+BT_a}{1+B} label{eq5} end{equation} ]
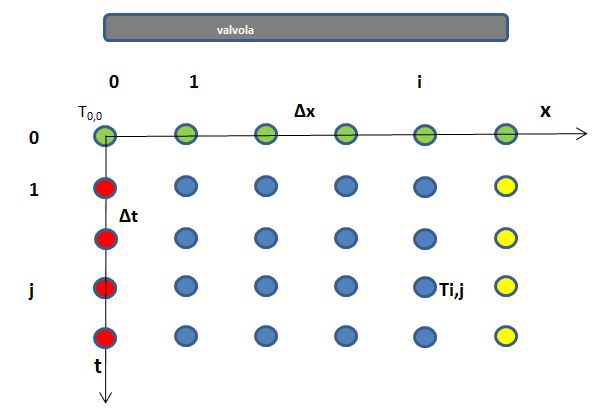
Lo schema risolutivo ((\ref{eq5})) è di tipo esplicito (R3, R4) e permette di determinare la temperatura nel reticolo. Il disegno sotto riportato, denominato stencil, evidenzia le celle che intervengono nel calcolo della ((\ref{eq5})):
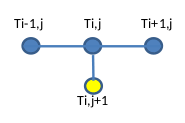
Il calcolo della temperatura per la cella gialla richiede la conoscenza delle temperature delle celle blu, che si riferiscono all'intervallo temporale precedente. Questo semplice algoritmo permette di determinare in modo ricorrente tutti i valori di temperatura passo- passo spostandoci da sinistra verso destra e passando poi alla riga temporale successiva. A patto di aver assegnato le condizioni iniziali, che nel reticolo prima visto sono le temperature della prima riga (in verde) per t=0 e le condizioni al contorno agli estremi della valvola. Solitamente si assegnano al contorno le temperature della prima colonna (in rosso) e dell'ultima colonna (in giallo) del reticolo.
Nel nostro caso, allo scopo di rendere problema più realistico, si è deciso invece di assegnare a entrambe le estremità della valvola l'equazione che definisce il flusso di calore per lo scambio termico convettivo: a sinistra tra la sezione della valvola e i gas del cilindro, a destra tra la sezione della valvola e l'olio lubrificante del carter. La trattazione fisico-matematica per queste particolari condizioni al contorno è riportata nell'APPENDICE 2.
In sintesi, risolvendo le equazioni di APPENDICE 2 si determinano i valori della prima ed ultima colonna del reticolo mentre con la formula (5) si risolve a cascata i profilo di temperatura lungo la valvola da sinistra a destra.
Il metodo esplicito di equazione ((\ref{eq5})) è molto comodo e di facile uso, ma presenta un inconveniente: è condizionatamente convergente. Questo vuol dire che si deve soddisfare una condizione per la convergenza, nel nostro caso la seguente (R3):
[ \begin{equation}A = frac{DDelta t}{Delta x^2} le frac{1}{2} label{eq6} end{equation} ]
L'uso di EXCEL rende facile costruire il reticolo risolutivo dell'equazione ((\ref{eq5})). Ogni punto del reticolo è associato ad una cella EXCEL. Il file EXCEL allegato a questo articolo riporta una simulazione completa, evidenziata dal diagramma seguente.
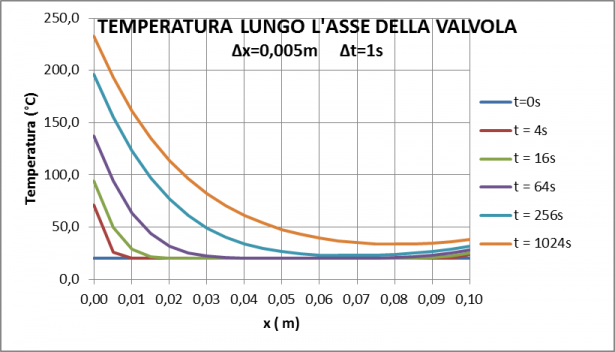
Quando di affrontano calcoli di tipo numerico, che intendono approssimare la eventuale o ipotetica soluzione analitica, esiste il problema di raggiungere la convergenza. Il metodo pratico che si adotta è quello di fare calcoli di simulazioni a passi (in questo caso (Delta x) e (Delta t)) sempre più piccoli. Si ritiene raggiunta la convergenza quando un'ulteriore riduzione dei passi modifica i risultati in misura trascurabile (ad es. inferiore all'1%).
Esiste, tuttavia, un problema di dimensioni del file di elaborazione. Maneggiare uno SHEET molto più grande di quello usato comincia a diventare un po' scomodo. Ottenere risultati precisi, i.e. ottenere la convergenza, è possibile, con facilità, costruendo un semplice codice con il modello proposto. E' quanto si è fatto e il diagramma successivo riporta l'andamento della temperatura. Per far questo la lunghezza della valvola (10 cm) è stata suddivisa in 75 zone, mentre l'intervallo temporale di 1024 s è stato suddiviso in 10240 passi. Quindi il reticolo di calcolo è di 768 mila celle.
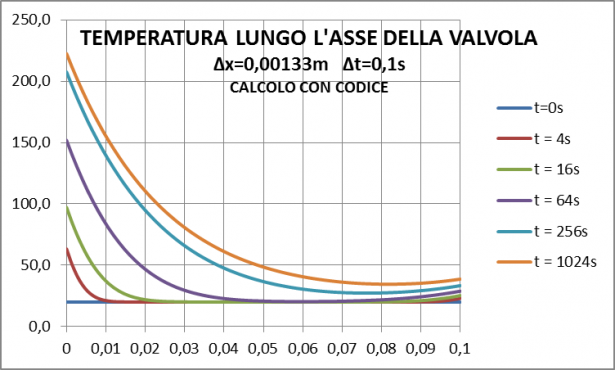
Osserviamo che la curva arancione, corrispondente a t=1024 s, pari a circa 17 minuti, non si modifica se si proseguono i calcoli per tempi più lunghi. Questo vuol dire che tale profilo rappresenta la situazione di motore a regime. Su tale curva le temperature agli estremi sono, rispettivamente 222°C e 39°C. Notiamo che all'estremità sinistra la differenza di temperatura tra i gas di combustione e la valvola è pari a 1300-222 = 1078°C (Questo, a prima vista potrebbe apparire strano a qualcuno. Ma a ben vedere è più che normale. Se mettiamo una pentola a bollire su un fornello domestico la temperatura della fiamma del metano è dell'ordine dei 1000 °C, mentre la pentola ha una temperatura di gran lunga inferiore, diciamo 150-200 °C). Questo è quanto ci dicono i calcoli sulla base delle ipotesi di questo modello fenomenologico.
CONCLUSIONE
L'articolo ha definito un problema di interesse pratico in forma di PDE e lo ha risolto con un noto metodo esplicito, che risulta particolarmente semplice da spiegare e applicare. Che tuttavia presenta l'inconveniente di una convergenza condizionata. Sono stati sviluppati in seguito altri algoritmi di discretizzazione, ad es. quello di Crank-Nicholson, che sono molto più complessi e producono sistemi di equazioni lineari di grandi dimensioni, per i quali esistono comunque efficienti metodi risolutivi. Tali algoritmi sono spesso incondizionatamente convergenti. Gli articoli nei RIFERIMENTI contengono informazioni sull'argomento.
APPENDICE 1 - EQUAZIONE DEL CALORE
L'equazione del calore ( di Fourier) esprime il meccanismo di conduzione in un corpo solido omogeneo e isotropo. Nella sua forma generale, riferita a un elemento infinitesimo di volume[ frac{partial T}{partial t} = D Big( frac{partial^2 T}{partial x^2} + frac{partial^2 T}{partial y^2} +frac{partial^2 T}{partial z^2} Big) ]
Mentre nel caso unidimensionale diventa:
[ frac{partial T}{partial t} = DBig(frac{partial^2 T}{partial x^2}Big)]
Nel nostro esempio la situazione è leggermente più complicata, poiché immaginiamo uno scambio termico con la miscela attraverso la superficie laterale e scambi termici a sinistra con i gas di combustione, a destra con l'olio del carter.
Proviamo dunque a sviluppare l'equazione completa per lo scambio termico. Consideriamo un pezzetto della valvola a forma di tronco conico di lunghezza infinitesima
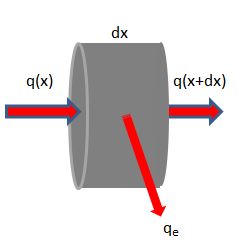
Esso riceve calore per conduzione sul lato sinistro, per mezzo di un flusso termico q(x). L'equazione elementare di conduzione del calore è data dalla formula empirica di Fourier:
[ \begin{equation} q= -k frac{partial T}{partial x} label{eq7}end{equation}]
Che esprime una semplice correlazione: Il flusso termico (dimensioni W/m^2) è proporzionale al gradiente di temperatura secondo una costante
Dunque avremo un flusso di conduzione entrante, a sinistra:
[ q(x) = -k frac{partial T}{partial x} ]
Ed esiste un flusso di conduzione uscente, a destra:
[ q(x+dx) = q(x) +frac{dq}{dx}dx]
Derivando la ((\ref{eq7})) si ottiene:
[ frac{dq}{dx} = -k frac{partial^2 T}{partial x^2} ]
Quindi: ( q(x+dx) = -kfrac{partial T}{partial x} -k frac{partial^2 T}{partial x^2} dx)
Il bilancio del flusso termico tra le due superfici (entrata - uscita) vale quindi:
[ dq = q(x+dx) - q(x) = k frac{partial^2 T}{partial x^2}dx ]
La potenza (dimensione W) relativa a tale flusso termico è data dal prodotto del flusso per la superficie e dunque vale: ( kA frac{partial^2T}{partial x^2}dx ) (dove: ( A = pi frac{d^2}{4}) è l'area della sezione del tronchetto).
Dalla superficie laterale del tronchetto esce un flusso termico di convezione ( q_a = gamma(T-T_a) ) e la corrispondente potenza vale: (gamma(T-T_a)Pdx) (dove: (P = pi d) è il perimetro della sezione del tronchetto,
Il flusso convettivo rappresenta lo scambio termico tra la parete laterale della valvola e il fluido circostante (miscela di alimentazione).
La somma algebrica delle potenze serve a far variare l'entalpia del tronchetto: ( frac{partial H}{partial t} = \rho c dV frac{partial T}{partial t} )
(dove Ï = densità, c = calore specifico a pressione costante,
In definitiva il bilancio energetico è:
[ \rho c dV frac{partial T}{partial t} = kA frac{partial^2 T}{partial x^2} dx - gamma(T-T_c)P dx ]
Che, diviso per (\rho c dV ) diventa:
[ \begin{equation} frac{partial T}{partial t} = D frac{partial^2 T}{partial x^2} -G (T-T_c) label{eq8} end{equation} ]
Dove: ( D = frac{K}{\rho c} ) è la diffusività termica, mentre: (G=frac{4gamma}{d\rho c}) è la convettività laterale.
La ((\ref{eq8})) è l'equazione che sarà usata nel modello.
APPENDICE 2 - CONDIZIONI INIZIALI E AL CONTORNO SUI FLUSSI TERMICI CONVETTIVI
Le condizioni iniziali definiscono il profilo di temperatura della valvola all'istante t=0. Nell'avviamento del motore a freddo assumiamo un profilo uniforme:[\begin{equation}\begin{matrix} T_{i,0} = T_0 = 20°C&mbox{per}&i=0,N_x label{eq9} end{matrix}end{equation}]
Veniamo ora alle condizioni al contorno.
All'estremità sinistra la valvola è in contatto con i gas di combustione (a temperatura
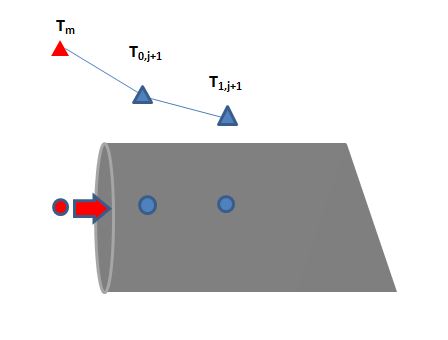
L'equazione che definisce la condizione al contorno nel punto 0 del reticolo è la seguente
[ gamma_m (T_m -T) = -k frac{partial T}{partial x} ]
Dove il termine a sinistra esprime il flusso di calore di tipo convettivo tra i gas del cilindro e la sezione della valvola all'estremità sinistra, mentre il termine a destra esprime il medesimo flusso che passa per conduzione nel metallo della valvola. Il parametro (gamma_m) è il coefficiente di scambio termico convettivo. In termini discretizzati l'equazione diventa:
[ \begin{equation}gamma_m (T_m - T_{0,j+1}) = -frac{k}{Delta x}(T_{1,j+1}-T_{0,j+1}) label{eq10}end{equation} ]
Mentre la PDE, scritta per il punto (1, j+1) del reticolo è ancora la ((\ref{eq5})):
[ \begin{equation} T_{1,j+1} = frac{A(T_{2,j}+T_{0,j})+(1-2A)T_{1,j}+BT_a}{1+B}label{eq11}end{equation} ]
Le equazioni ((\ref{eq10})) e ((\ref{eq11})) costituiscono un sistema lineare nelle due variabili. Dalla ((\ref{eq10})) si ricava:
[ \begin{equation} T_{1,j+1} = (1+\theta_m) T_{0,j+1} -\theta_m T_m label{eq12}end{equation}]
Dove (\theta_m = frac{gamma_m Delta x}{k} ) è un parametro adimensionale.
La ((\ref{eq8})) si sostituisce nella ((\ref{eq11})) che ora può essere risolta per determinar (T_{0,j+1}) e e si ha:
[ \begin{equation} T_{0,j+1} = frac{(1+B)\theta_mT_m+A(T_{2,j}+T_{0,j})+(1-2A)T_{1,j}+BT_a}{(1+B)(1+\theta_m)} label{eq13}end{equation}]
All'estremità destra la valvola è in contatto con l'olio del carter (a temperatura
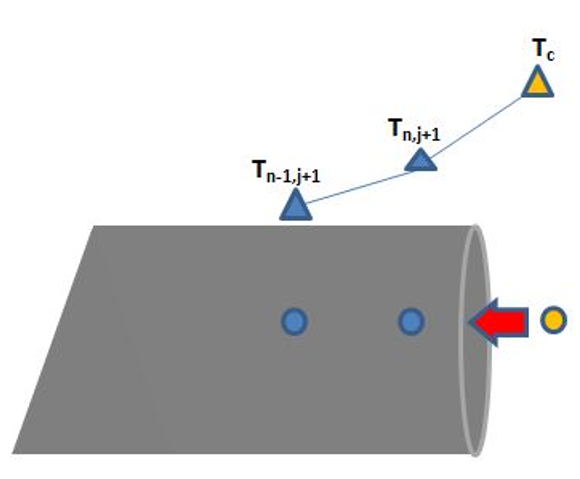
L'equazione che definisce la condizione al contorno nel punto n del reticolo è la seguente:
[ -kfrac{partial T}{partial x} = gamma_c (T_c - T) ]
In termini discretizzati essa diventa:
[ \begin{equation}-frac{k}{Delta x} (T_{n-1,j+1}-T_{n,j+1}) = gamma_c (T_c-T_{n,j+1}) label{eq14}end{equation} ]
Dve (gamma_c) è il coefficiente di scambio termico convettivo tra l'olio e la sezione finale destra della valvola.
Anche qui definiamo un parametro adimensionale ( \theta_c = frac{gamma_c Delta x}{k} ).
E risolvendo la ((\ref{eq10})) si ha:
[ \begin{equation} T_{n,j+1} = frac{T_{n-1,j+1}+\theta_c T_c}{1+\theta_c} label{eq15}end{equation} ]
In questo modo, con le ((\ref{eq13})) e ((\ref{eq15})) sono state determinate le temperature alle due estremità della valvola.
In definitiva l'algoritmo costituito dalle ((\ref{eq5})), ((\ref{eq9})), ((\ref{eq13})), ((\ref{eq15})) permette di calcolare passo-passo il profilo di temperatura lungo il reticolo che discretizza la valvola.
RIFERIMENTI
- (R1) http://www.math.harvard.edu/archive/21a_fall_14/exhibits/cajori/cajori.pdf (sviluppo storico PDE) ↑
- (R2) http://www.nickel-alloys.net/invar_nickel_iron_alloy.html#_Other_Applications (proprietà Invar) ↑
- (R3) http://www.dmmm.uniroma1.it/~francesca.pitolli/Didattica/dispPDE.pdf
(teoria metodi numerici per equazioni alle derivate parziali) ↑ - (R4) http://tiziano19661.interfree.it/pdf1011/Paraboliche.pdf (soluzione numerica equazione del calore) ↑
- (R5) https://en.wikipedia.org/wiki/Heat_equation#Statement_of_the_equation (equazione diffusione del calore) ↑
- (R6) Ian Stewart-Le 17 equazioni che hanno cambiato il mondo-Einaudi ↑
Le immagini del motore e della valvola sono tratte da Wikipedia, con elaborazioni.


