Anteprima
Vedrai una selezione di 8 pagine su 34
Soluzione PDE con metodo Crank-Nicolson Pag. 1 Soluzione PDE con metodo Crank-Nicolson Pag. 2
Anteprima di 8 pagg. su 34.
Scarica il documento per vederlo tutto.
Scarica
Soluzione PDE con metodo Crank-Nicolson Pag. 6
Anteprima di 8 pagg. su 34.
Scarica il documento per vederlo tutto.
Scarica
Soluzione PDE con metodo Crank-Nicolson Pag. 11
Anteprima di 8 pagg. su 34.
Scarica il documento per vederlo tutto.
Scarica
Soluzione PDE con metodo Crank-Nicolson Pag. 16
Anteprima di 8 pagg. su 34.
Scarica il documento per vederlo tutto.
Scarica
Soluzione PDE con metodo Crank-Nicolson Pag. 21
Anteprima di 8 pagg. su 34.
Scarica il documento per vederlo tutto.
Scarica
Soluzione PDE con metodo Crank-Nicolson Pag. 26
Anteprima di 8 pagg. su 34.
Scarica il documento per vederlo tutto.
Scarica
Soluzione PDE con metodo Crank-Nicolson Pag. 31
1 su 34
Disdici quando vuoi 162x117
Disdici quando
vuoi
Acquista con carta
o PayPal
Scarica i documenti
tutte le volte che vuoi
Sintesi
L'argomento equazioni alle derivate parziali è stato trattato su Skuola.net (R1). Ad esso si rimanda per una introduzione sulla PDE (Partial Derivative Equation) e per la descrizione/soluzione di un esempio applicativo di interesse tecnico: lo studio del transitorio termico per la valvola di alimentazione di un motore a scoppio. Questo articolo si propone di riesaminare e risolvere lo stesso problema con un metodo numerico diverso e più efficiente.

Qui sotto è riportato il disegno del motore con la valvola di alimentazione (in verde).

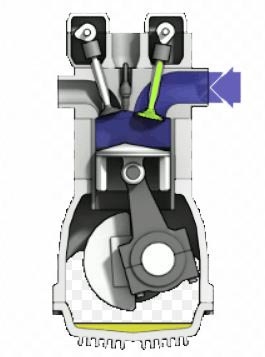
Sezione motore a scoppio con valvola di alimentazione

Mentre la valvola è disegnata sotto:

Valvola motore

La valvola di alimentazione riceve alla sua estremità sinistra (sx) un flusso termico dalla camera di combustione, che si è supposto abbia una temperatura media
[math] T_m = 1300 °C [/math]
, viene lambita dal flusso di miscela in alimentazione (freccia in blu nel disegno del motore), che ha temperatura
[math] T_a = 20 °C [/math]
, la quale asporta calore lungo tutta la superficie laterale della valvola. Infine l'estremità destra (dx) della valvola è a contatto con la camma che pesca nell'olio del carter (che assumiamo avere temperatura costante pari a
[math] T_c = 80 °C [/math]
) e quindi avviene uno scambio termico (in entrata o uscita) tra la valvola e l'olio.

La valvola ha la forma di un cilindro sottile e viene schematizzata come un'asta, vale a dire un corpo monodimensionale.

L'equazione che descrive il fenomeno in forma indefinita:



[math] \begin{equation} \frac{\partial T}{\partial t}=D \frac{\partial^2 T}{\partial x^2}-G(T-T_a) \tag{1} \end{equation} [/math]




è di tipo lineare parabolico e correla l'andamento della temperatura (T) lungo l'asse della valvola in funzione del tempo (t). Il termine
[math] G(T-Ta) [/math]
nel membro a destra rappresenta la perdita di calore della valvola mentre viene lambita dal flusso della miscela di alimentazione al motore. La derivazione della (eqref{eq1}) è descritta in dettaglio nell'articolo citato.

Risolvere l'equazione vuol dire determinare (nel nostro caso per via numerica) la funzione T (x, t) sulla base della condizione iniziale (t=0) ed al contorno alle estremità (x=0 e x= L).

Nel precedente articolo questo esempio è stato risolto approssimando le derivate parziali con uno schema molto semplice di differenze finite che si presta ad una soluzione diretta, con il metodo di Eulero esplicito. In pratica si è costruito un reticolo spazio-temporale

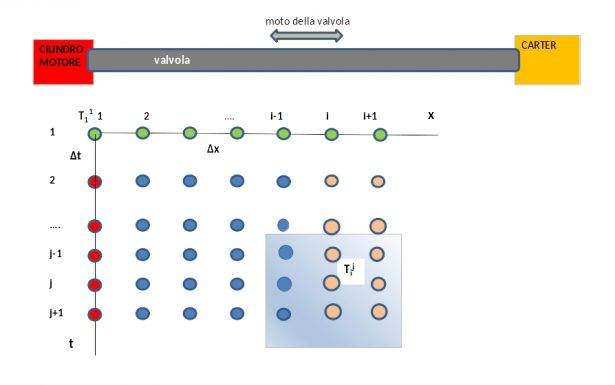
Schema differenze finite - Metodo di Eulero esplicito

dove lo spazio è riportato in ascissa ed il tempo in ordinata. Con il metodo esplicito di Eulero si risolve ogni cella del reticolo spostandosi da sinistra a destra fino a completare le riga per passare poi alla riga temporale successiva. Il metodo, descritto in dettaglio nell'articolo citato, è molto semplice e si presta a essere facilmente usato con EXCEL, ma ha un serio problema di convergenza. Questo richiede di usare un passo temporale molto piccolo. In tal modo per ottenere la convergenza, ed anche un ragionevole precisione, è necessario costruire un reticolo di grandi dimensioni. Ciò che comporta un notevole consumo di memoria del computer ed un tempo di elaborazione abbastanza lungo.


METODO DI CRANK-NICOLSON


Per rimediare alle difficoltà di convergenza gli esperti hanno sviluppato nuovi schemi alle differenze finite per approssimare le derivate parziali evitando i problemi del metodo di Eulero. In letteratura (R2) si trovano diversi metodi, uno dei più usati è quello di due matematici statunitensi John Crank e Phyllis Nicolson (in seguito C-N) che vogliamo applicare in questo articolo. Vediamo come è fatto e come si usa.

Con il metodo C-N le derivate sono approssimate come segue:


[math] \begin{equation} \frac{\partial T}{\partial t} \approx \frac{T^{j+1}_i - T^j_i}{\Delta t} \tag{2} \end{equation} [/math]



[math] \begin{equation} \frac{\partial^2 T}{\partial x^2} \approx \frac{1}{2(\Delta x)^2} \Big( T^{j+1}_{i-1} -2 T^{j+1}_{i} + T^{j+1}_{i+1} + T^{j}_{i-1} -2 T^j_i + T^j_{i+1}\Big) \tag{3} \end{equation} [/math]




(dove: pedice = spazio, apice = tempo)

Notiamo che la derivata temporale è molto semplice (come nel metodo di Eulero esplicito) mentre la derivata spaziale è di tipo più complesso, in quanto coinvolge sei elementi del reticolo spazio-temporale, suddivisi in due gruppi di tre elementi per ogni valore temporale, che è rappresentato dal seguente schema (stencil):

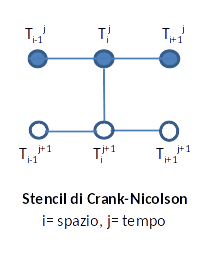
Stencil di Crank-Nicolson

L'approssimazione
[math](2)[/math]
è dunque un po' complicata ma comporta un errore di troncamento quadratico nello spazio e nel tempo quindi una maggior precisione rispetto allo schema di Eulero esplicito. Il metodo è convergente ed incondizionatamente stabile. Ha lo svantaggio di essere implicito, il che vuol dire che la soluzione dello stencil richiede la soluzione di un sistema di equazioni lineari, come vedremo.

Per completare lo schema risolutivo è necessario approssimare alle differenze finite anche il secondo termine al secondo membro della
[math](1)[/math]
:



[math] \begin{equation} G(T-T_a) \simeq G(T^{j+1}_i - T_a) \tag{4} \end{equation} [/math]




Infine dobbiamo fornire la condizione iniziale:



[math] t = 0 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, T (x, t= 0) = T_0 [/math]




Vale a dire:



[math] \begin{equation}T^1_i = T_0, \, \, \, \, \, \, \, \, \mbox{ per } i=1, n \tag{5} \end{equation} [/math]




E le condizioni al contorno, che nel nostro caso, come nell'articolo precedente, sono del tipo di Neumann (R4), vale a dire sono espresse da derivate:


Estremità sx ( lato motore) :
[math] \gamma_m (T_m - T) = -k \frac{\partial T}{\partial x} [/math]



Estremità dx (lato carter):
[math] \gamma_c (T_c - T) = k \frac{\partial T}{\partial x} [/math]



Nota: sx e dx significano rispettivamente sinistra e destra.

(dove
[math] k [/math]
è la conduttività termica della valvola, mentre
[math] \gamma_m [/math]
e
[math] \gamma_c [/math]
e sono i coefficienti di scambio termico convettivo lato motore e lato carter)

Entrambe le condizioni al contorno traducono il principio fisico per cui il flusso termico convettivo, tra l'estremità della valvola ed il fluido che la lambisce, eguaglia il flusso termico conduttivo nel metallo alle estremità della valvola: in definitiva il principio di conservazione dell'energia.

Anche per le condizioni al contorno le derivate sono approssimate dalle loro differenze finite:



[math] \begin{equation} \gamma_m (T_m - T_{1,j+1}) = \frac{k}{\Delta x} (T^{j+1}_1 - T^{j+1}_2) \tag{6} \end{equation} [/math]



[math] \begin{equation} \gamma_c (T_c - T_{n,j+1}) = \frac{k}{\Delta x}(T^{j+1}_{n-1}-T^{j+1}_n) \tag{7} \end{equation} [/math]




Inoltre è conveniente concentrare i parametri creandone cinque nuovi, in questo modo:


[math] \mu = G\Delta t [/math]



[math] \Theta_c = \gamma_c \frac{\Delta x}{k} [/math]



[math] \Theta_m = \gamma_m \frac{\Delta x}{k} [/math]



[math] \lambda = \frac{D}{2} \frac{\Delta t}{(\Delta x)^2} [/math]



[math] \alpha = 1 + 2\lambda + \mu [/math]




Non è irrilevante notare che tali parametri sono tutti adimensionali.

Ora le
[math](2)[/math]
e
[math](3)[/math]
possono essere sostituite nella
[math](1)[/math]
facendo uso dei parametri concentrati:



[math] \begin{equation} -\lambda T^{j+1}_{i-1} + \alpha T^{j+1}_{i} - \lambda T^{j+1}_{i+1} = \lambda T^{j}_{i-1} + (1 -2\lambda) T^{j}_{i} + \lambda T^{j}_{i+1} + \mu T_a \tag{8} \end{equation} [/math]




Osserviamo che la
[math](8)[/math]
è stata scritta portando a sx le temperature relative allo step temporale
[math] j+1 [/math]
, a dx quelle per lo step
[math] j [/math]
.

Analogamente si possono riscrivere e semplificare le
[math](6)[/math]
e
[math](7)[/math]
in forma sintetica:



[math] \begin{equation} (1 + \Theta_m ) T^{j+1}_1 - T^{j+1}_2 = \Theta_m T_m \tag{9} \end{equation} [/math]



[math] \begin{equation} -T^{j+1}_{n-1} + (1+\Theta_c) T^{j+1}_n = \Theta_c T_c \tag{10} \end{equation} [/math]




In definitiva le equazioni
[math](8)[/math]
,
[math](9)[/math]
,
[math](10)[/math]
con la condizione iniziale
[math](5)[/math]
risolvono il nostro problema. Vediamo come.

Notiamo che la
[math](8)[/math]
è in realtà un sistema di
[math] n - 2 [/math]
equazioni lineari (con
[math]i = 2, n -1[/math]
), mentre le
[math](9)[/math]
e
[math](10)[/math]
sono equazioni singole. Quindi il sistema
[math](8)[/math]
,
[math](9)[/math]
,
[math](10)[/math]
è costituito da equazioni in altrettante variabili
[math] T^{j+1}_i [/math]
dove
[math] i=1, n[/math]
per ogni valore
[math]j+1[/math]
. In altri termini abbiamo creato un sistema lineare a matrice quadrata
[math] n \times n [/math]
. Se risolviamo il sistema a partire dalla condizione iniziale
[math](5)[/math]
la prima riga temporale è nota: tutti i termini valgono
[math]T_0[/math]
. Vediamo quindi che i membri di
[math]dx[/math]
del sistema di equazioni sono noti e costituiscono il termine noto del sistema di equazioni. Non c'è che da risolvere il sistema lineare
[math] n \times n [/math]
per calcolare il profilo di temperatura della valvola lungo l'asse x per la riga temporale
[math]j+1[/math]
.

Tuttavia a questo punto vien da pensare che la faccenda diventi complessa. Infatti è il numero di punti nel reticolo spaziale, che si ottiene dividendo la lunghezza della valvola in
[math]n-1[/math]
intervalli uguali di lunghezza
[math] \Delta x [/math]
. Ora per avere una ragionevole precisione di calcolo è facile immaginare che l'intervallo
[math] \Delta x [/math]
debba essere abbastanza piccolo. In tal modo è facile rendersi conto che la
[math](8)[/math]
sarà costituita da decine e forse centinaia di equazioni lineari. Ma non c'è motivo di preoccuparsi. Esistono algoritmi di soluzione semplici e molto precisi per la soluzione iterativa di tali sistemi( Jacobi e meglio ancora Gauss-Seidel). Nel nostro caso, poi, la situazione è ancora più semplice perché la matrice della
[math](8)[/math]
è tridiagonale ed esiste un metodo diretto (vale a dire non iterativo) per la soluzione esatta. Vediamo di visualizzare come mai il sistema risolutivo è tridiagonale. Intanto notiamo che ogni equazione del gruppo
[math](8)[/math]
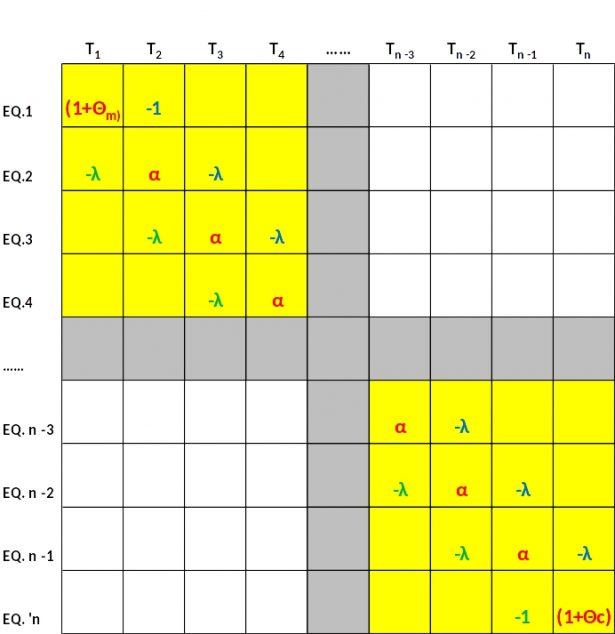
contiene solo tre variabili, quella sulla diagonale centrale e quelle a lati sx e dx. Di seguito vediamo come è fatta la matrice dei coefficienti del sistema:

Matrice dei coefficienti del sistema

(Le temperature riportate in testa al disegno sono prive dell'apice temporale j+1, che viene sottinteso).

Notiamo che sulla diagonale principale abbiamo tutti coefficienti uguali, pari a α, tranne il primo e l'ultimo, che sono rispettivamente i coefficienti delle equazioni al contorno
[math](8)[/math]
e (
[math](9)[/math]
. Le diagonali immediatamente a dx ed a sx sono piene di valori uguali, pari a -», tranne gli estremi.

In conclusione la matrice dei coefficienti del sistema è tridiagonale ed i valori delle componenti matriciali sono delle costanti, che rimangono invariate passando da una riga temporale all'altra.

La matrice dei termini noti ovviamente deve essere variabile per ogni riga temporale. È un vettore colonna il cui elemento tipico è dato in forma generale da:



[math] \lambda T^j_{i-1} + (1-2\lambda) T^j_i + \lambda T^j_{i+1} + mu T_a, \, \, \, \, \, \, \, \, i = 2, n-1 [/math]




Mentre i componenti
[math]1[/math]
ed
[math]n[/math]
sono rispettivamente:



[math] \Theta_m T_m \, \, \, \, \, \, \, \, \mbox{ e } \, \, \, \, \, \, \, \, \Theta_c T_c [/math]




In breve il meccanismo di calcolo è facilmente intuibile: si parte dalla prima riga temporale, dove



[math] T^1_i = T_0 \, \, \, \, \, \, \, \, \mbox{ per } i = 1, n [/math]




Ora si calcolano le componenti del vettore dei termini noti usando le
[math] T^{1}_i [/math]
. A questo punto si risolve il sistema
[math] n \times n [/math]
ottenendo le temperature per la seconda riga temporale
[math]j = 2[/math]
. Si ripete il procedimento per tutte le righe temporali successive. Notiamo che mentre il reticolo spaziale è definito dalla lunghezza della valvola, il reticolo temporale è teoricamente illimitato. Tuttavia è evidente che dopo un tempo abbastanza lungo si raggiunge una situazione di equilibrio termico: il profilo di temperatura lungo l'asse x non cambia, quindi la valvola ha raggiunto lo stato stazionario e non c'è motivo di aggiungere altre righe.

Ci manca di precisare come si risolve il sistema tridiagonale: ci ha pensato il fisico e matematico Llewelynn Thomas che ha costruito un semplice algoritmo (R5). Perché esso funzioni è necessario che la diagonale della matrice dei coefficienti sia strettamente dominante per righe, ciò che si verifica nel nostro problema.

Le equazioni del modello sono state incorporate in un semplice codice VBA che contiene la routine dell'algoritmo di Thomas. Il codice è stato usato per simulare il comportamento della valvola a partire dalla condizione iniziale per diverse dimensioni del reticolo. Converge sempre perfettamente.

La simulazione più precisa ottenuta con il modello ha richiesto un reticolo
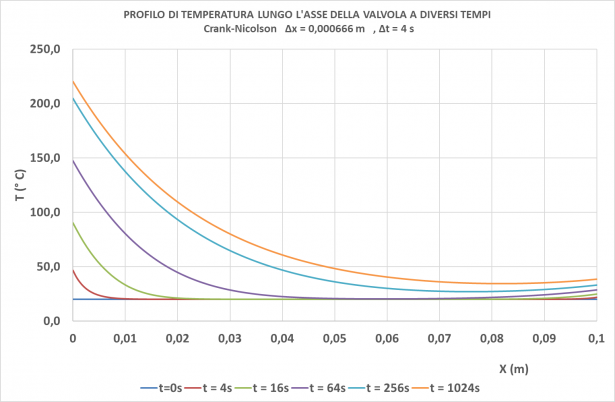
[math] i \times j = 150 \times 256 =38400 [/math]
celle ed il profilo di temperatura a tempi crescenti è riportato sotto



Riproponiamo sotto il diagramma da articolo precedente (R1), risolto con metodo di Eulero esplicito:



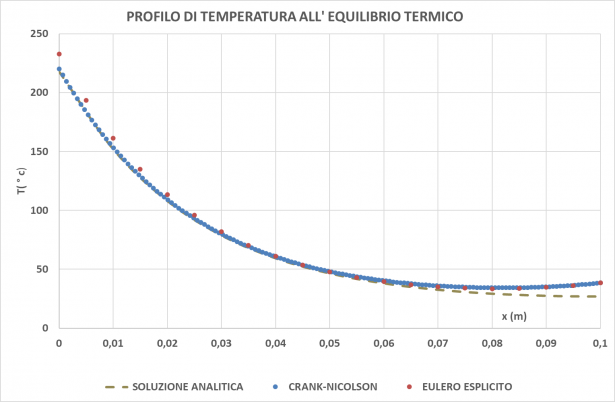
Si nota che i profili di Eulero e C-N sono abbastanza vicini, tuttavia all'estremità sx C-N è molto più preciso di Eulero, mentre all'estremità dx i due metodi sono quasi coincidenti e sovrastimano di circa 9 °C la soluzione esatta. Complessivamente C-N è più preciso di Eulero, ha richiesto un reticolo enormemente più piccolo (38 mila contro 768 mila punti) e tempo di elaborazione molto inferiore. Si può concludere che è sicuramente preferibile.

Il codice VBA e tutti i dati, parametri, calcoli, diagrammi, sono riportati nel file EXCEL associato all'articolo.


APPENDICE-SOLUZIONE ANALITICA ALL'EQUILIBRIO TERMICO


All'equilibrio termico, che in teoria si raggiungerebbe dopo un tempo infinito, l'equazione
[math](1)[/math]
si semplifica dal momento la derivata temporale è nulla:
[math] \frac{\partial T}{\partial t} = 0 [/math]
.

Questo vuol dire che scompare la variabile tempo. Il modello si semplifica e la derivata spaziale non è più parziale:



[math] \begin{equation} \frac{d^2 T}{dx^2} = \frac{G}{D} (T-T_a) \tag{11} \end{equation} [/math]



Che è del tipo:
[math] \frac{d^2 T}{dx^2} = a^2 (T-b) [/math]
dove
[math] a^2= \frac{G}{D}, b = T_a [/math]
.

È questa una equazione differenziale lineare del secondo ordine la cui soluzione è:



[math] \begin{equation} T=k_1 \exp(ax)+k_2 \exp(-ax)+b \tag{12} \end{equation} [/math]




Si impongono ora le condizioni al contorno di Neumann:


Estremità sx, x=0:
[math] {\frac{dT}{dx}}_{x=0} = -\frac{\gamma_m}{k}(T_m-T(0)) [/math]



Estremità dx, X =L:
[math] {\frac{dT}{dx}}_{x=L} = -\frac{\gamma_c}{k}(T_c-T(L)) [/math]




In questo modo si ottiene un sistema lineare (2 \times 2) nelle variabili
[math]k_1[/math]
e
[math]k_2[/math]
che si risolve ad es. con la regola di Kramer. La soluzione esatta nel caso della nostra valvola determina le seguenti temperature alle estremità:
[math] T(0) = 218°C, T(L) = 27°C [/math]
.

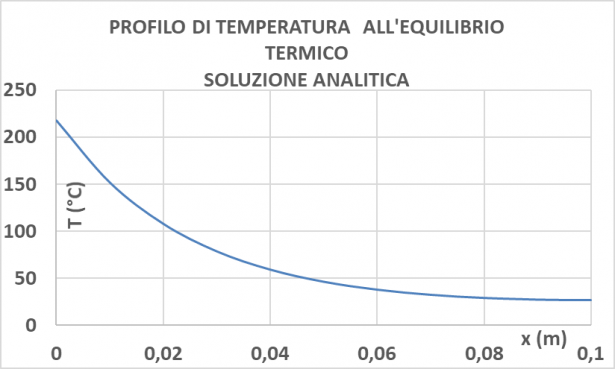
Profilo di temperatura all'equilibrio termico - Soluzione analitica

Il profilo di temperatura, riportato nel diagramma sopra, sembra di tendenza asintotica, ma si tratta di un inganno visivo. Nella realtà esiste un minimo relativo, situato a circa 0,1 mm dall'estremità dx della valvola. Il significato fisico del fenomeno è semplice da capire: il flusso in controcorrrente della miscela in alimentazione raffredda la valvola a temperature inferiori a 30°C. Tuttavia la valvola all'estremità dx è in contatto con l'olio caldo del carter (
[math]T_c = 80° C[/math]
) che provoca un leggero aumento di temperatura in tale zona.


RIFERIMENTI


Estratto del documento

525 312,3 129,4 62,7 43,5 51,4

530 312,4 129,5 62,8 43,6 51,5

535 312,5 129,6 62,9 43,6 51,6

540 312,5 129,7 63,0 43,7 51,6

545 312,6 129,7 63,1 43,8 51,7

550 312,7 129,8 63,1 43,9 51,7

555 312,7 129,9 63,2 43,9 51,8

560 312,8 130,0 63,3 44,0 51,8

565 312,9 130,1 63,4 44,0 51,9

570 312,9 130,1 63,4 44,1 51,9

575 313,0 130,2 63,5 44,2 52,0

580 313,0 130,3 63,6 44,2 52,0

585 313,1 130,3 63,6 44,3 52,0

590 313,1 130,4 63,7 44,3 52,1

595 313,2 130,5 63,7 44,4 52,1

600 313,3 130,5 63,8 44,4 52,2

605 313,3 130,6 63,9 44,5 52,2

610 313,3 130,6 63,9 44,5 52,2

615 313,4 130,7 64,0 44,6 52,3

620 313,4 130,7 64,0 44,6 52,3

625 313,5 130,8 64,1 44,7 52,3

630 313,5 130,8 64,1 44,7 52,4

635 313,6 130,9 64,2 44,8 52,4

640 313,6 130,9 64,2 44,8 52,4

645 313,6 131,0 64,3 44,8 52,5

650 313,7 131,0 64,3 44,9 52,5

655 313,7 131,1 64,4 44,9 52,5

660 313,8 131,1 64,4 44,9 52,6

665 313,8 131,2 64,4 45,0 52,6

670 313,8 131,2 64,5 45,0 52,6

675 313,9 131,2 64,5 45,0 52,6

680 313,9 131,3 64,5 45,1 52,7

685 313,9 131,3 64,6 45,1 52,7

690 313,9 131,3 64,6 45,1 52,7

695 314,0 131,4 64,7 45,2 52,7

700 314,0 131,4 64,7 45,2 52,8

705 314,0 131,4 64,7 45,2 52,8

710 314,1 131,5 64,7 45,3 52,8

715 314,1 131,5 64,8 45,3 52,8

720 314,1 131,5 64,8 45,3 52,9

725 314,1 131,6 64,8 45,3 52,9

730 314,1 131,6 64,9 45,4 52,9

735 314,2 131,6 64,9 45,4 52,9

740 314,2 131,6 64,9 45,4 52,9

745 314,2 131,7 64,9 45,4 52,9

750 314,2 131,7 65,0 45,5 53,0

755 314,3 131,7 65,0 45,5 53,0

760 314,3 131,7 65,0 45,5 53,0

765 314,3 131,8 65,0 45,5 53,0

770 314,3 131,8 65,1 45,5 53,0

775 314,3 131,8 65,1 45,6 53,0

780 314,3 131,8 65,1 45,6 53,1

785 314,4 131,8 65,1 45,6 53,1

790 314,4 131,9 65,1 45,6 53,1

795 314,4 131,9 65,2 45,6 53,1

800 314,4 131,9 65,2 45,6 53,1

805 314,4 131,9 65,2 45,7 53,1

810 314,4 131,9 65,2 45,7 53,1

815 314,4 131,9 65,2 45,7 53,1

820 314,5 132,0 65,2 45,7 53,2

825 314,5 132,0 65,3 45,7 53,2

830 314,5 132,0 65,3 45,7 53,2

835 314,5 132,0 65,3 45,7 53,2

840 314,5 132,0 65,3 45,8 53,2

845 314,5 132,0 65,3 45,8 53,2

850 314,5 132,0 65,3 45,8 53,2

855 314,5 132,1 65,3 45,8 53,2

860 314,6 132,1 65,4 45,8 53,2

865 314,6 132,1 65,4 45,8 53,2

870 314,6 132,1 65,4 45,8 53,3

875 314,6 132,1 65,4 45,8 53,3

880 314,6 132,1 65,4 45,8 53,3

885 314,6 132,1 65,4 45,9 53,3

890 314,6 132,1 65,4 45,9 53,3

895 314,6 132,1 65,4 45,9 53,3

900 314,6 132,2 65,4 45,9 53,3

905 314,6 132,2 65,5 45,9 53,3

910 314,6 132,2 65,5 45,9 53,3

915 314,7 132,2 65,5 45,9 53,3

920 314,7 132,2 65,5 45,9 53,3

925 314,7 132,2 65,5 45,9 53,3

930 314,7 132,2 65,5 45,9 53,3

935 314,7 132,2 65,5 45,9 53,3

940 314,7 132,2 65,5 45,9 53,3

945 314,7 132,2 65,5 46,0 53,4

950 314,7 132,2 65,5 46,0 53,4

955 314,7 132,2 65,5 46,0 53,4

960 314,7 132,3 65,5 46,0 53,4

965 314,7 132,3 65,6 46,0 53,4

970 314,7 132,3 65,6 46,0 53,4

975 314,7 132,3 65,6 46,0 53,4

980 314,7 132,3 65,6 46,0 53,4

985 314,7 132,3 65,6 46,0 53,4

990 314,7 132,3 65,6 46,0 53,4

995 314,7 132,3 65,6 46,0 53,4

1000 314,8 132,3 65,6 46,0 53,4

1005 314,8 132,3 65,6 46,0 53,4

1010 314,8 132,3 65,6 46,0 53,4

1015 314,8 132,3 65,6 46,0 53,4

1020 314,8 132,3 65,6 46,0 53,4

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

VALVOLA DI MOTORE A SCOPPIO

ELABORAZIONE CON METODO CRANK-NICOLSON E MATRICE TRIDIAGONALE

DATI CALCOLO COSTANTI E PARAMETRI

0,005263157895

m ALFA TETAC TETAM

L 0,1 m lunghezza valvola 5 ∆x

d 0,009 m diametro valvola 6 Nt 1024 adimensionale numero punti reticolo temporale ( arrot.) 1,122155633 0,05847953216 0,03898635478

Nx 20 adim numero punti reticolo x 7 D = K/(ρc) 3,24E-06 m^2/s diffusività termica

1024 s durata temporale integrazione 8 G = 4γa/(ρcd) 5,33E-03 1/s convettività laterale

τ 1,0 s passo temporale 9 μ = G∆t 5,33E-03 adimensionale parametro

∆t

T0 20 °C temperatura iniziale della valvola 10 = 5,85E-02 adimensionale coefficiente termico lato carter

θc γc*∆x/K

Ta 20 °C temperatura miscela alimentazione 11 = 3,90E-02 adimensionale coefficiente termico lato cilindro motore

θm γm*∆x/K

Tm 1300 °C temperatura media gas nel cilindro 12 = 0,5*D*Δt/(Δx)^2 5,84E-02 adimensionale parametro CN tridiagonale

λ

Tc 80 °C temperatura olio nel carter distribuzione 13 = 1 + 2λ + μ 1,12E+00 adimensionale parametro CN tridiagonale

α

50 W/(m^2*°K)coefficiente scambio convettivo valvola-miscela alimentazione 14

γa 100 W/(m^2*°K)coefficiente scambio convettivo valvola cilindro motore 15

γm 150 W/(m^2*°K)coefficiente scambio convettivo valvola olio carter distribuzione 16

γc 8100 kg/m^3 densità valvola 17

ρ

K 13,5 W/(m*°K) conduttività valvola 18

c 515 W*s/(kg*°K)calore specifico a p costante valvola 19

Andamento della temperatura in funzione della ascissa x e del tempo t

i 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

x (m) 0 0,005 0,011 0,016 0,021 0,026 0,032 0,037 0,042 0,047 0,053 0,058 0,063 0,068 0,074 0,079 0,084 0,089 0,095 0,100

t (s) j Tc sfera

0,00 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20

2,00 70,57 22,64 20,14 20,01 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,01 20,18 23,49

3,00 75,38 27,63 20,65 20,05 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,04 20,53 23,81

4,00 79,69 32,11 21,55 20,15 20,01 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,01 20,11 20,83 24,10

5,00 83,59 36,17 22,72 20,34 20,04 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,02 20,19 21,11 24,37

6,00 87,17 39,89 24,06 20,63 20,08 20,01 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,01 20,04 20,28 21,37 24,61

7,00 90,47 43,32 25,53 21,01 20,15 20,02 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,01 20,07 20,38 21,60 24,83

8,00 93,54 46,50 27,08 21,47 20,25 20,04 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,02 20,10 20,49 21,82 25,03

9,00 96,41 49,48 28,67 22,01 20,38 20,06 20,01 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,03 20,14 20,60 22,02 25,22

10,00 99,11 52,29 30,28 22,62 20,55 20,10 20,02 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,01 20,04 20,18 20,71 22,21 25,40

11,00 101,65 54,93 31,89 23,28 20,75 20,15 20,03 20,00 20,00 20,00 20,00 20,00 20,00 20,00 20,01 20,05 20,23 20,82 22,39 25,57

12,00 104,07 57,44 33,51 23,99 20,99 20,21 20,04 20,01 20,00 20,00 20,00 20,00 20,00 20,00 20,01 20,07 20,27 20,93 22,56 25,74

13,00 106,37 59,83 35,11 24,75 21,26 20,29 20,06 20,01 20,00 20,00 20,00 20,00 20,00 20,00 20,02 20,09 20,33 21,04 22,72 25,89

14,00 108,56 62,11 36,69 25,54 21,56 20,38 20,08 20,02 20,00 20,00 20,00 20,00 20,00 20,01 20,03 20,11 20,38 21,14 22,88 26,03

15,00 110,66 64,29 38,25 26,36 21,89 20,49 20,11 20,02 20,00 20,00 20,00 20,00 20,00 20,01 20,03 20,13 20,44 21,25 23,02 26,17

16,00 112,67 66,38 39,79 27,20 22,25 20,61 20,15 20,03 20,01 20,00 20,00 20,00 20,00 20,01 20,04 20,15 20,49 21,35 23,17 26,31

17,00 114,60 68,39 41,31 28,06 22,64 20,76 20,19 20,04 20,01 20,00 20,00 20,00 20,00 20,01 20,05 20,18 20,55 21,46 23,30 26,43

18,00 116,47 70,33 42,79 28,94 23,05 20,91 20,24 20,06 20,01 20,00 20,00 20,00 20,00 20,02 20,06 20,21 20,61 21,56 23,43 26,56

19,00 118,27 72,19 44,25 29,82 23,48 21,09 20,30 20,08 20,02 20,00 20,00 20,00 20,01 20,02 20,07 20,24 20,67 21,66 23,56 26,67

20,00 120,00 74,00 45,68 30,72 23,93 21,28 20,37 20,10 20,02 20,01 20,00 20,00 20,01 20,03 20,09 20,27 20,73 21,75 23,68 26,79

21,00 121,68 75,74 47,09 31,61 24,40 21,48 20,45 20,12 20,03 20,01 20,00 20,00 20,01 20,03 20,10 20,30 20,79 21,85 23,79 26,90

22,00 123,31 77,44 48,47 32,52 24,89 21,70 20,53 20,15 20,04 20,01 20,00 20,00 20,01 20,04 20,12 20,33 20,86 21,94 23,91 27,01

23,00 124,89 79,08 49,82 33,42 25,38 21,93 20,62 20,18 20,05 20,01 20,00 20,00 20,01 20,04 20,13 20,37 20,92 22,03 24,02 27,11

24,00 126,42 80,67 51,15 34,32 25,90 22,18 20,73 20,22 20,06 20,02 20,00 20,00 20,02 20,05 20,15 20,40 20,98 22,12 24,12 27,21

25,00 127,91 82,22 52,45 35,22 26,42 22,44 20,84 20,26 20,07 20,02 20,01 20,01 20,02 20,06 20,17 20,44 21,04 22,21 24,23 27,31

26,00 129,36 83,72 53,73 36,12 26,95 22,71 20,96 20,31 20,09 20,03 20,01 20,01 20,02 20,07 20,19 20,47 21,10 22,30 24,33 27,40

27,00 130,77 85,19 54,98 37,02 27,49 22,99 21,08 20,36 20,11 20,03 20,01 20,01 20,03 20,07 20,20 20,51 21,16 22,38 24,42 27,49

28,00 132,14 86,61 56,21 37,91 28,04 23,28 21,22 20,41 20,13 20,04 20,01 20,01 20,03 20,08 20,22 20,55 21,22 22,46 24,52 27,58

29,00 133,48 88,00 57,41 38,79 28,60 23,58 21,36 20,48 20,15 20,05 20,02 20,01 20,03 20,09 20,24 20,59 21,28 22,54 24,61 27,67

30,00 134,79 89,36 58,60 39,67 29,16 23,89 21,52 20,54 20,18 20,06 20,02 20,02 20,04 20,10 20,27 20,62 21,34 22,62 24,70 27,76

31,00 136,06 90,68 59,76 40,54 29,72 24,21 21,67 20,61 20,21 20,07 20,02 20,02 20,04 20,11 20,29 20,66 21,40 22,70 24,79 27,84

32,00 137,31 91,98 60,90 41,41 30,29 24,54 21,84 20,69 20,24 20,08 20,03 20,02 20,05 20,13 20,31 20,70 21,46 22,78 24,87 27,92

33,00 138,52 93,24 62,03 42,27 30,86 24,88 22,02 20,77 20,27 20,09 20,03 20,03 20,05 20,14 20,33 20,74 21,51 22,85 24,96 28,00

34,00 139,71 94,48 63,13 43,12 31,44 25,22 22,20 20,85 20,31 20,11 20,04 20,03 20,06 20,15 20,36 20,78 21,57 22,93 25,04 28,08

35,00 140,88 95,69 64,21 43,96 32,01 25,57 22,38 20,94 20,35 20,12 20,05 20,04 20,07 20,16 20,38 20,82 21,63 23,00 25,12 28,15

36,00 142,02 96,87 65,28 44,80 32,59 25,92 22,58 21,04 20,39 20,14 20,05 20,04 20,08 20,18 20,40 20,86 21,68 23,07 25,20 28,23

37,00 143,13 98,03 66,32 45,63 33,17 26,28 22,78 21,14 20,44 20,16 20,06 20,05 20,08 20,19 20,43 20,90 21,74 23,14 25,27 28,30

38,00 144,22 99,16 67,35 46,45 33,75 26,64 22,98 21,25 20,49 20,18 20,07 20,05 20,09 20,21 20,45 20,94 21,80 23,21 25,35 28,37

39,00 145,29 100,27 68,36 47,26 34,33 27,01 23,19 21,35 20,54 20,20 20,08 20,06 20,10 20,22 20,48 20,97 21,85 23,27 25,42 28,44

40,00 146,34 101,36 69,36 48,06 34,90 27,38 23,41 21,47 20,59 20,23 20,09 20,07 20,11 20,23 20,50 21,01 21,90 23,34 25,49 28,50

41,00 147,37 102,43 70,33 48,86 35,48 27,76 23,63 21,59 20,65 20,25 20,11 20,07 20,12 20,25 20,53 21,05 21,96 23,41 25,56 28,57

42,00 148,38 103,48 71,30 49,64 36,06 28,14 23,86 21,71 20,71 20,28 20,12 20,08 20,13 20,27 20,55 21,09 22,01 23,47 25,63 28,64

43,00 149,37 104,51 72,24 50,42 36,63 28,52 24,09 21,84 20,78 20,31 20,13 20,09 20,14 20,28 20,58 21,13 22,06 23,53 25,70 28,70

44,00 150,34 105,52 73,17 51,19 37,20 28,90 24,32 21,97 20,84 20,35 20,15 20,10 20,15 20,30 20,61 21,17 22,11 23,59 25,77 28,76

45,00 151,29 106,51 74,09 51,95 37,77 29,29 24,56 22,10 20,91 20,38 20,17 20,11 20,16 20,32 20,63 21,21 22,16 23,66 25,83 28,82

46,00 152,23 107,48 74,99 52,71 38,34 29,68 24,80 22,24 20,99 20,42 20,19 20,13 20,17 20,33 20,66 21,25 22,21 23,72 25,89 28,88

47,00 153,15 108,44 75,88 53,45 38,91 30,07 25,05 22,38 21,06 20,45 20,20 20,14 20,19 20,35 20,69 21,28 22,26 23,77 25,96 28,94

48,00 154,05 109,37 76,76 54,19 39,47 30,46 25,30 22,53 21,14 20,49 20,23 20,15 20,20 20,37 20,71 21,32 22,31 23,83 26,02 29,00

49,00 154,94 110,30 77,62 54,92 40,03 30,85 25,55 22,68 21,22 20,54 20,25 20,16 20,21 20,39 20,74 21,36 22,36 23,89 26,08 29,06

50,00 155,81 111,20 78,47 55,64 40,59 31,25 25,81 22,83 21,31 20,58 20,27 20,18 20,23 20,41 20,77 21,40 22,41 23,95 26,14 29,11

51,00 156,67 112,10 79,31 56,35 41,14 31,64 26,06 22,99 21,39 20,63 20,30 20,19 20,24 20,43 20,79 21,43 22,46 24,00 26,20 29,17

52,00 157,51 112,97 80,13 57,06 41,69 32,04 26,32 23,14 21,48 20,68 20,32 20,21 20,26 20,44 20,82 21,47 22,51 24,05 26,25 29,22

53,00 158,34 113,83 80,94 57,76 42,24 32,43 26,59 23,31 21,58 20,73 20,35 20,23 20,27 20,46 20,85 21,51 22,55 24,11 26,31 29,28

54,00 159,16 114,68 81,75 58,45 42,79 32,83 26,85 23,47 21,67 20,78 20,38 20,25 20,29 20,48 20,88 21,54 22,60 24,16 26,36 29,33

55,00 159,96 115,52 82,53 59,13 43,33 33,22 27,12 23,64 21,77 20,83 20,41 20,27 20,30 20,50 20,90 21,58 22,64 24,21 26,42 29,38

56,00 160,75 116,34 83,31 59,80 43,87 33,62 27,39 23,81 21,87 20,89 20,44 20,29 20,32 20,53 20,93 21,62 22,69 24,26 26,47 29,43

57,00 161,53 117,15 84,08 60,47 44,40 34,02 27,66 23,98 21,97 20,95 20,47 20,31 20,34 20,55 20,96 21,65 22,73 24,32 26,52 29,48

Dettagli
Publisher
_stan
34 pagine
1 download