Tre amici studenti, Franco, Roberto, Marco, decidono di fare una camminata in montagna. Giunti in auto alle pendici montuose, iniziano una salita lunga e ripida. Al termine si trovano su di un grande altipiano. Splendidi prati e rocce, un ruscello. Aria fresca e pulita, grande silenzio. Lunga e piacevole passeggiata. Sulla via del ritorno li coglie il temporale. Pioggia forte e calo immediato della temperatura. I tre malcapitati non sono attrezzati a difendersi dalla pioggia.
Non rimane loro che marciare lungo i prati ormai ridotti ad una melma scivolosa.
Dopo più di un'ora, inzuppati sino alle ossa, giungono all'auto. Dove ci saranno abiti di ricambio, coperte, generi di conforto? Nulla di tutto questo. Non resta che salire in auto e tornare mestamente in città battendo i denti. Evidentemente i tre ignorano la legge di Murphy. Una giornata da dimenticare.Dopo alcuni decenni i tre ancora ricordano quel dolente pomeriggio. Uno di loro, un po' maniaco di matematica e fisica, ripensa alla pioggia presa e comincia a riflettere. Si poteva forse prenderne meno correndo più veloci?
In generale: una persona sotto la pioggia corre verso un riparo. La sua velocità influenza la quantità di pioggia che prenderà? Consultare il web è rapido. In breve si scopre che il problema è un classico, studiato ormai da cervelli fini (A. De Angelis, Eur. Phys., 1987, 8, 201-202). Un fisico americano ha perfino creato un'applet che calcola la quantità di pioggia presa in funzione della velocità (http://www.dctech.com/physics/notes/0006.php).
Rivediamo la soluzione, limitandoci a considerare il caso di assenza di vento, quindi di una pioggia che cade verticalmente. L'uomo viene schematizzato come un parallelepipedo. La faccia superiore, perpendicolare alla pioggia sia So (superficie orizzontale) e rappresenta testa e spalle, la faccia frontale sia Sv (superficie verticale). Per effetto del moto relativo l'uomo in corsa riceve la pioggia obliquamente.
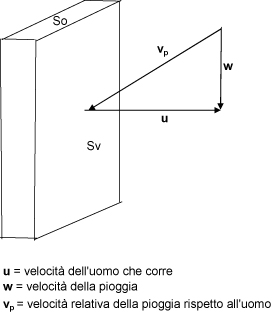
Le grandezze da considerare sono la velocità di caduta della pioggia (w), la velocità dell'uomo che corre (u), l'intensità della pioggia (I), la distanza (L) dal riparo, il volume di pioggia assorbita dall'uomo (V).
L'intensità (media) della pioggia si misura in mm/h e dunque è il rapporto tra la colonna di acqua che cade su di una qualsiasi superficie durante la pioggia e la durata della pioggia. La velocità relativa della pioggia (vettore vp ) si ottiene sommando i vettori velocità con la regola del parallelogramma: vp = w - u
Le fonti citate forniscono la soluzione:
Consideriamo u come unica variabile indipendente, mentre le altre sono assunte come parametri. Si vede immediatamente che V ha andamento iperbolico in funzione di u. La funzione V è sempre decrescente (derivata prima negativa). Quando u tende all'infinito V tende all'asintoto:
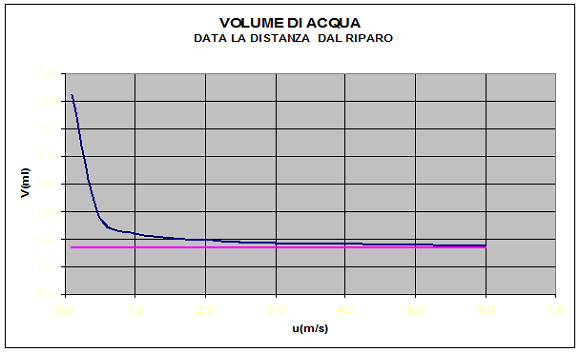
Conclusione: quanto più grande è u, ossia quanto più si corre, tanto minore è la quantità di pioggia assorbita. Ed anche: se due runner decidono di sfidarsi in una gara su un percorso assegnato, in caso di pioggia il più veloce dei due si bagna di meno.
Bene, ora vogliamo riproporre il problema in termini un pò diversi.
Piero e Giorgio, durante una passeggiata in pianura vengono colti dalla pioggia, che cade verticalmente. Piero, molto istintivo, propone di correre alla ricerca di un riparo. Giorgio, super-razionale, consiglia invece di restare immobili fin tanto che spiove; egli pensa che si tratti di una breve pioggia estiva che si risolverà in una decina di minuti. Correndo, egli immagina, si prenderà molta più pioggia, per effetto della velocità relativa. I due amici, inoltre, non sono a conoscenza di eventuali ripari dalla pioggia. Potrebbe non essercene per molti chilometri. I diversi punti di vista dei due amici non trovano un compromesso. Essi concordano allora che Piero correrà lungo il sentiero alla ricerca di un riparo, se esiste, dove fermarsi. In assenza di riparo, al termine della pioggia comunque si fermerà ad attendere l'amico. Giorgio, invece, resterà immobile sino a che spiove, poi riprenderà a camminare per raggiungere Piero.
Domanda 1 Chi dei due si bagna di più? Considerare i diversi possibili casi. Scrivere le equazioni che identificano il volume di pioggia assorbito da entrambi gli amici. Trarre le considerazioni opportune.
Domanda 2 Assumiamo che Piero non trovi riparo e che sia: So = 0,1 m2 , Sv = 0,6 m2 , t = 0,5 h la durata delle pioggia, u = 5 m/s, w = 2,5 m/s, I = 2 mm/h. Calcolare, con le formule di cui a Risposta 1, i volumi di pioggia assorbiti dai due amici e la durata della corsa di Piero.
Domanda 3 Assumiano che Piero trovi riparo dopo un tempo tr = 0,5 h e che sia: So = 0,1 m2 , Sv = 0,6 m2, t = 2h, u = 2 m/s, w = 4 m/s, I = 7 mm/h. Calcolare i volumi assorbiti dai due amici e la durata della corsa di Piero.
Domanda 4 Assumiano che Piero trovi riparo dopo un tempo tr = 0,5 h e che sia: So = 0,1 m2 , Sv = 0,6 m2, t = 2h, u = 1 m/s, w = 8 m/s, I = 8,5 mm/h. Calcolare i volumi assorbiti dai due amici e la durata della corsa di Piero.
La soluzione sarà pubblicata la prossima settimana
Intanto puoi inserire dei commenti per chiedere chiarimenti o dare la tua risposta.
Riferimenti
(1) A. De Angelis - Eur. Phys. 1987, 8, 201 - 202
(2) http://www.dctech.com/physics/notes/0006.php
Risposta 1
Cominciamo a renderci conto che esistono due possibilità: caso1: Piero non trova riparo, caso 2: Piero trova riparo.
Caso 1: non esiste riparo. Prendiamo in considerazione la formula (a). Essa si applica alla corsa di Piero, a patto introdurre una piccola modifica. La formula, nei termini scritti, contiene la distanza L dal riparo, ma Piero in questo caso non trova riparo. Per adattarla al caso occorre allora porre:
L = ut
dove t è la durata della pioggia, che coincide con la durata della corsa di Piero.
Quindi la (a) diventa:
V = Iu(So/u + Sv/w)t = I(So +u/w Sv )t (b)
La formula (b) definisce la quantità di pioggia che Piero prende correndo per un intervallo di tempo t alla velocità u.
Quanta pioggia prende Giorgio? Per rispondere basta notare che Giorgio, avendo deciso di rimanere immobile si comporta esattamente come un pluviometro(*). Il volume di acqua che prende è dato da:
V' = I So t (c)
Infatti V' rappresenta il volume di acqua che si accumula in un pluviometro di sezione So nel tempo t. Notiamo che la (c) non è altro che la (b) quando u = 0 Se dividiamo la (b) per la (c) otteniamo:
V/V' = 1+ u/w* Sv/ So (d)
Il secondo membro è chiaramente > 1, dunque risulta V > V'
Concludiamo che, in questo Caso 1, Piero (l'uomo che corre) si bagna di più di Giorgio (l'uomo che resta immobile), per qualsiasi valore del rapporto u/w.
Caso 2: Piero trova riparo
Qui la situazione è diversa in quanto esistono due diverse durate di tempo: t la durata della pioggia tr la durata di tempo necessaria a Piero per raggiungere il riparo. E chiaramente: tr
Dunque Piero raggiunge il riparo prima che termini di piovere. Possiamo allora riscrivere le equazioni (b) e (c), ma questa volta con durate di tempo diverse.
V = I(So +u/w Sv ) tr (e)
V' = I So t (f)
Ed ancora, dividendo la prima per la seconda:
V/V' = (1+ u/w* Sv/ So) tr /t
Qui abbiamo, a secondo membro:
(1+ u/w* Sv/ So) >1 tr /t
In conclusione il rapporto V/V' , dato dal prodotto dei due termini, può essere maggiore o minore di 1. Di conseguenza è possibile che si bagni di più l'uomo che corre oppure quello che sta immobile, secondo i valori dei parametri u/w e tr/t.
Vediamo una rappresentazione geometrica del Caso 2.
Possiamo riscrivere la formula in questo modo: V/ V' = (a + b u/w) dove: 0
Che nel piano di coordinate (u/w, V/V') rappresenta un fascio di rette uscenti dal punto (0, a), tutte con coefficiente angolare positivo. Tale fascio incontra la retta orizzontale V/ V'=1 nel punto:
(u/w)* = (1 - a)/b = So/Sv( tr/t - 1)
E dunque, una volta assegnato il rapporto t/tr, che individua la retta del fascio corrispondente, quando u/w (u/w)* si verifica esattamente l'opposto.
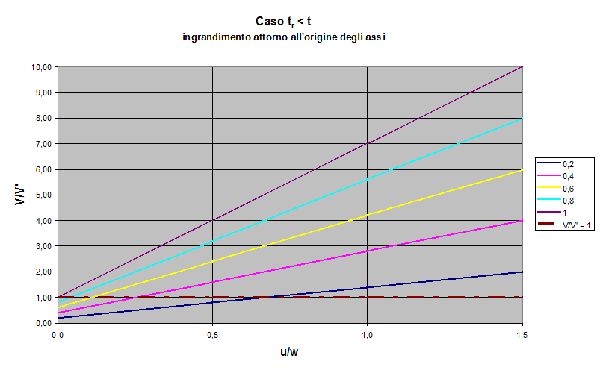
Teniamo presente che le velocità u e w hanno dei limiti fisici: 0
Anche l'intensità della pioggia ha dei limiti fisici: 1
Finora abbiamo assunto l'ipotesi implicita che il parametro Sv/So abbia lo stesso valore per Piero e Giorgio. Tuttavia nel caso che l'uno fosse smilzo, l'altro obeso, il rapporto sarebbe un po' diverso e le formule (c)+(d) ed anche (d)+(e) dovrebbero riportare due valori diversi per il rapporto delle superfici.
Le risposte alle domande 2, 3, 4 sono riportate nel file EXCEL allegato>>>.
Hume



