[math]\frac{25}{12}[/math]
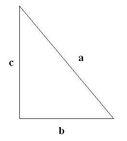
. Sapendo che l'ipotenusa è lunga 15, determinare la lunghezza dei cateti.
Siano
[math]a[/math]
e [math]b[/math]
i cateti, [math]c[/math]
l'ipotenusa, [math]h[/math]
l'altezza relativa all'ipotenusa.Per i teoremi sui triangoli rettangoli, sappiamo che cateti e tangente dell'angolo sono legati in questo modo
[math]a=b\tan\alpha[/math]
[math]b=a\tan\beta[/math]
Perciò risulta essere
[math]\tan\alpha=\frac{a}{b}[/math]
[math]\tan\beta=\frac{b}{a}[/math]
Nel nostro problema abbiamo
[math]\tan\alpha+\tan\beta=\frac{25}{12}[/math]
ovvero
[math]\frac{a}{b}+\frac{b}{a}=\frac{25}{12}[/math]
che possiamo anche scrivere
[math]\frac{a^2+b^2}{ab}=\frac{25}{12}[/math]
(1)
Essendo però il nostro un triangolo rettangolo, sussiste il teorema ti pitagora che ci dice
[math]a^2+b^2=15^2[/math]
(2)
Mettiamo a sistema la (1) e la (2) ottenendo
[math]\begin{cases} \frac{a^2+b^2}{ab}=\frac{25}{12} \\ a^2+b^2=225 \end{cases}[/math]
Questo è un sistema simmetrico a due incognite.
Se non si ricorda come trattare questo tipo di sistema, nella sezione "Sistemi" c'è un esempio con lo svolgimento.
Sostituendo il valore di
[math]a^2+b^2[/math]
nella prima equazione, si avrà[math]\begin{cases} \frac{225}{ab}=\frac{25}{12} \\ a^2+b^2=225 \end{cases}[/math]
ovvero
[math]\begin{cases} \frac{225}{ab}=\frac{25}{12} \\ a^2+b^2=225 \end{cases}[/math]
trovando il valore di
[math]ab[/math]
e ricordando l'identità [math]a^2+b^2=(a+b)^2-2ab[/math]
si ha[math]\begin{cases} ab=108 \\ (a+b)^2-2ab=225 \end{cases}[/math]
sapendo che
[math]ab=108[/math]
la seconda equazione diventa[math]\begin{cases} ab=108 \\ (a+b)^2=225+216=441=21^2 \end{cases}[/math]
Perciò si ottiene
[math]\begin{cases} ab=108 \\ a+b=+-21 \end{cases}[/math]
Ma dobbiamo escludere il caso in cui la somma è
[math]-21[/math]
perchè sia [math]a[/math]
che [math]b[/math]
sono positivi, in quanto misure di segmenti.Ora impostiamo l'equazione che ci fornisce le due soluzioni
[math]x^2-sx+p=0[/math]
dove [math]s[/math]
è la somma delle due radici e
[math]p[/math]
il prodotto.[math]x^2-21x+108=0[/math]
Le soluzioni sono
[math]x_1=a=12[/math]
[math]x_2=b=9[/math]
valori che corrispondono alla lunghezza dei due lati cercati.
FINE
