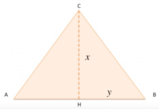
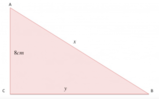
[math]ABC[/math]
si ha [math]a=60 cm[/math]
, [math]b=45 cm[/math]
, [math]c=30 cm[/math]
. La bisettrice dell'angolo in [math]B[/math]
incontra il lato opposto nel punto [math]D[/math]
; traccia la parallela ad [math]AB[/math]
passante per [math]D[/math]
e determina le lunghezza dei segmenti in cui essa divide il lato [math]BC[/math]
.

Svolgimento
Chiamiamo con le incognite[math]x[/math]
e [math]y[/math]
i segmenti sul lato [math]AC[/math]
divisi dal punto [math]D[/math]
:
[math]AD = x [/math]
[math]DC = y [/math]
Sapendo che il lato
[math]AC[/math]
, cioè [math]b[/math]
, misura [math]45 cm[/math]
, possiamo dire che:
[math]x + y = 45[/math]
Cerchiamo ora di impostare un'altra equazione in
[math]x[/math]
e [math]y[/math]
in modo da poter formare un sistema.Sappiamo che, secondo il teorema della bisettrice, la bisettrice di un angolo interno di un triangolo divide il lato opposto in parti proporzionali ai lati adiacenti; quindi:
[math] AD : DC = AB : BC [/math]
[math] x : y = 30 : 60 [/math]
[math] 60x = 30y [/math]
Impostiamo quindi il sistema:
[math][/math]
left{ \begin{array}{rl}
x + y = 45 &\
60 x = 30y &
end{array}\right.
[math][/math]
left{ \begin{array}{rl}
x + y = 45 &\
60 x = 30y &
end{array}\right.
[math][/math]
Ricaviamo un'incognita dalla prima equazione e risolviamo per sostituzione:
[math][/math]
left{ \begin{array}{rl}
x = 45 - y &\
60 x = 30y &
end{array}\right.
[math][/math]
left{ \begin{array}{rl}
x = 45 - y &\
60 x = 30y &
end{array}\right.
[math][/math]
Lavoriamo sulla seconda equazione:
[math] 60 (45 - y) = 30 y [/math]
[math] 2700 - 60y - 30 y = 0 [/math]
[math] - 90y = - 2700 \to y = 30 [/math]
Il corrispondente valore di
[math]x[/math]
è :
[math] x = 45 - y = 45 - 30 = 15 [/math]
Ora consideriamo i triangoli
[math]ABC [/math]
e [math]DCE[/math]
. Essi sono simili, poiché quando si traccia in un triangolo la parallela ad un lato che interseca gli altri due in due punti, si forma un triangolo simile a quello di partenza; quindi possiamo mettere i loro lati in proporzione:
[math] AC : DC = BC : EC [/math]
[math] 45 : 15 = 60 : EC [/math]
[math] EC = frac(60 \cdot 15)(45) = 20 cm [/math]
Troviamo ora il segmento
[math]BE[/math]
per differenza:
[math]BE = BC - EC = 60 - 20 = 40 cm [/math]