(50 punti)

8' di lettura

3 / 5 (1)

In questo appunto si descrive il rombo e si riportano alcuni problemi svolti. Spesso la risoluzione di un problema di geometria richiede l’aiuto dell’algebra. Una volta individuate le incognite del problema è possibile utilizzare le equazioni di primo o secondo grado per arrivare alla soluzione. Nel problema proposto la figura geometrica in questione è un rombo di cui è nota l’area e la relazione esistente tra le misure delle sue diagonali, entrambe incognite.

Per risolvere il problema utilizzeremo un’equazione di secondo grado e anche il teorema di Pitagora. Come sempre apriamo l’appunto con un ripasso teorico sempre utile.

Definizione e proprietà del rombo

Il rombo è un poligono convesso con i lati congruenti e paralleli.
Il rombo è un parallelogramma che ha i lati congruenti.
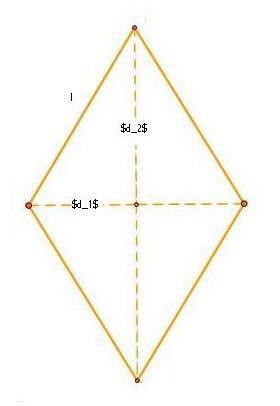
Le diagonali del rombo non sono congruenti, sono perpendicolari e si intersecano nel loro punto medio. Ogni diagonale è anche bisettrice degli angoli interni.
Per il rombo vale il seguente teorema: “in un rombo le diagonali sono perpendicolari fra loro e sono bisettrici degli angoli interni”.
In generale gli angoli non sono retti, se non per quei rombi particolari che sono i quadrati, ma sono due acuti (di ampiezza inferiore a 90°) e due ottusi (di ampiezza superiore a 90° e inferiore a 180°).
Gli angoli interni opposti sono congruenti.

Diagonali e simmetria

Le due diagonali dividono il rombo in quattro triangoli rettangoli congruenti.
Ciascuna diagonale divide anche il rombo in due triangoli, ciascuno dei quali è un triangolo isoscele e dunque congruenti.
Le diagonali del rombo sono anche assi di simmetria per la figura, e il loro punto di intersezione è un centro di simmetria.
Se prendiamo in esame un rombo è una sua diagonale e consideriamo uno dei due triangoli che si ottengono e lo ruotiamo di 180° intorno al punto centrale, questo triangolo va a sovrapporsi esattamente all’altro.
Poiché nel rombo le somme dei lati opposti sono congruenti questo quadrilatero può essere circoscritto ad un cerchio, ovvero il rombo è un quadrilatero che ammette la circonferenza inscritta. Il raggio della circonferenza inscritta è detto anche apotema e coincide con l’altezza relativa al lato obliquo.
Un quadrilatero può essere inscritto in una circonferenza se e solo se due angoli opposti sono supplementari; sono sempre inscrivibili il quadrato, il rettangolo e il trapezio isoscele. Il rombo non è iscrivibile perché le due coppie di angoli opposti non sono supplementari.

Quadrilateri equiscomponibili a rettangoli

Per il calcolo dell’area di una superficie piana rivediamo la definizione di figura equiscomponibile
In geometria due figure si dicono equiscomponibili se si possono scomporre in modo che ogni parte della prima figura sia congruente a una parte della seconda figura e viceversa.
Sappiamo infatti che ogni triangolo è scomponibile a un rettangolo che ha la stessa base e metà altezza del triangolo, oppure metà base e la stessa altezza del triangolo.
Ogni rombo è equiscomponibile a un rettangolo che ha per base la diagonale maggiore del rombo e per altezza metà diagonale minore del rombo, oppure ha per base metà diagonale maggiore del rombo e per altezza la diagonale minore del rombo.
Anche nel rombo è possibile definire l’altezza relativa al lato come segmento perpendicolare al lato compreso tra un vertice opposto e la retta che contiene tale lato. Possiamo dire perciò che ogni rombo è equiscomponibile a un rettangolo che ha per base il lato del rombo e per altezza dell’altezza del rombo.
In generale ogni quadrilatero può essere trasformato in un rettangolo a esso equiscomponibile.
Due figure si dicono equivalenti se hanno la stessa estensione superficiale e quindi hanno la stessa area.
Due figure che hanno il perimetro della stessa lunghezza si dicono isoperimetriche e possono non essere equivalenti.
Per ulteriori approfondimenti sulle figure isoperimetriche vedi qua

Perimetro e area del rombo

Il perimetro del rombo si calcola moltiplicando per quattro la misura del suo lato:

[math]2p=4L[/math]

La misura del lato si ottiene dividendo per 4 quella del perimetro, oppure dividendo per 2 quella del semiperimetro

[math]L={2p \over 4}[/math]

[math]L={p \over 2}[/math]

Formule dell’area
Per quanto detto sulla equiscomponibilità di questa figura è possibile calcolare l’area del rombo in diversi modi:

Utilizzando la misura delle due diagonali
Utilizzando la misura del lato e l’altezza relativa ad esso
Utilizzando la misura del lato e quella del raggio della circonferenza inscritta

Vediamo le formule che servono
Formula dell’area con le diagonali
L’area si calcola come semiprodotto delle sue diagonali (D,d):

[math]A=\frac{D \cdot d}{2}[/math]

da questa formula diretta è possibile ricavare la misura di ciascuna delle due diagonali:

[math]D=\frac{2 \cdot A}{d}[/math]

[math]d=\frac{2 \cdot A}{D}[/math]

Formula con lato (L) e altezza (h) relativa ad esso

[math]A=L \cdot h[/math]

[math]L=\frac{A}{h}[/math]

[math]h=\frac{A}{L}[/math]

Formula con lato (L) e raggio (r) della circonferenza inscritta

[math]A=L \cdot 2r[/math]

[math]L=\frac{A}{2r}[/math]

[math]r=\frac{A}{2L}[/math]

Problema svolto con un equazione di secondo grado

L’area di un rombo è uguale a

[math]960 cm^2[/math]

, una diagonale è

[math]{15 \over 8}[/math]

dell'altra, trovare il perimetro del rombo.

Procedura di svolgimento
Scegliamo come incognita una diagonale ed esprimiamo anche la misura dell’altra in funzione della stessa incognita.
Utilizziamo la formula dell’area come semiprodotto delle due diagonali in modo tale da ottenere un’equazione di secondo grado.
L’equazione risolvente è di secondo grado pura, le cui soluzioni si ottengono estraendo la radice quadrata del rapporto tra il termine noto è il coefficiente del termine di secondo grado.
Trovato il valore dell’incognita x, abbiamo la misura delle due diagonali.
Ora dobbiamo determinare la misura del lato obliquo per poter calcolare il perimetro.
Applichiamo il teorema di Pitagora ad uno dei 4 triangoli individuati dall’intersezione delle due diagonali. In questo triangolo il lato obliquo è l’ipotenusa e i due cateti sono le semidiagonali.

Svolgiamo i calcoli.