Calcola l'area di un rettangolo in cui è noto che una dimensionesupera l'altra di
[math]38[/math]
e che la loro somma è [math]100[/math]
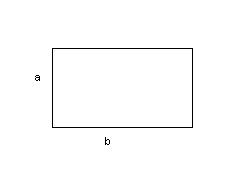 Dati
Dati
[math]b-a=38[/math]
[math]b+a=100[/math]
Svolgimento
Mettiamo a sistema le due equazioni note
[math]\begin{cases} b-a=38 \\ b+a=100 \ \end{cases}[/math]
Risolvendo il sistema avremo la misura dei due lati
[math]\begin{cases} b-a=38 \\ b+a=100 \ \end{cases}[/math]
; [math]\begin{cases} b=38+a \\ b+a=100 \ \end{cases}[/math]
;[math]\begin{cases} b=38+a \\ 38+a+a=100 \ \end{cases}[/math]
; [math]\begin{cases} b=38+a \\ 2a=62 \ \end{cases}[/math]
;[math]\begin{cases} b=69 \\ a=31 \ \end{cases}[/math]
.Pertanto
[math]A=b \cdot a=(31) \cdot (69)=2139[/math]
.