In un triangolo rettangolo i cateti hanno per somma
[math]80,5m[/math]
e uno è i [math]3/4[/math]
dell'altro.Determinare l'ipotenusa del triangolo
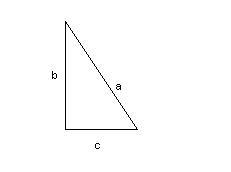 Dati
Dati[math]b+c=80,5m[/math]
[math]c=3/4b[/math]
Svolgimento
Mettiamo a sistema le due equazioni note
[math]\begin{cases} b+c=80.5 \\ c=3/4 b \ \end{cases}[/math]
Risolvendo il sistema avremo i valori di
[math]b[/math]
e [math]c[/math]
[math]\begin{cases} b+c=80.5 \\ c=3/4 b \ \end{cases}[/math]
; [math]\begin{cases} b+3/4b=80.5 \\ c=3/4 b \ \end{cases}[/math]
;
[math]\begin{cases} 7/4 b=80.5 \\ c=3/4 b \ \end{cases}[/math]
; [math]\begin{cases} b=(80.5) \cdot 4/7 \\ c=3/4 b \ \end{cases}[/math]
;[math]\begin{cases} b=46 \\ c=3/4 \cdot (46) \ \end{cases}[/math]
; [math]\begin{cases} b=46 \\ c=34.5 \ \end{cases}[/math]
.Pertanto
[math]b=46m[/math]
e [math]c=34,5m[/math]
.Per il teorema di pitagora
[math]a=\sqrt{b^2+c^2}=\sqrt((46m)^2+(34,5m)^2)=\sqrt(2116+1190,25)m=\sqrt(3306,25)m=57,5m[/math]
.