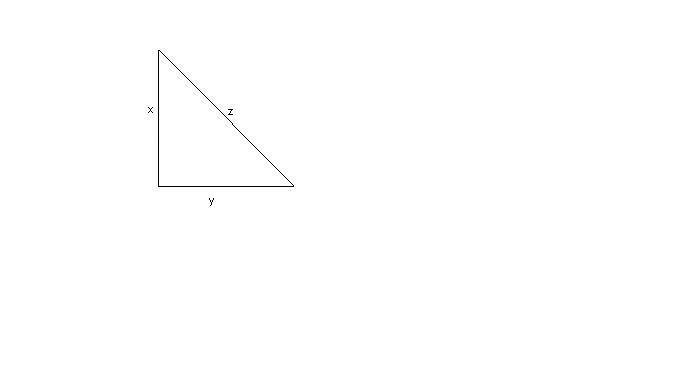Determina i cateti di un triangolo rettangolo sapendo che la loro somma è
[math]34cm[/math]
e che l'area del triangolo è
[math]120cm^2[/math]
.
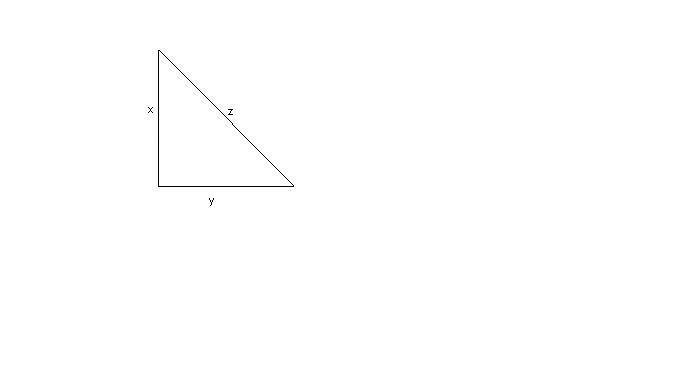
Svolgimento
Indicando con
[math]x[/math]
e
[math]y[/math]
i due cateti e con
[math]z[/math]
l'ipotenusa, i dati sono:
[math]x+y=34m ^^ A=120m^2[/math]
Noi sappiamo che
[math]A=(x \cdot y)/2=120m^2[/math]
Mettiamo a sistema le due
equazioni e procediamo nella risoluzione
[math]\begin{cases} (x \cdot y)/2=120 \\ x+y=34 \ \end{cases}[/math]
;
[math]\begin{cases} ((34-y)y)/2=120 \\ x=34-y \ \end{cases}[/math]
;
[math]\begin{cases} (34y-y^2)/2=120 \\ x=34-y \ \end{cases}[/math]
;
Il m.c.m., nella prima equazione, è
[math]2[/math]
quindi:
[math]\begin{cases} (34y-y^2-240)/2=0 \\ x=34-y \ \end{cases}[/math]
;
Dividendo ambo i membri della prima equazione per
[math]2[/math]
e cambiando di segno si ha:
[math]\begin{cases} y^2-34y+240=0 \\ x=34-y \ \end{cases}[/math]
;
Risolviamo l'equazione di secondo grado
[math]y^2-34y+240=0[/math]
[math](Delta/4)=(b/2)^2-ac=(-17)^2-((240) \cdot 1)=289-240=49[/math]
[math]y_(1,2)=((-b/2)+-\sqrt{(Delta/4)})/(a)=(17+-\sqrt(49))=(17+-7) => y_1=10 ^^ y_2=24[/math]
.
Pertanto
[math]\begin{cases} y_1=10 \\ x_1=34-y_1 \ \end{cases} => {(y_1=10),(x_1=24):}[/math]
;
[math]\begin{cases} y_2=24 \\ x_2=34-y_2 \ \end{cases} => {(y_2=24),(x_2=10):}[/math]
.
Quindi se scegliamo come cateto minore
[math]x[/math]
e come cateto maggiore
[math]y[/math]
, questi
misurano rispettivamente
[math]10cm[/math]
e
[math]24cm[/math]
; altrimenti viceversa.