Triangoli definizione e caratteristiche
Iniziamo la trattazione di questo argomento con alcune domande di pura curiosità matematica, legate ai triangoli:- Perché le strutture di alcuni palazzi hanno la forma di un triangolo?
- Quale tipo di triangolo può ricordare la forma della Sicilia?
- Come si può individuare il punto equidistante da tre piunti non allineati?
- Come capire dove costruire una piazza che abbia la stessa distanza da tre strade?
Il triangolo è una figura piana convessa formata da tre segmenti consecutivi che sono i suoi lati. Ogni coppia di lati ha un vertice in comune. In un triangolo ci sono tre angoli interni. Osservando gli oggetti di uso quotidiano riscontriamo diverse forme triangolari, i triangoli, infatti, si possono distinguere sia rispetto ai lati che rispetto agli angoli.
- Un triangolo con tre lati di lunghezza diversa, viene detto scaleno, dal latino scalenus che significa proprio disuguale.
- Un triangolo che ha due lati congruenti si definisce isoscele. Questo triangolo ha anche due angoli congruenti che sono entrambi adiacenti al terzo lato.
- Se i lati sono tutti congruenti tra loro e quindi anche gli angoli, il triangolo viene detto equilatero.
- il triangolo acutangolo i cui angoli sono tutti minori di un angolo retto;
- il triangolo rettangolo che ha un angolo retto;
- il triangolo ottusangolo che ha un angolo ottuso cioè maggiore di 90°.
In un triangolo da ciascun vertice si possono tracciare tre segmenti: l’altezza, la mediana e la bisettrice. In un triangolo quindi ce ne sono tre di ognuno, e ogni gruppo si interseca in un punto ben preciso. Questi punti sono detti punti notevoli di un triangolo e sono:
- ortocentro, punto d’incontro delle altezze;
- baricentro, punto di incontro delle mediane;
- incentro, punto di incontro delle bisettrici;
- circocentro, punto di incontro degli assi.
Proprietà del triangolo isoscele
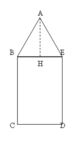
Nel triangolo isoscele i due lati congruenti vengono chiamati lati obliqui mentre il terzo lato è detto genericamente base. Quando si traccia l’altezza relativa alla base il triangolo isoscele viene diviso in due triangoli rettangoli perfettamente congruenti.L’altezza cade esattamente a metà della base, quindi, coincide anche con la mediana, poiché l’angolo al vertice è stato suddiviso in due parti uguali l’altezza è anche la bisettrice dell’angolo al vertice.
Abbiamo detto che gli angoli adiacenti alla base sono congruenti, nel caso in cui questi angoli misurino esattamente 45° l’uno vuol dire che l'angolo al vertice è un angolo retto, cioè misura 90°. Questo significa che il nostro triangolo isoscele è contemporaneamente anche rettangolo.
Se i due angoli alla base sono tutti e due di 30°, l’angolo al vertice risulta di 120 e la sua metà e 60. Questo vuol dire che quando tracciamo l’altezza i due triangoli rettangoli che si formano sono due triangoli rettangoli particolari, con gli angoli acuti di 30 e 60. Questi particolari triangoli rettangoli sono la metà di un triangolo equilatero.
Per ulteriori approfondimenti sugli angoli vedi anche qua
Figure isoperimetriche
Due poligoni diversi possono avere lo stesso perimetro anche se non hanno la stessa forma. Due figure che hanno lo stesso perimetro si dicono isoperimetriche. Non importa la forma che hanno questi poligoni, se misuriamo la lunghezza del loro perimetro, troviamo lo stesso risultato.Le due figure piane isoperimetriche possono avere anche un numero di dati diversi ad esempio: un quadrato e un triangolo, un rettangolo e un rombo, un cerchio e un quadrilatero qualsiasi oppure un cerchio e un triangolo.
Ricordiamo infine che la relazione di isoperimetria tra figure piane, gode della proprietà transitiva.
Se un poligono
[math]P_1[/math]
è isoperimetrico ad un poligono [math]P_2[/math]
e il poligono [math]P_2[/math]
a sua volta è isoperimetrico ad un poligono [math]P_3[/math]
, allora ne consegue che il poligono [math]P_1[/math]
è isoperimetrico al poligono [math]P_3[/math]
.Per ulteriori approfondimenti sui poligoni vedi anche qua
Problema svolto su triangoli isosceli isoperimetrici
Due triangoli isosceli sono isoperimetrici. Calcola il lato obliquo del secondo triangolo, sapendo che la base e il lato obliquo del primo misurano rispettivamente 20 e 25 cm, e che la base del secondo triangolo è la metà della base del primo triangolo.Svolgimento
Del primo triangolo conosciamo la misura della base e la misura del lato obliquo, possiamo calcolare subito il perimetro che è lo stesso anche per il secondo triangolo isoscele.
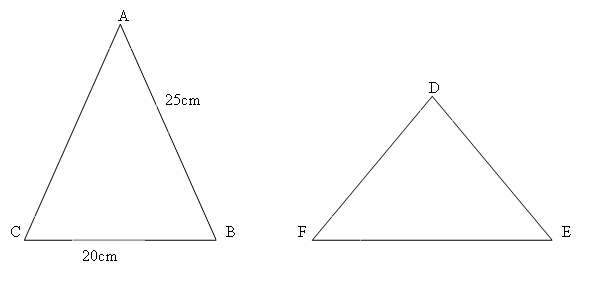
Facendo riferimento alla figura, il perimetro di entrambi è dato dalla somma dei lati:
[math]2p=AB+BC+AC=EF+FD+DE[/math]
Del primo sono note tutte le misure, quindi:
[math]2p=AB+BC+AC=25cm+20cm+25cm=70cm[/math]
Successivamente imponiamo che la somma dei lati del secondo triangolo sia uguale al perimetro calcolato.
[math]2\cdot l+b=70[/math]
La base del secondo triangolo è la metà di quella del primo quindi possiamo già scrivere che la sua misura è 10 cm:
[math]2\cdot l+10cm=70cm[/math]
Se dal perimetro sottraiamo il valore noto della base otteniamo che la somma dei due lati è uguale a 60 cm, dividendo per due scopriamo quanto misura il lato obliquo del secondo triangolo:
[math]60 cm =2\cdot l[/math]
[math]l=60 cm : 2=30cm[/math]
Il lato obliquo del secondo triangolo misura 30 cm.
per ulteriori approfondimenti sui triangoli isoperimetrici vedi anche qua
