Testo del problema
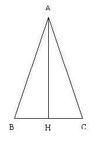
In un triangolo isoscele l'altezza è
[math]4/5[/math]
del lato e il perimetro misura [math]96cm[/math]
. Trovare l'area del triangolo. Soluzione
Detti
[math]h[/math]
l'altezza, [math]l[/math]
il lato e [math]2p[/math]
il perimetro, si ha: [math]h=\frac{4}{5}l[/math]
e [math]2p=96[/math]
. Per il Teorema di Pitagora si ha che [math]\frac{b}{2}[/math]
(ove [math]b[/math]
è la base del triangolo) è: [math]\frac{b}{2}=\sqrt{l^2 - h^2}=\sqrt{l^2 - \frac{16}{25}l^2}=\sqrt{\frac{9}{25}l^2}=\frac{3}{5}l[/math]
. Quindi, [math]b=\frac{6}{5}l[/math]
. Abbiamo il perimetro del triangolo, quindi la somma di tutti i lati (ricordiamoci che il triangolo è isoscele) deve dare quel valore Dunque: [math]2p=l+l+b[/math]
ovvero [math]2l+b=2l+\frac{6}{5}l=\frac{16}{5}l=96 => l=30[/math]
. Essendo [math]l=30[/math]
si ha dalle precedenti relazioni [math]b=36[/math]
e [math]h=24[/math]
, per cui, detta [math]A[/math]
l'area, si ha: [math]A=\frac{b\cdoth}{2}=\frac{36\cdot24}{2}=432[/math]
. FINE