Area e perimetro di figure composte
In questo tipo di problemi bisogna calcolare perimetro ed area di figure formate da più poligoni regolari posizionati uno accanto all'altro. Il più delle volte si tratta di figure semplici come ad esempio in questo caso solo triangoli, oppure figure con più lati; per la risoluzione è necessario individuare bene le caratteristiche dei poligoni presenti e sfruttarne tutte le proprietà.Per la risoluzione di questo problema di geometria dobbiamo ricordare le proprietà del triangolo isoscele e quelle del triangolo equilatero.
Testo del problema è strategia di soluzione
Il pentagono di vertici ABCDE è formato dal triangolo isoscele ABD e da due triangoli equilateri e congruenti DCB e ADE, posizionati sui lati obliqui del triangolo isoscele centrale. Sapendo che la base e l’altezza del triangolo isoscele sono una i tre mezzi dell’altra e che la loro somma è 360 cm, calcolare il perimetro e l’area del pentagono.
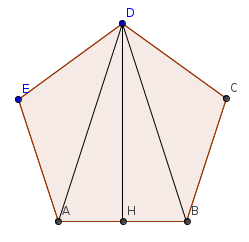
Il pentagono formato dalla composizione di questi tre triangoli non è un pentagono regolare perché uno dei lati non è congruente agli altri quattro. Il perimetro di questa figura è dato dalla somma di quattro lati congruenti che appartengono ai due triangoli equilateri più la base del triangolo isoscele, tutti da determinare.
L’area di questa figura piana composta è data dalla somma dell’area del triangolo isoscele e di quella dei due triangoli equilateri. Vediamo la procedura da seguire per determinare le misure incognite.
Indicazioni per lo svolgimento e richiami alle proprietà dei triangoli
Del triangolo isoscele è nota la somma delle misure di base ed altezza e la relazione che intercorre tra esse. È detto in particolare che il rapporto tra base e altezza è di tre a due, questo significa che la base è maggiore dell'altezza di una volta e mezza. La frazione che esprime il rapporto tra le misure di questi due lati rappresenta infatti il numero decimale 1,5.Con queste due informazioni possiamo scrivere una proporzione e poi applicando la proprietà del comporre calcoliamo la misura della base e dell’altezza.
Per calcolare la misura del lato obliquo, applichiamo il teorema di Pitagora. In un triangolo isoscele sappiamo che l’altezza relativa alla base è anche mediana relativa a questo lato e bisettrice dell'angolo al vertice, pertanto essa divide il triangolo isoscele in due triangoli rettangoli congruenti. L’ipotenusa di ciascuno di questi due triangoli è proprio il lato obliquo mentre i due cateti sono rappresentati dall’altezza del triangolo isoscele e metà della base.
Una volta calcolato il lato obliquo del triangolo isoscele sappiamo anche il lato del triangolo equilatero. L’ultima dimensione da determinare è l'altezza del triangolo equilatero per poterne calcolare l'area.
A questo proposito ricordiamo che in un triangolo equilatero, che è anche equiangolo esiste una relazione tra altezza e lato obliquo. In un triangolo equilatero quando tracciamo l’altezza, questa lo divide in due triangoli rettangoli con angoli acuti di 30° e 60°. In ciascuno di questi triangoli rettangoli il cateto minore è la metà del lato obliquo mentre l'altezza è uguale alla metà del lato obliquo moltiplicato per la radice di tre.
Ora che abbiamo sviluppato tutto il ragionamento da seguire non ci resta che passare allo svolgimento pratico e quindi ai calcoli da effettuare.
Perimetro della figura composta
Calcoliamo la misura di base ed altezza del triangolo isoscele impostando la proporzione E applicando la proprietà del comporre.
Per differenza ora calcoliamo la misura dell’altezza h:
N.B. Allo stesso modo potevamo procedere per determinare h con la proporzione e poi b.
Applichiamo ora il teorema di Pitagora al triangolo rettangolo AHD. L’ipotenusa di questo triangolo è il lato obliquo del triangolo isoscele pertanto la sua misura È data dalla radice quadrata della somma dei quadrati dei due cateti che sono l’altezza e la metà della base.
Nota la misura del lato obliquo, che è anche il lato del triangolo equilatero, possiamo determinare la misura del perimetro:
Area della figura composta
Del triangolo isoscele è possibile calcolare l’area, essendo note le misure di b e di h. Ricordiamo che l’area è pari al semiprodotto di base e altezza:
Per poter calcolare l’area del triangolo equilatero dobbiamo prima determinarne l’altezza. Per le proprietà del triangolo equilatero, si può esprimere la misura dell'altezza in funzione del lato:
Inseriamo i valori numerici
La misura dell’altezza del triangolo equilatero è un numero irrazionale. Utilizzando il simbolo circa uguale

Visto che i due triangoli equilateri sono congruenti, essi sono anche equivalenti perciò hanno la stessa area. Non effettuiamo perciò la divisione per due, in questo modo abbiamo l'area totale dei due triangoli equilateri.
Sommiamo all’area del triangolo isoscele per ottenere l'area del pentagono:
Per ulteriori approfondimenti sull’area del Pentagono vedi anche qui



