Dato un rettangolo, con la base e l'altezza di misura rispettivamente
[math]b[/math]
ed [math]h[/math]
, individuare il triangolo rettangolo circoscritto ad esso (con il vertice dell'angolo retto coin-cidente con un vertice del rettangolo) di area minima; trovare poi la relazione fra [math]b[/math]
ed [math]h[/math]
in modo che tale triangolo sia la metà di uno equilatero. 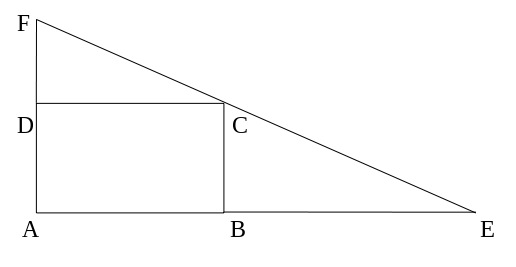
I segmenti
[math]AB[/math]
e [math]CD[/math]
misurano [math]b[/math]
, i segmenti [math]AD[/math]
e [math]BC[/math]
misurano [math]h[/math]
; indichiamo con [math]x[/math]
la misura di [math]BE[/math]
(deve essere [math]x>0[/math]
). Dalla similitudine dei triangoli [math]BCE[/math]
e [math]CDF[/math]
risulta che [math]DF : BC = CD : BE[/math]
, da cui, passando alle misure, si ha ( overline{DF} : h = b : x ), da cui ( overline{DF} = bh/x ). I segmenti [math]AE[/math]
ed [math]AF[/math]
misurano quindi rispettivamente [math]b+x[/math]
, (h + (bh/x)) e l'area del triangolo [math]AEF[/math]
(che è quella da minimizzare) risulta [ y = (b+x) cdot Big(h + frac{bh}{x} Big) ] da cui [ ag{*} y = hx + frac{b^2h}{x}+2bh ext{, con } x > 0 ]. La derivata di tale funzione è
[math] dot{y} = h - frac{b^2h}{x^2} = frac{hx^2-b^2h}{x^2} [/math]
che esiste per ogni [math] x != 0 [/math]
, si annulla per [math] x = +- b [/math]
(interessa solo [math]x = b[/math]
), è negativa se [math]-b , è positiva se
[math]x b[/math]
, la funzione [math]y[/math]
ha quindi, nell'intervallo [math](0; +oo)[/math]
minimo relativo ed assoluto in [math]x = b[/math]
. Il triangolo di area minima cercato ha quindi i cateti
[math]AE[/math]
ed [math]AF[/math]
di misura rispettivamente [math]2b[/math]
e [math]2h[/math]
. Per minimizzare la funzione
[math]y[/math]
si poteva anche evitare di ricorrere al calcolo differenziale utilizzando il "metodo delle proprietà note1". Osservando [math]y[/math]
nella (*) si nota che, essendo il terzo addendo costante, ci si può limitare a minimizzare la somma dei primi due addendi; questi sono positivi con prodotto costante (uguale a [math]b^2h^2[/math]
), pertanto, in base a una delle "proprietà note", la loro somma è minima quando essi sono uguali, il che accade se [math]x = b[/math]
. Affinchè un triangolo rettangolo sia la metà di uno equilatero, occorre e basta che uno dei suoi angoli acuti abbia ampiezza
[math]60°[/math]
; nel triangolo in questione si deve quindi imporre che tale ampiezza sia quella dell'angolo in [math]E[/math]
o dell'angolo in [math]F[/math]
. Deve quindi risultare:
(overline{AF} = overline{AE} cdot an 60° ) ossia
[math]2b = 2h cdot \sqrt{3}[/math]
da cui [math]b = h \sqrt{3}[/math]
oppure
(overline{AE} = overline{AF} cdot an 60° ) ossia
[math]2h = 2b cdot \sqrt{3}[/math]
da cui [math]h = b \sqrt{3}[/math]
. Note: 1. Cfr. ad esempio M. Dedò, Matematiche elementari , vol. I, parte III, cap. I, Liguori Editore (1962)