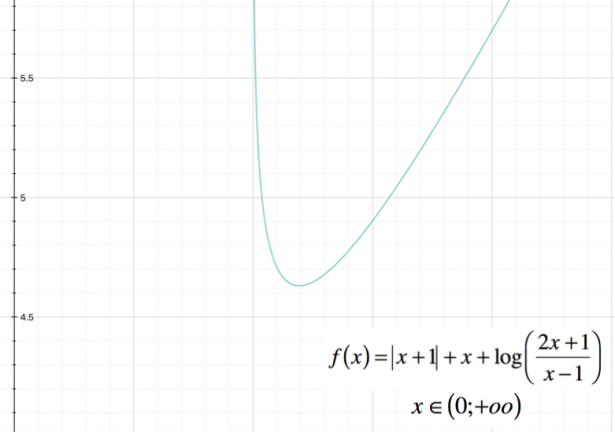Cominciamo lo studio di funzione determinando il dominio della funzione; poiché è presente una funzione logaritmica, dobbiamo imporre che il suo argomento sia maggiore di zero:
[math]frac(2x+1)(x-1) > 0[/math]
[math]2x +1 > 0[/math]
[math]x-1 > 0[/math]
Dallo studio del segno si ottengono i seguenti intervalli:
[math] x 1 [/math]
Quindi abbiamo:
[math] D = (-oo ; -1/2) uu (1 ; +oo) [/math]
.
In questo caso, quindi, la funzione non presenta nessuna intersezione con gli assi, in quanto tutti i punti possibili sono comunque esclusi dal dominio.
Verifichiamo se la funzione è pari o dispari:
[math] f(-x) = |-x+1| - x + \\log(frac(-2x+1)(-x-1)) [/math]
La funzione quindi non è ne pari ne dispari.
Passiamo alla ricerca degli asintoti; dobbiamo determinare i limiti della funzione, cominciamo dal limite a
[math]+oo[/math]
:
[math] lim_(x \to +oo) |x+1| + x + \\log(frac(2x+1)(x-1)) [/math]
In questo intorno, possiamo assumere che
[math] |x+1| = x + 1[/math]
, quindi:
[math] lim_(x \to +oo) |x+1| + x + \\log(frac(2x+1)(x-1)) = [/math]
[math]lim_(x \to +oo) x+1 + x + \\log(frac(2x+1)(x-1)) =[/math]
[math]lim_(x \to +oo) 2x + 1 + \\log(frac(2x+1)(x-1)) = +oo [/math]
La funzione, quindi, non presenta asintoti orizzontali destri.
Studiamo il comportamento a
[math]- oo[/math]
; in questo caso si avrà
[math] |x+1| = - x - 1[/math]
:
[math] lim_(x \to -oo) |x+1| + x + \\log(frac(2x+1)(x-1)) = [/math]
[math]lim_(x \to -oo) -x-1 + x + \\log(frac(2x+1)(x-1)) =[/math]
[math] lim_(x \to -oo) - 1 + \\log(frac(2x+1)(x-1)) = \\log(2) - 1 [/math]
Di conseguenza, la retta di equazione
[math]y = \\log(2) - 1[/math]
è un asintoto orizzontale sinistro per la funzione.
Poiché la funzione presenta solo un asintoto orizzontale sinistro, "a destra" potrebbe essere presente un asintoto obliquo; in tal caso, il coefficiente angolare di tale asintoto è dato da un valore finito di tale limite:
[math] m = lim_(x \to +oo) frac(f(x))(x) = lim_(x \to +oo) 2 + 1/x + frac(\\log(frac(2x+1)(x-1)))(x) = 2[/math]
Avendo ottenuto un valore finito per
[math]m[/math]
, cerchiamo un eventuale
[math]q[/math]
:
[math] q = lim_(x \to +oo) [f(x) - mx] = [/math]
[math]lim_(x \to +oo) 2x + 1 + \\log(frac(2x+1)(x-1)) - 2x = 1 + \\log(2) [/math]
Possiamo concludere, quindi, che la retta
[math] y = 2x + 1 + \\log(2)[/math]
è un asintoto obliquo destro per la funzione.
Vediamo ora cosa accade quando la funzione si avvicina ai punti che sono esclusi dal dominio; in particolare, risolviamo i seguenti limiti:
[math] lim_(x \to -1/2 ^-) |x+1| + x + \\log(frac(2x+1)(x-1)) = [/math]
[math]lim_(x \to -1/2 ^-) x+1 + x + \\log(frac(2x+1)(x-1)) =[/math]
[math] lim_(x \to -1/2 ^-) 2x + 1 + \\log(frac(2x+1)(x-1)) = -oo [/math]
La retta
[math] x = -1/2[/math]
è quindi asintoto verticale per la funzione.
[math] lim_(x \to 1^+) |x+1| + x + \\log(frac(2x+1)(x-1)) = [/math]
[math]lim_(x \to 1^+) x+1 + x + \\log(frac(2x+1)(x-1)) =[/math]
[math]lim_(x \to 1^+) 2x + 1 + \\log(frac(2x+1)(x-1)) = +oo [/math]
Anche la retta
[math] x = 1[/math]
è asintoto verticale per la funzione.
Cerchiamo eventuali punti di massimo o minimo studiando la derivata prima; distendiamo i casi
[math]x > -1[/math]
e
[math]x ; nel primo caso si ha:
[math] f'(x) = 2 + frac(x-1)(2x+1) \cdot frac(2(x-1) - 2x - 1)((x-1)^2) = [/math]
[math]2 - frac(3)((2x+1)(x-1)) = [/math]
[math] frac(4x^2 - 2x - 5)( (2x+1)(x-1) ) [/math]
Troviamo i punti in cui la deriva prima si annulla:
[math] f'(x) = 0 \to frac(4x^2 - 2x - 5)( (2x+1)(x-1) ) = 0 [/math]
[math] 4x^2 - 2x - 5 = 0 \to x = frac(1+\sqrt{21})(4) vee x = frac(1-\sqrt{21})(4) [/math]
Studiamo il segno della derivata prima:
[math] f'(x) > 0 \to frac(4x^2 - 2x - 5)( (2x+1)(x-1) ) > 0 [/math]
[math] 4x^2 - 2x - 5 > 0 [/math]
[math] (2x+1)(x-1) > 0 [/math]
Dallo studio del segno e tenendo conto che siamo nel caso in cui
[math]x > -1 [/math]
otteniamo i seguenti intervalli:
[math] ( - 1 , frac(1-\sqrt{21})(4) ) uu ( frac(1+\sqrt{21})(4) ; +oo ) [/math]
; la funzione, quindi, è crescente in tali intervalli.
Notiamo, quindi, che il punto individuato da
[math] x = frac(1+\sqrt{21})(4) [/math]
è un punto di minimo relativo per la funzione, mentre il punto individuato da
[math] x = frac(1-\sqrt{21})(4) [/math]
è un punto di massimo relativo per la funzione.
Passiamo ora al caso
[math] x :
[math] f'(x) = frac(x-1)(2x+1) \cdot frac(2(x-1) - 2x - 1)((x-1)^2) = frac(3)((2x+1)(x-1)) [/math]
Troviamo i punti in cui la deriva prima si annulla:
[math] f'(x) = 0 \to frac(3)((2x+1)(x-1)) = 0 [/math]
In questo caso la derivata prima non si annulla in nessun punto; dallo studio del segno si trova il seguente intervallo:
[math] (-1/2 , 1) [/math]
Quindi, nell'intervallo che stiamo considerando, la derivata sarà sempre negativa, di conseguenza la funzione sarà decrescente nell'intervallo
[math] x .
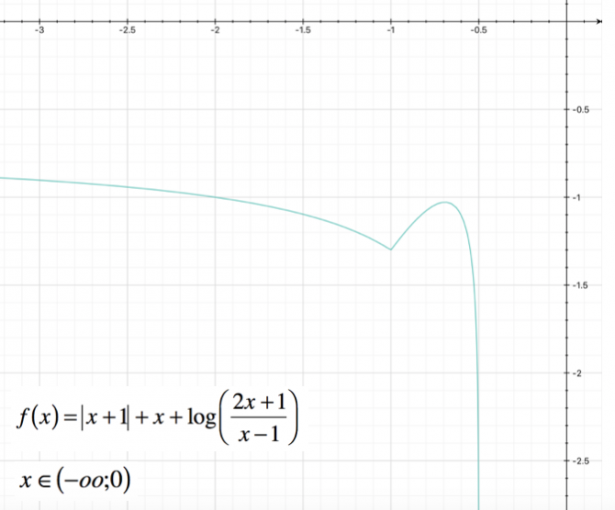
In questo caso, il calcolo della derivata seconda si rivela troppo complesso; possiamo comunque tracciare il grafico approssimativo della funzione:
Nell'intervallo
[math] (-oo ; 0) [/math]
si avrà un grafico di questo tipo:
Mentre nell'intervallo
[math] ( 0 ; +oo ) [/math]
si avrà un grafico di questo tipo:
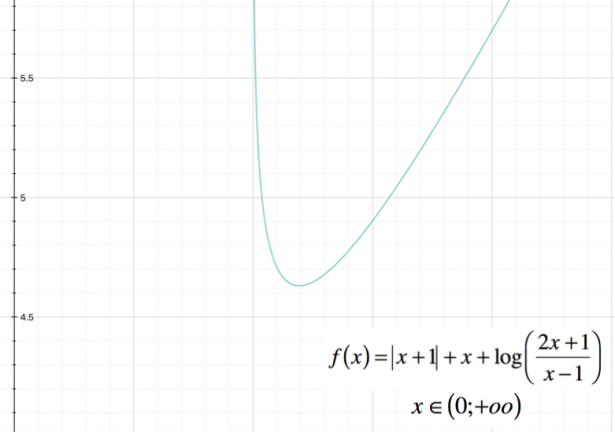
Potrebbe interessarti anche