La funzione può essere scritta anche nel modo seguente:
[math] f(x) = frac(1)( e^{x^2} (x + 2)) [/math]
Nel caso di funzioni fratte, dobbiamo escludere dal dominio i valori che annullano il denominatore; in questo caso:
[math] e^{x^2} (x + 2) = 0 \to x + 2 = 0 \to x = - 2[/math]
Quindi il dominio sarà l'insieme dei numeri reali eccetto il numero -2:
[math] D = R - {-2} [/math]
.
Determiniamo ora i punti di intersezione con gli assi:
[math] f(x) _|_ (x = 0) [/math]
[math] f(0) = frac(1)( e^{0^2} (0 + 2)) =1/2 [/math]
Il punto individuato è
[math] ( 0 ; 1/2 ) [/math]
.
Quindi la funzione ha un punto di intersezione con l'asse y.
[math] f(x) _|_ y = 0[/math]
[math] f(x) = 0 \to frac(1)( e^{x^2} (x + 2)) = 0 [/math]
Dato che l'uguaglianza non può essere verificata per nessun valore di x, concludiamo che la funzione non presenta punti di intersezione con l'asse x.
Verifichiamo se la funzione è pari o dispari:
[math] f(-x) = frac(1)( e^{(-x)^2} (-x + 2)) = frac(1)( e^{x^2} (-x + 2)) [/math]
La funzione quindi non è ne pari ne dispari.
Cerchiamo gli intervalli in cui la funzione è positiva:
[math] f(x) > 0 \to frac(1)( e^{x^2} (x + 2)) > 0 \to e^{x^2} (x + 2) > 0 [/math]
[math] x + 2 > 0 \to x > - 2 [/math]
La funzione è positiva nel seguente intervallo:
[math] ( -2 ; +oo ) [/math]
.
Passiamo ora alla ricerca degli asintoti; dobbiamo determinare i limiti della funzione, cominciamo in questo caso dal limite a
[math]oo[/math]
:
[math] lim_(x \to oo) frac(1)( e^{x^2} (x + 2)) [/math]
Non vi sono in questo limite forme di indecisione, e il valore può essere calcolato facilmente:
[math] lim_(x \to oo) frac(1)( e^{x^2} (x + 2)) = 0 [/math]
La funzione, quindi, ha come asintoto orizzontale (destro e sinistro) la retta di equazione
[math]y = 0[/math]
.
Poiché la funzione non è definita in
[math]x = -2[/math]
, verifichiamo se in tale punto è presente un asintoto verticale calcolando i seguenti limiti:
[math] lim_(x \to -2^+) frac(1)( e^{x^2} (x + 2)) , lim_(x \to -2^-) frac(1)( e^{x^2} (x + 2)) [/math]
I limiti destro e sinistro assumono i seguenti valori:
[math] lim_(x \to -2^+) frac(1)( e^{x^2} (x + 2)) = + oo [/math]
[math] lim_(x \to -2^-) frac(1)( e^{x^2} (x + 2)) = - oo [/math]
Quindi, la retta
[math] x = - 2[/math]
è asintoto verticale (destro e sinistro) per la funzione.
Cerchiamo ora eventuali punti di massimo o minimo; calcoliamo la derivata prima della funzione:
[math] f'(x) = - frac(e^{x^2} \cdot 2x(x + 2) + e^{x^2} )( e^{2x^2}(x+2)^2 ) = - frac( 2x^2 + 4x + 1)( e^{x^2}(x+2)^2 ) [/math]
Troviamo i punti in cui la derivata prima si annulla:
[math] f'(x) = 0 \to - frac( 2x^2 + 4x + 1)( e^{x^2}(x+2)^2 ) = 0 [/math]
[math] 2x^2 + 4x + 1 = 0 \to x = -1 + frac(\sqrt2){2} V x = -1 - frac(\sqrt2){2} [/math]
Studiamo il segno della derivata prima:
[math] f'(x) > 0 \to - frac( 2x^2 + 4x + 1)( e^{x^2}(x+2)^2 ) > 0 [/math]
[math] - (2x^2 + 4x + 1) > 0 [/math]
[math] e^{x^2} > 0 [/math]
[math] (x+2)^2 > 0 [/math]
Dallo studio del segno si ottiene l'intervallo:
[math] ( -1 - frac(\sqrt2){2} , -1 + frac(\sqrt2){2} ) [/math]
; la funzione, quindi, è crescente in tale intervallo.
Notiamo, quindi, che il punto individuato da
[math] x = -1 - frac(\sqrt2){2} [/math]
è un punto di minimo relativo per la funzione, mentre il punto individuato da
[math] x = -1 + frac(\sqrt2){2} [/math]
è un punto di massimo relativo per la funzione
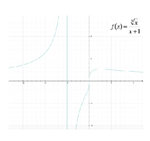
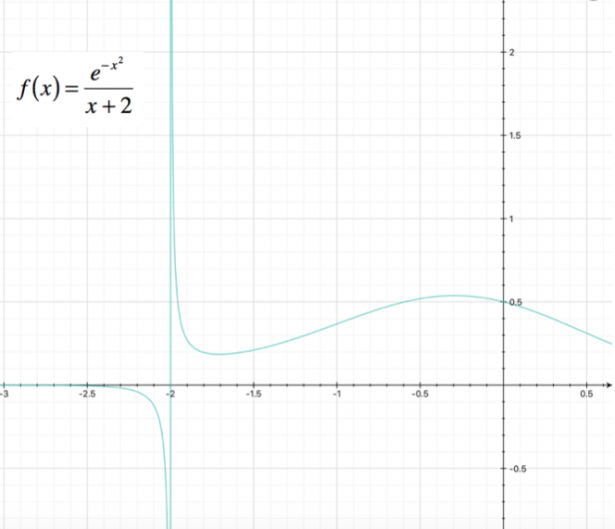
In questo caso, lo studio della derivata seconda si rileva troppo complesso; possiamo comunque procedere rappresentando il grafico approssimativo della funzione:
Potrebbe interessarti anche