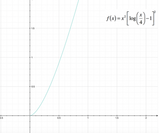
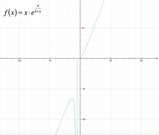
La funzione si presenta come il prodotto tra due funzioni, di cui una lineare e l'altra esponenziale; in questo caso, quindi, il dominio della funzione è l'insieme dei
numeri reali:
[math] D = R [/math]
.
Determiniamo ora i punti di intersezione con gli assi:
[math] f(x) _|_ (x = 0) [/math]
[math] f(0) = (0^2 + 0) e^{0+1} = 0 [/math]
Il punto individuato è
[math] ( 0 ; 0 ) [/math]
.
[math] f(x) _|_ (y = 0)[/math]
[math] f(x) = 0 \to (x^2 + x) e^{x+1} = 0 [/math]
[math] x^2 + x = 0 \to x(x+1) = 0 \to x = 0 V x = -1[/math]
In questo caso abbiamo due punti, di cui uno già individuato in precedenza (
[math] ( 0 ; 0 ) [/math]
), e l'altro
[math] ( -1 ; 0 ) [/math]
.
Verifichiamo se la funzione è pari o dispari:
[math] f(-x) = ((-x)^2 - x) e^{-x+1} [/math]
La funzione quindi non è ne pari ne dispari.
Cerchiamo gli intervalli in cui la funzione è positiva:
[math] f(x) > 0 \to (x^2 + x) e^{x+1} > 0 \to x^2 + x > 0 [/math]
Poiché l'esponenziale è sempre positivo, la funzione è positiva negli intervalli:
[math] ( -oo ; -1 ) uu ( 0 ; +oo )[/math]
.
Passiamo ora alla ricerca degli asintoti; dobbiamo determinare i limiti della funzione, cominciamo in questo caso dal limite a
[math]+oo[/math]
:
[math] lim_(x \to +oo) (x^2 + x) e^{x+1} [/math]
Non vi sono in questo limite forme di indecisione, e il valore può essere calcolato facilmente:
[math] lim_(x \to +oo) (x^2 + x) e^{x+1} = +oo [/math]
Calcoliamo ora il limite a
[math]-oo[/math]
:
[math] lim_(x \to -oo) (x^2 + x) e^{x+1} [/math]
In questo caso abbiamo una forma di indecisione del tipo
[math] oo \cdot 0 [/math]
; per risolverla, possiamo portare l'esponenziale al denominatore:
[math] lim_(x \to -oo) (x^2 + x) e^{x+1} = lim_(x \to -oo) frac( x^2 + x)(e^{-x-1}) [/math]
Ora sia numeratore che denominatore tendono a
[math]+oo[/math]
, ma il denominatore è un
infinito di ordine maggiore del numeratore, quindi tenderà ad infinito più velocemente; il valore del limite è quindi:
[math] lim_(x \to -oo) frac( x^2 + x)(e^{-x-1}) = 0 [/math]
La retta
[math] y = 0[/math]
è quindi un asintoto orizzontale sinistro per la funzione.
Poiché non ci sono asintoti orizzontali per
[math]x \to +oo[/math]
, occorre verificare se la funzione presenta asintoti obliqui per
[math]x \to +oo[/math]
:
[math] m = lim_(x \to oo) frac(f(x))(x) = lim_(x \to oo) frac( x + 1)(e^{x+1}) = +oo [/math]
Abbiamo trovato un valore infinito del limite, di conseguenza non sono presenti asintoti obliqui.
Cerchiamo ora eventuali punti di massimo o minimo; calcoliamo la derivata prima della funzione:
[math] f'(x) = (2x + 1) e^{x+1} + (x^2 + x) e^{x+1} = [/math]
[math] e^{x+1} (2x + 1 + x^2 + x) = [/math]
[math] e^{x+1} (x^2 + 3x + 1) [/math]
Troviamo i punti in cui la deriva prima si annulla:
[math] f'(x) = 0 \to e^{x+1} (x^2 + 3x + 1) = 0 [/math]
[math] x^2 + 3x + 1 = 0 \to x = frac(-3 + \sqrt5){2} uu x = frac(-3 - \sqrt5){2} [/math]
Studiamo il segno della derivata prima:
[math] f'(x) > 0 \to e^{x+1} (x^2 + 3x + 1) > 0 [/math]
[math] e^{x+1} > 0 [/math]
[math] x^2 + 3x + 1 > 0 [/math]
Dallo studio del segno si ottengono i seguenti intervallo:
[math] ( - oo , frac(-3 - \sqrt5){2} ) uu ( frac(-3 + \sqrt5){2} ; +oo) [/math]
;
la funzione, quindi, è crescente in tali intervalli.
Notiamo, quindi, che il punto individuato da
[math] x = frac(-3 + \sqrt5){2} [/math]
è un
punto di minimo relativo per la funzione, mentre il punto individuato da
[math] x = frac(-3 - \sqrt5){2} [/math]
è un punto di massimo relativo per la funzione.
Calcoliamo ora la derivata seconda della funzione:
[math] f''(x) = e^{x+1} (x^2 + 3x + 1) + e^{x+1} (2x + 3) = [/math]
[math]e^{x+1} (x^2 + 3x + 1 + 2x + 3) = [/math]
[math] e^{x+1} (x^2 + 5x + 4) [/math]
Troviamo i valori di x che annullano la derivata seconda:
[math] f''(x) = 0 \to e^{x+1} (x^2 + 5x + 4) = 0 [/math]
[math] x^2 + 5x + 4 = 0 \to x = frac(-5 \pm \sqrt{25 - 16})(2) = frac(-5 \pm 3)(2) [/math]
[math] x = -1 uu x = -4 [/math]
Studiamo il segno della derivata seconda:
[math] f''(x) > 0 \to e^{x+1} (x^2 + 5x + 4) > 0[/math]
[math] e^{x+1} > 0 [/math]
[math] x^2 + 5x + 4 > 0 [/math]
Dallo studio del segno si trova che
[math] x -1 [/math]
; di conseguenza, la funzione sarà concava verso l'alto per x in tale intervallo, e sarà rivolta verso il basso per
[math] -4 .
I punti individuati da
[math] x = -4[/math]
e
[math] x = -1[/math]
sono quindi punti di flesso.
Possiamo tracciare il grafico della funzione:
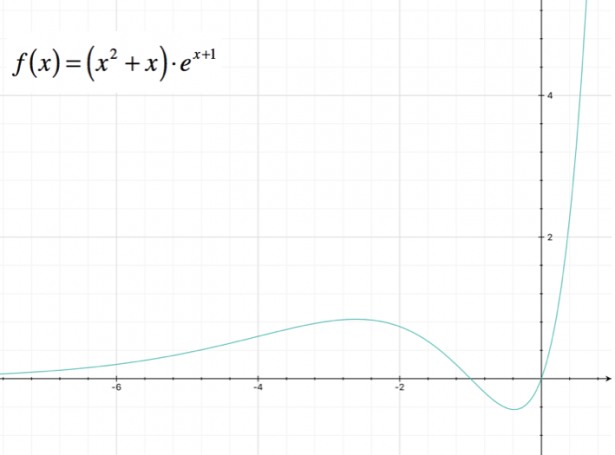
Potrebbe interessarti anche