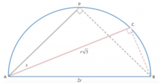
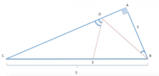
Dimostrare che:
[math] PA = PB + PC [/math]

Svolgimento
Essendo[math]ABC[/math]
un triangolo equilatero, sappiamo che:
[math] hatA = hatB = hatC = 60° [/math]
Inoltre sappiamo che:
[math] hat{PAB} = hat{PCB} [/math]
Perché angoli che insistono sulla stessa corda.
Chiamiamo questi angoli con
[math]alpha[/math]
; possiamo quindi affermare che:
[math]hat{ACP} = 60° + alpha [/math]
[math]hat{CAP} = 60° - alpha [/math]
Possiamo ora sfruttare il teorema della corda, secondo il quale, in una circonferenza, ogni corda è uguale al prodotto del diametro per il seno dell'angolo ad essa opposto.
[math] hat{AP} = 2r \cdot \\sin (60° + alpha) [/math]
[math] hat{PB} = 2r \cdot \\sin (alpha) [/math]
[math] hat{CP} = 2r \cdot \\sin (60° - alpha) [/math]
Per dimostrare l'uguaglianza richiesta dal problema, impostiamo che
[math]PA = PB + PC [/math]
: dovremmo ottenete un'identità:
[math] 2r \cdot \\sin (60° + alpha) = 2r \cdot \\sin(alpha) + 2r \cdot \\sin (60° - alpha) [/math]
Possiamo semplificare
[math]2r[/math]
:
[math] \\sin (60° + alpha) = \\sin(alpha) + \\sin (60° - alpha) [/math]
Ora applichiamo le formule di addizione e di sottrazione del seno:
[math] \\sin (60°) \\cos(alpha) + \\cos(60°) \\sin(alpha) = \\sin(alpha) + \\sin (60°) \\cos(alpha) - \\cos(60°) \\sin(alpha) [/math]
[math] \\cos(60°) \\sin (alpha) = \\sin (alpha) - \\cos(60°) \\sin (alpha) [/math]
Sapendo che
[math] \\cos(60°) = 1/2 [/math]
:
[math] 1/2 \\sin (alpha) = \\sin (alpha) - 1/2 \\sin (alpha) [/math]
[math] frac(\\sin (alpha))(2) = \\sin(alpha) - frac(\\sin (alpha))(2) [/math]
[math] frac(\\sin (alpha))(2) = frac( 2\\sin(alpha) - \\sin(alpha) )(2) [/math]
[math] frac(\\sin (alpha))(2) = frac(\\sin (alpha))(2) [/math]
Abbiamo quindi verificato che
[math]PA = PB + PC [/math]
.