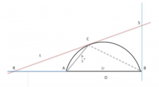
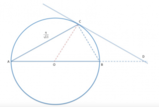
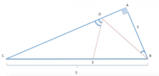
[math]AC = r \sqrt3 [/math]
una corda di una semicirconferenza di diametro [math]AB = 2r[/math]
. Determinare sull’arco [math]AC[/math]
un punto [math]P[/math]
tale che risulti[math]AP + PC = 2r[/math]

Svolgimento
Per prima cosa, poniamo l’angolo[math]\hat{PAC}[/math]
uguale a [math]x[/math]
.Dal teorema della corda, sappiamo che la corda
[math]PC[/math]
è uguale al prodotto del diametro per il seno del suo angolo opposto:[math]PC = 2r \sin x[/math]
Consideriamo il triangolo
[math]\hat{ACB}[/math]
, rettangolo poiché inscritto in una semicirconferenza. Possiamo trovare il valore del coseno dell’angolo [math]\hat{CAB}[/math]
sfruttando il primo teorema sui triangoli rettangoli:[math]\cos(\hat{CAB}) = \frac{AC}{AB} = \frac{r\sqrt3}{2r} = \frac{\sqrt3}{2} [/math]
Essendo l’angolo in questione un angolo acuto, possiamo affermare che esso ha ampiezza
[math]30°[/math]
.[math]\hat{CAB} = 30°[/math]
Di conseguenza, l’angolo
[math]\hat{PAB}[/math]
vale [math]x + 30°[/math]
.Considerando il triangolo
[math]\hat{PAB}[/math]
, anch’esso rettangolo, possiamo trovare la lunghezza del cateto [math]AP[/math]
:
[math]AP = AB \cos(\hat{PAB}) = 2r \cdot \cos(x + 30°)[/math]
Applichiamo le formule di addizione del coseno:
[math]AP = 2r \cdot \cos(x + 30°) = 2r \cdot (\cos x \cos(30°) - \sin \sin(30°)) = [/math]
[math]2r \cdot (\cos x \cdot \frac{\sqrt3}{2} - \sin \cdot \frac{1}{2} = r \sqrt3 \cos x - r \sin x [/math]
Avendo un’espressione di
[math]AP[/math]
e di [math]PC[/math]
in funzione di [math]x[/math]
, possiamo impostare l’uguaglianza:[math]AP + PC = 2r[/math]
[math] r \sqrt3 \cos x - r \sin x + 2r \sin x = 2r [/math]
[math] \sqrt3 \cos x + \sin x = 2 [/math]
Risolviamo con il metodo dell’angolo aggiunto:
[math] \tan(\frac{\pi}{3}) \cos x + \sin x = 2 [/math]
[math] \frac{\sin (\frac{\pi}{3}}{\cos(\frac{\pi}{3})} \cos x + \sin x = 2 [/math]
[math] \sin (\frac{\pi}{3}) \cos x + \cos(\frac{\pi}{3}) \sin x = 2\cos(\frac{\pi}{3}) [/math]
[math] \sin (\frac{\pi}{3}) \cos x + \cos(\frac{\pi}{3}) \sin x = 1 [/math]
Riconoscendo la formula di addizione del seno:
[math] \sin (\frac{\pi}{3} + x) = 1 [/math]
[math] \frac{\pi}{3} + x = \frac{\pi}{2} + k\pi [/math]
[math] x = \frac{\pi}{2} - \frac{\pi}{3} + k\pi = \frac{\pi}{6} + k\pi [/math]
Concludiamo che l’angolo
[math]x[/math]
deve essere uguale a [math] \frac{\pi}{6}[/math]
.