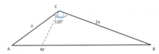
Nel triangolo
[math]ABC[/math]
rettangolo in
[math]A[/math]
si sa che
[math]AB = 3[/math]
e
[math]BC = 5[/math]
. Siano
[math]D[/math]
un punto di
[math]AC[/math]
tale che
[math]tg(hat{ABD}) = 2/3 [/math]
ed
[math]E[/math]
il punto di
[math]BC[/math]
tale che risulti
[math] hat{EDC} = 2 hat{ABD}[/math]
.
Determinare perimetro e area del triangolo
[math]DEC[/math]
.

Svolgimento
Consideriamo il
triangolo rettangolo [math]ABD[/math]
; possiamo applicare il secondo teorema sui triangoli rettangoli per trovare il cateto
[math]AD[/math]
, conoscendo la tangente dell'angolo
[math]hat{ABD}[/math]
:
[math]AD = AB \cdot tg(hat{ABD}) = 3 \cdot 2/3 = 2 [/math]
Ora, consideriamo il triangolo rettangolo
[math]ABC[/math]
e troviamo il valore del lato
[math]AC[/math]
con il teorema di
Pitagora:
[math]AC = \sqrt{BC^2 - AB^2} = \sqrt(5^2 - 3^2) = \sqrt(25 - 9) = \sqrt(16) = 4 [/math]
Troviamo ora, per differenza, il lato
[math]DC[/math]
del triangolo
[math]DEC[/math]
:
[math] DC = AC - AD = 4 - 2 = 2 [/math]
Ricaviamo ora il seno e il coseno dell'angolo
[math]hat{ABD}[/math]
dal valore della sua tangente:
[math] \\sin (hat{ABD}) = frac(tg(hat{ABD}))(\sqrt{1 + tg^2 (hat{ABD})}) = [/math]
[math] frac(2/3)(\sqrt{1 + (2/3)^2}) = frac(2/3)(\sqrt(1 + 4/9)) = frac(2/3)(\sqrt((13)/9)) = [/math]
[math] 2/3 \cdot frac(3)(\sqrt{13}) = frac(2)(\sqrt{13}) [/math]
[math] \\cos(hat{ABD}) =\sqrt{1 - \\sin ^2 (hat{ABD})} = \sqrt(1 - (frac(2)(\sqrt(13)))^2) = [/math]
[math] \sqrt{1 - frac(4)(13)} = \sqrt(frac(9)(13)) = frac(3)(\sqrt(13)) [/math]
Sapendo che l'angolo
[math]hat{EDC}[/math]
è doppio dell'angolo
[math]hat{ABD}[/math]
, possiamo scrivere che:
[math] \\sin (hat{EDC}) = \\sin(2 hat{ABD}) [/math]
Risolviamo con le formule di duplicazione:
[math] \\sin (hat{EDC}) = \\sin(2 hat{ABD}) = 2 \\sin (hat{ABD})\\cos(hat{ABD}) = [/math]
[math] 2 \cdot frac(2)(\sqrt{13}) \cdot frac(3)(\sqrt{13}) = frac(12){13} [/math]
[math] \\cos(hat{EDC}) =\sqrt{1 - \\sin ^2 (hat{EDC})} = \sqrt(1 - (frac(12)(13))^2) = [/math]
[math] \sqrt{1 - frac(144)(169)} = \sqrt(frac(25)(169)) = frac(5)(\sqrt(13)) [/math]
Ora, considerando il triangolo rettangolo
[math]ABC[/math]
, possiamo ricavare tramite il primo teorema sui triangolo rettangoli il seno dell'angolo
[math]hat{DCE}[/math]
:
[math] \\sin (hat{DCE}) = frac(AB)(BC) = 3/5 [/math]
[math] \\cos(hat{DCE}) =\sqrt{1 - \\sin ^2 (hat{DCE})} = \sqrt(1 - (frac(3)(5))^2) = [/math]
[math] \sqrt{1 - frac(9)(25)} = \sqrt(frac(16)(25)) = frac(4)(5) [/math]
In questo modo possiamo ricavare anche il seno dell'angolo
[math]hat{DEC}[/math]
, sapendo che
[math] hat{DEC} = 180° - (hat{EDC} + hat{DCE})[/math]
[math] \\sin (hat{DEC}) = \\sin(180° - (hat{EDC} + hat{DCE}))[/math]
Considerando gli angoli associati, possiamo scrivere direttamente che:
[math] \\sin (hat{DEC}) = \\sin (hat{EDC} + hat{DCE})[/math]
Applichiamo la formula di addizione del seno:
[math] \\sin (hat{EDC} + hat{DCE}) = \\sin (hat{EDC}) \\cos(hat{DCE}) + \\cos(hat{EDC}) \\sin (hat{DCE}) = [/math]
[math] frac(12)(13) \cdot 4/5 + frac(5)(13) \cdot 3/5 = frac(48)(65) + frac(3)(13) = frac(63)(65) [/math]
Applichiamo ora il teorema dei seni al triangolo
[math]DEC[/math]
per trovare il lato
[math]DE[/math]
:
[math] frac(DC)(\\sin (hat{DEC})) = frac(DE)(\\sin (hat{DCE})) [/math]
[math] DE = frac(DC \cdot \\sin (hat{DCE}))(\\sin(hat{DEC})) = frac(2 \cdot 3/5)(frac(63)(65)) = [/math]
[math] 6/5 \cdot frac(63)(65) = frac(26)(21) [/math]
Possiamo quindi già determinare l'area del triangolo
[math]DEC[/math]
:
[math]A_(DEC) = 1/2 \cdot DC \cdot DE \cdot \\sin (hat{EDC}) = 1/2 \cdot 2 \cdot frac(26)(21) \cdot frac(12)(13) = [/math]
[math]frac(24)(21) = 8/7 [/math]
Applicando di nuovo il teorema dei seni, possiamo ricavare il terzo lato del triangolo DEC:
[math] frac(CE)(\\sin (hat{EDC})) = frac(DC)(\\sin (hat{DEC})) [/math]
[math] CE = frac(DC \cdot \\sin (hat{EDC}))(\\sin(hat{DEC})) = frac(2 \cdot frac(12)(13))(frac(63)(65)) = [/math]
[math] frac(24)(13) \cdot frac(65)(63) = frac(40)(21) [/math]
Troviamo ora il perimetro:
[math]P_(DEC) = DC + CE + DE = 2 + frac(40)(21) + frac(26)(21) = [/math]
[math] frac(42 + 40 + 26)(21) = frac(108)(21) = frac(36)(7) [/math]