Introduzione alla trigonometria
La trigonometria comprende una serie di teoremi validi esclusivamente per i triangoli rettangoli ed altri per triangoli qualsiasi. Quando diciamo risolvere un triangolo intendiamo che vogliamo determinare tutti i suoi elementi: la misura dei tre lati, dei tre angoli, il perimetro, l'area ed eventualmente anche le misure degli elementi interni come altezza, mediana e bisettrice.Come si fa a risolvere un triangolo?
Bisogna applicare i teoremi della trigonometria in base al tipo di triangolo che si sta risolvendo e agli elementi noti.
La trigonometria ci fornisce dunque gli strumenti necessari per studiare le relazioni che intercorrono tra i lati e gli angoli di un triangolo sfruttando le funzioni goniometriche applicate caso per caso.
Per l'applicazione di un teorema qualsiasi bisogna conoscere almeno tre elementi del triangolo.
Per quanto riguarda il triangolo rettangolo esso per definizione ha un angolo retto e due angoli acuti questo significa che un elemento è sempre noto, l’angolo di 90°, e perciò bisogna conoscerne solo altri due.
Teoremi della trigonometria sui triangoli rettangoli
Di un triangolo rettangolo possono essere noti i seguenti elementi:- un lato e due angoli
- due lati e l'angolo fra essi compreso
- due lati e un angolo opposto a uno di essi
Primo teorema sui triangoli rettangoli
In un triangolo rettangolo, la misura di un cateto si ottiene come prodotto tra la misura dell'ipotenusa e il coseno dell'angolo acuto adiacente ad esso, oppure come prodotto tra la misura dell'ipotenusa e il seno dell'angolo opposto ad esso.
Scriviamo, in simboli matematici, le relazioni stabilite dal teorema:
- [math]b=a\cdot sin\beta=a\cdot cos \gamma[/math]
- [math]c=a \cdot sin\gamma=a\cdot cos \beta[/math]
- [math]a=\frac{b}{sin\beta}=\frac{b}{cos \gamma}[/math]
- [math]a=\frac{c}{cos\beta}=\frac{c}{sin \gamma}[/math]
in ogni triangolo rettangolo, la misura dell'ipotenusa è uguale al quoziente tra la misura di un cateto e il coseno dell'angolo adiacente (al cateto) o al seno dell'angolo opposto (al cateto).
Secondo teorema:
In ogni triangolo rettangolo la misura di un cateto è uguale a quella dell'altro cateto moltiplicata per la tangente dell'angolo opposto al primo cateto, oppure per la cotangente dell'angolo acuto a esso adiacente. Rappresentiamo in simboli matematici, quanto affermato dal teorema:
- [math]b=c \cdot tan \beta = c \cdot cot \gamma[/math]
- [math]c=b \cdot cot \beta = b \cdot tan \gamma[/math]
Per ulteriori approfondimenti sulla risoluzione dei triangoli qualunque vedi qua
Quattro casi possibili sui triangoli rettangoli
Elenchiamo di seguito i quattro casi in cui è possibile applicare i due teoremi visti e dunque risolvere il triangolo rettangolo.- sono dati l'ipotenusa e un angolo acuto
- sono dati un cateto e l’angolo adiacente acuto
- sono dati l'ipotenusa e un cateto
- sono dati i due cateti
Questi teoremi della trigonometria si possono utilizzare anche quando il triangolo rettangolo è individuabile all'interno di altre figure piane.
Sempre con la trigonometria è impossibile calcolare l'area di un triangolo qualsiasi noti due suoi dati e il seno dell'angolo compreso tra essi.
Dato un triangolo di vertici A, B, C note le misure dei lati AB, e AC e il seno dell'angolo fra essi compreso, La formula per calcolare l'area è la seguente:
[math]Area=\frac{1}{2}\cdot \overline{AB} \cdot \overline{AC} \cdot sin \alpha[/math]
Questo terzo teorema ci consente di calcolare l'area di un triangolo qualsiasi, purché siano noti gli elementi indicati.
Per ulteriori approfondimenti sulla risoluzione dei triangoli rettangoli vedi qua
Problema svolto di trigonometria
Calcolare il perimetro di un triangolo rettangolo e l'area, conoscendo solo la misura di un cateto e il seno dell’angolo opposto ad esso.DATI
- [math]b=24cm[/math]
- [math]sin \beta={12\over 13}[/math]
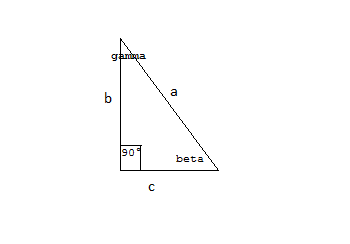
Noto il cateto b e noto il seno dell’angolo
[math]\beta[/math]
ad esso opposto, possiamo calcolare la misura dell’ipotenusa [math]a[/math]
.Dobbiamo dividere la misura del cateto per il seno dell’angolo opposto:
[math]a=\frac{b}{sin\beta}=\frac{24}{12\over 13}[/math]
[math]a=\frac{24}{12\over 13}[/math]
[math]a=24\cdot {13\over 12}[/math]
[math]a=26 cm[/math]
La lunghezza dell’ipotenusa è di 26 cm.
Per calcolare l’altro cateto usiamo sempre l’angolo
[math]\beta[/math]
, ma il suo coseno:
[math]c=a\cdot cos \beta[/math]
Il coseno lo ricaviamo utilizzando la seconda relazione fondamentale della goniometria:
[math]sin^2 \beta+cos^2 \beta=1[/math]
[math]cos \beta=\pm \sqrt{1-sin^2 \beta}[/math]
[math]cos \beta=\pm \sqrt{1-\frac{144}{169}}[/math]
[math]cos \beta=\pm \sqrt{25\over 169}[/math]
Ricordiamo che gli angoli
[math]\gamma[/math]
e [math]\beta[/math]
ono acuti, quindi [math]0, perciò escludiamo la soluzione negativa, in quanto l'angolo si trova nel primo quadrante della circonferenza goniometrica:
[math]cos \beta={5\over 13}[/math]
Ed ora calcoliamo la misura dell’altro cateto:
[math]c=26cm\cdot {5\over 13}[/math]
[math]c=10cm [/math]
Naturalmente potevamo applicare anche il teorema di Pitagora, avremmo ottenuto lo stesso risultato. Possiamo verificare:
[math]c=\sqrt {a^2-b^2}[/math]
[math]c=\sqrt {26^2-24^2}[/math]
[math]c=\sqrt {100}=10 cm[/math]
Abbiamo trovato la misura dei tre lati ed ora possiamo calcolare sia il perimetro che l'area. Per il perimetro abbiamo:
[math]2p=a+b+c=26cm+24cm+10cm=60cm[/math]
Per l’area, effettuiamo il semiprodotto dei due cateti:
[math]Area=\frac{1}{2}b\cdot c[/math]
[math]Area=120 cm^2[/math]
Per ulteriori approfondimenti sulle funzioni goniometriche seno e coseno vedi qua
