Determinare il perimetro di un triangolo isoscele di base
[math]12cm[/math]
e co l'angolo al vertice di [math]36^circ[/math]
. Svolgimento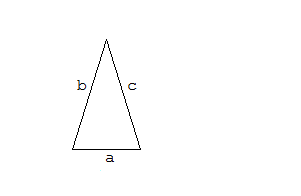
Dati
[math]a=12cm[/math]
[math]alpha=36^circ[/math]
[math]b=c[/math]
Poichè la somma degli angoli interni di un triangolo è di
[math]180^circ[/math]
, ovvero[math]alpha+eta+gamma=180^circ[/math]
si ha che
[math]36^circ+eta+gamma=180^circ => eta+gamma=180^circ-36^circ=144^circ[/math]
.Il triangolo isoscele ha gli angoli alla base uguali, quindi se
[math]eta+gamma==144^circ => eta=gamma=(144^circ)/2=72^circ[/math]
. In un triangolo il rapporto di due lati eguaglia il rapporto tra il seno degli angoli ad essi opposti
[math]a/b=(\\sin (alpha))/(\\sin(eta))[/math]
Pertanto
[math]b=(a\\sin (alpha))/(\\sin(eta))=(12cm \cdot \\sin(36^circ))/(\\sin(72^circ))=11,41cm[/math]
.Il triangolo è isoscele, quindi
[math]b=c=11,41cm[/math]
.Pertanto il perimetro del triangolo, dato dalla somma dei lati
[math]2p=a+b+c=(12+11,41+11,41)cm=34,82cm[/math]
.