Calcolare il perimetro di un triangolo rettangolo, sapendo che l'area è di
[math]24cm^2[/math]
e [math]tg(eta)=3/4[/math]
. Svolgimento
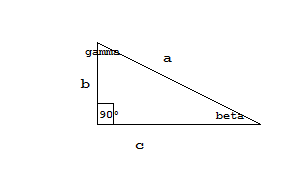
Dati
[math]alpha=90^circ[/math]
[math]A=24cm^2[/math]
[math]tg(eta)=3/4[/math]
Sappiamo che
[math]tg(eta)=3/4 => eta=arctg(3/4)=36,87^circ[/math]
.Quindi poichè la somma degli angoli interni di un triangolo è di
[math]180^circ[/math]
, ovvero[math]alpha+eta+gamma=180^circ[/math]
si ha che
[math]90^circ+36,87^circ+gamma=180^circ => gamma=180^circ-90^circ-36,87^circ=53,13^circ[/math]
.Pertanto
[math]gamma=53,13^circ[/math]
. In un triangolo rettangolo un cateto è uguale al prodotto dell'ipotenusa
per il seno dell'angolo opposto al cateto stesso.
[math]b=a\\sin (eta)[/math]
, inoltre l'area di un triangolo è data dal semiprodotto di due lati per il seno dell'angolo compreso:[math]A=1/2ab(\\sin (gamma))=24cm^2[/math]
.Mettiamo a sistema le due equazioni ricavate e riolviamolo per sostituzione
[math]\begin{cases} 1/2ab(\\sin (gamma))=24cm^2 \\ b=a\\sin(eta) \ \end{cases}[/math]
;[math]\begin{cases} 1/2a(a\\sin (eta))\\sin(gamma)=24 \\ b=a\\sin (eta) \ \end{cases}[/math]
;[math]\begin{cases} 1/2a^2\\sin (eta)\\sin(gamma)=24 \\ b=a\\sin(eta) \ \end{cases}[/math]
;[math]\begin{cases} a^2=(24 \cdot 2)/(\\sin (eta)\\sin(gamma)) \\ b=a\\sin(eta) \ \end{cases}[/math]
;[math]\begin{cases} a^2=(48)/(\\sin (36 & 13^circ)) \\ b=a\\sin(eta) \ \end{cases}[/math]
;[math]\begin{cases} a^2=100 \\ b=a\\sin (eta) \ \end{cases}[/math]
;[math]\begin{cases} a=10 \\ b=10 \cdot \\sin (36 & 87^circ) \ \end{cases}[/math]
;[math]\begin{cases} a=10 \\ b=6 \ \end{cases}[/math]
. Per il Teorema di pitagora
[math]c=\sqrt{a^2-b^2}=\sqrt((10cm)^2-(6cm)^2)=\sqrt((100cm^2)-(36cm^2))=\sqrt(64)cm=8cm[/math]
.Pertanto il perimetro del triangolo, dato dalla somma dei lati
[math]2p=a+b+c=(10+6+8)cm=24cm[/math]
.


