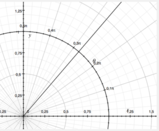
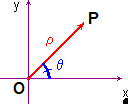
Le coordinate polari sono un sistema di coordinate nel piano determinato da un punto
[math]O[/math]
, detto polo, e da una semiretta avente origine in [math]O[/math]
detta asse polare. Un generico punto [math]P[/math]
del piano è univocamente determinato da due parametri 1) la distanza dal polo, cioè la lunghezza del segmento
[math]PO[/math]
, indicata con [math]
ho[/math]
ho[/math]
2) la misura in radianti dell'angolo, indicata con
[math] heta[/math]
, che l'asse polare forma con la retta [math]OP[/math]
, partendo da [math]O[/math]
e spostandosi in senso antiorario. Da questo si deduce che
[math]
ho in mathbb{R}^+[/math]
e ho in mathbb{R}^+[/math]
[math] heta in [0, 2 \pi)[/math]
(o comunque in ogni altro intervallo [math][a, b)[/math]
tale che [math]b - a = 2 \pi[/math]
). 
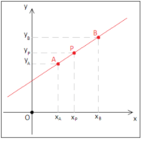
Si può passare dalle coordinate polari
[math](
ho, heta)[/math]
alle coordinate cartesiane ho, heta)[/math]
[math](x,y)[/math]
mediante queste relazioni
[math]\begin{cases} x =
ho \\cos( heta) \\ y =
ho \\sin ( heta) \ \end{cases}[/math]
ho \\cos( heta) \\ y =
ho \\sin ( heta) \ \end{cases}[/math]
Analogamente si può passare dalle coordinate cartesiane alle polari osservando che
[math]
ho = \sqrt{x^2 + y^2}[/math]
e che, considerando ho = \sqrt{x^2 + y^2}[/math]
[math] heta in [0, 2 \pi)[/math]
[math] heta = \begin{cases} \text{arctg}(frac{y}{x} & quad \text{se } x > 0 \text{ e } y ge 0 \\ \text{arctg}(frac{y}{x}) + 2 \pi & quad \text{se } x > 0 \text{ e } y > 0 \\ \text{arctg}(frac{y}{x}) + \pi & quad \text{se } x 0 \\ frac{3 \pi}{2} & quad \text{se } x = 0 \text{ e } y
Esempio
Equazione della circonferenza: l'equazione di una circonferenza in coordinate polari con centro in
[math](
ho_0, heta_0)[/math]
e raggio ho_0, heta_0)[/math]
[math]R[/math]
è
[math]
ho^2 + 2
ho
ho_0 \\cos( heta - heta_0) +
ho_0^2 = R^2[/math]
ho^2 + 2
ho
ho_0 \\cos( heta - heta_0) +
ho_0^2 = R^2[/math]
