Le equazioni
Le equazioni, ovvero uguaglianze matematiche composte da espressioni matematiche, possono differenziarsi in base alle tipologie di incognite e funzioni presenti all'interno dell'equazione stessa:- Equazioni reali;
- Equazioni fratte;
- Equazioni irrazionali;
- Equazioni logaritmiche;
- Equazioni trigonometriche;
- Equazioni esponenziali.
Per ulteriori approfondimenti sulle equazioni, cosa sono e come si risolvono vedi qui
Equazioni fratte
Un'equazione è definita fratta se è composta da frazioni algebriche presenti o al primo o al secondo o in entrambi i membri dell'equazione, in cui è presente l'incognita o al numeratore o al denominatore della frazione stessa.La forma generale è la seguente:
Dove:
- [math]N(x)[/math]è il numeratore della frazione;
- [math]D(x)[/math]è il denominatore della frazione.
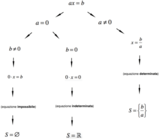
L'equazione fratta così come qualsiasi equazione può essere:
- Equazione fratta determinata: si ha se e solo se l'equazione ammette una ed una sola soluzione, o più soluzioni;
- Equazione fratta indeterminata: si ha se e solo se l'equazione ammette infinito di soluzioni;
- Equazione fratta impossibile: si ha se e solo se l'equazione non ammette soluzioni.
La soluzione di un equazione fratta
La forma generale di un'equazione fratta è la seguente riportata:
Dove:
- [math]a(x), b(x), c(x)[/math]e[math] d(x)[/math]sono polinomi generici, o anche funzioni più complesse.
L'insieme di definizione dell'equazione generale fratta viene riportata come di seguito:
La soluzione è stata ottenuto andando a supporre che
Si procede alla risoluzione andando a moltiplicare ambo i membri per
La soluzione dell'equazione fratta iniziale è data dall'insieme di tutte le
Esempio di risoluzione equazione fratte
Sia data la seguente equazione fratta e si voglia procedere alla sua risoluzione:
Si osserva subito che le condizioni di esistenza risulta essere:
Una volta individuato l'insieme di esistenza dell'equazione fratta, si procedere andando a moltiplicare ambo i membri per:
Da cui, si ottiene l'equazione riportata di seguito:
Entrambe le soluzioni dell'equazione fratta trovate sono diverse da
Equazioni irrazionali
Un'equazione è definita irrazionale se è composta da espressioni algebriche che sono poste sotto radice presenti o al primo o al secondo o in entrambi i membri dell'equazione, in cui è presente l'incognita all'interno della radice stessa.La forma generale è la seguente:
Dove risulta:
- [math]f(x)[/math]è un polinomio a coefficienti appartenenti all'insieme dei numeri reali;
- [math]g(x)[/math]è un polinomio a coefficienti appartenenti all'insieme dei numeri reali.
L'equazione irrazionale così come qualsiasi equazione può essere:
- Equazione irrazionale determinata: si ha se e solo se l'equazione ammette una ed una sola soluzione, o più soluzioni;
- Equazione irrazionale indeterminata: si ha se e solo se l'equazione ammette infinito di soluzioni;
- Equazione irrazionale impossibile: si ha se e solo se l'equazione non ammette soluzioni.
La soluzione di un equazione irrazionale
La forma generale di un'equazione fratta è la seguente riportata:
L'insieme di definizione dell'equazione irrazionale dipende dall'ordine della radice. Deve essere chiaro che n non possa essere pari a zero, da cui val che
Possiamo differenziare la soluzione dell'equazione irrazionale in due casistiche:
- [math]n[/math]risulta essere un numero intero pari: in questo caso l'insieme di definizione dell'equazione prevede che tutto quello che è all'interno della radice pari debba essere necessariamente sempre maggiore o uguale a zero;
- [math]n[/math]risulta essere un numero intero dispari: in questo caso l'insieme di definizione dell'equazione prevede che tutto quello che è all'interno della radice dispare possa appartenere all'insieme dei numeri reali, senza alcuna restrizione del campo di esistenza
- 1° caso: se [math]n[/math]è dispari, allora l'insieme di definizione[math]D[/math]coincide con l'insieme in cui sono ben definite[math]f(x)[/math]e[math]g(x)[/math];
2° caso: se
Una volta che è stato determinato l'insieme del campo di esistenza dell'equazione irrazionale pari a
Si procede elevando ambo i membri alla potenza
La soluzione dell'equazione iniziale andrà a coincidere con l'insieme delle
Esempio di risoluzione equazione irrazionale
Sia data la seguente equazione irrazionale e si voglia procedere alla sua risoluzione:

Visto e considerato che l'ordine della radice è di ordine pari, allora si ottiene che l'insieme di definizione risulti essere pari a :
l'insieme di definizione è stato ottenuto andando a porre tutto quello sotto radice maggiore e uguale a zero, e individuandone le soluzioni.
Avendo individuato l'insieme di definizione, si può procedere alla risoluzione dell'equazione irrazionale andando ad elevare ambo i membri al quadrato, da cui si ottiene la seguente equazione:
La soluzione dell'equazione risulta dunque essere pari a:
Dato che