Anteprima
Vedrai una selezione di 1 pagina su 3
Disdici quando
vuoi
vuoi
Acquista con carta
o PayPal
o PayPal
Scarica i documenti
tutte le volte che vuoi
tutte le volte che vuoi
Sintesi
Nel seguente appunto sono elencate formule di trigonometria utili per la risoluzione dei triangoli e per il calcolo di elementi caratteristici di questi ultimi, per ogni tipo di triangolo, anche non necessariamente rettangolo. Per applicare queste formule bisogna conoscere le definizioni di seno, coseno, tangente e cotangente. Per comodità di notazione, chiameremo [math]AB=c, BC=a, CA=b[/math]
, in altre parole, con ogni lettera minuscola indichiamo il lato opposto ad un certo vertice (scritto però in lettera maiuscola). Introduzione alla trigonometria: triangolo rettangolo
In un triangolo rettangolo
[math]ABC[/math]
, retto in [math]A[/math]
, ponendo [math]AB=c, BC=a, CA=b[/math]
e, per quanto riguarda gli angoli [math]\widehat{BAC}=\alpha, \widehat{ABC}=\beta, \widehat{ACB}=\gamma[/math]
valgono le seguenti relazioni:Per quanto riguarda il cateto
[math]b[/math]
si hanno le uguaglianze [math]b=a\sin(\beta)=a\cos(\gamma)=c\tan(\beta)=c\cot(\gamma)[/math]
Per quanto riguarda il cateto
[math]c[/math]
si hanno invece le uguaglianze[math]c=a\cos(\beta)=a\sin(\gamma)=b\cot(\beta)=b\tan(\gamma)[/math]
Come abbiamo potuto vedere, ci sono addirittura 4 modi diversi per risalire dall'ipotenusa ad uno dei cateti, praticamente un modo per ogni funzione goniometrica precedentemente elencata: seno, coseno, tangente e cotangente.
Per approfondimenti su seno e coseno vedi anche qua
Teorema della corda
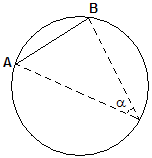
Sia
[math]R[/math]
il raggio di una qualsiasi circonferenza, e sia [math]alpha[/math]
l'ampiezza dell'angolo alla circonferenza sotteso dalla corda [math]AB[/math]
, allora la lunghezza di [math]AB[/math]
è pari, per il Teorema della Corda, a: [math]AB=2Rsin(\alpha)[/math]
Questo teorema permette di dimostrare che in un triangolo rettangolo il circocentro sta sull'ipotenusa. Se consideriamo infatti un triangolo rettangolo di ipotenusa
[math]AB[/math]
, avremo [math]\alpha=90^{\circ}[/math]
, e applicando il teorema della corda, avremo che [math]AB=2Rsin(\alpha)=2Rsin(90^{\circ})=2R[/math]
, quindi [math]AB[/math]
è un diametro, di conseguenza contiene il circocentro del triangolo rettangolo in questione, come volevasi dimostrare.Triangolo generico - Introduzione e notazione
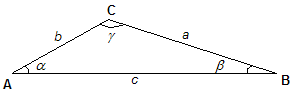
Poniamo nuovamente
[math]AB=c, BC=a, CA=b[/math]
per i lati, e [math]\widehat{BAC}=\alpha, \widehat{ABC}=\beta, \widehat{ACB}=\gamma[/math]
per gli angoli.Per qualsiasi triangolo, sia esso rettangolo, ottusangolo o acutangolo, valgono le seguenti formule:
Area di un generico triangolo
Detta
[math]S[/math]
l'area abbiamo:[math]S=\frac{1}{2}ab\sin(\gamma)=\frac{1}{2}bc\sin(\alpha)=\frac{1}{2}ca\sin(\beta)[/math]
.In sintesi, è sempre possibile determinare l'area di un triangolo se conosciamo due lati qualsiasi e l'angolo compreso tra questi.
Teorema dei seni e relazione con il Teorema della corda
Il rapporto fra la lunghezza di un lato e il seno dell'angolo ad esso opposto è costante e pari al doppio del raggio (o diametro) della circonferenza circoscritta al triangolo
[math]ABC[/math]
(potremmo pensare al Teorema dei Seni come una formula inversa del Teorema della Corda precedentemente citato), cioè:[math]\frac{a}{\sin (alpha)} = \frac{b}{\sin(beta)} = \frac{c}{\sin(gamma)}=2R[/math]
Teorema del coseno (detto anche Teorema di Carnot o Teorema di Pitagora generalizzato)
In ogni triangolo valgono le seguenti relazioni:
[math]a^2 = b^2 + c^2 - 2 bc \cos(\alpha)[/math]
e similmente:[math]b^2 = a^2 + c^2 - 2 ac \cos(\beta)[/math]
[math]c^2 = a^2 + b^2 - 2 ab \cos(\gamma)[/math]
Tale Teorema è noto anche come Teorema di Pitagora generalizzato poiché, il Teorema di Pitagora non è altro che un caso particolare del Teorema di Carnot. Se per esempio
[math]\alpha=90^{\circ}[/math]
, allora [math]a^2=b^2+c^2-2bc \cos(90^{\circ})=b^2+c^2[/math]
, che è proprio il Teorema di Pitagora in quanto il coseno dell'angolo retto è nullo.Teorema delle proiezioni:
In ogni triangolo valgono le seguenti relazioni:
[math]a=b\cos(\gamma)+c\cos(\beta)[/math]
[math]b=a\cos(\gamma)+c\cos(\alpha)[/math]
[math]c=b\cos(\alpha)+a\cos(\beta)[/math]
Tali formule si dimostrano facilmente tracciando l'altezza uscente dal vertice opposto al lato preso in esame e considerando i due triangoli rettangoli che si formano, utilizzando le formule citate nel primo paragrafo.
Formule di Briggs - Relazioni tra seno, coseno e lati del triangolo
chiamando con[math]p = \frac{a+b+c}{2}[/math]
il semiperimetro, in ogni triangolo valgono le seguenti formule di Briggs
[math]\sin (\frac{\alpha}{2}) = \sqrt{\frac{(p-b)(p-c)}{bc}}[/math] | [math]\cos(\frac{\alpha}{2}) = \sqrt{\frac{p(p-a)}{bc}}[/math] |
[math]\sin (\frac{\beta}{2}) = \sqrt{\frac{(p-a)(p-c)}{ac}}[/math] | [math]\cos(\frac{\beta}{2}) = \sqrt{\frac{p(p-b)}{ac}}[/math] |
[math]\sin (\frac{\gamma}{2}) = \sqrt{\frac{(p-a)(p-b)}{ab}}[/math] | [math]\cos(\frac{\gamma}{2}) = \sqrt{\frac{p(p-c)}{ab}}[/math] |
Raggio del cerchio inscritto
In ogni triangolo, detta
[math]S[/math]
l'area e [math]p[/math]
il semiperimetro, il raggio del cerchio inscritto, detto anche [math]r[/math]
vale
[math]r = \frac{A}{p} = (p - a) \tan (\frac{\alpha}{2}) = (p-b) \tan (\frac{\beta}{2}) = (p-c) \tan(\frac{\gamma}{2})[/math]
Raggio del cerchio circoscritto
In ogni triangolo di area
[math]S[/math]
il raggio del cerchio circoscritto, detto anche [math]R[/math]
vale
[math]R = \frac{a}{2 \sin (\alpha)} = \frac{b}{2 \sin(\beta)} = \frac{c}{2 \sin(\gamma)} = \frac{abc}{4S}[/math]
Si noti come queste formule (eccetto l'ultima) sono in realtà delle formule inverse del Teorema della Corda e del Teorema dei Seni.
Raggio della circonferenza exinscritta tangente, rispettivamente, ai lati di misura a,b,c
L'ex-cerchio è una circonferenza esterna al triangolo, tangente ad uno dei lati e ai prolungamenti degli altri 2. Esiste un'omotetia di centro un vertice che manda il cerchio inscritto nell'ex-cerchio del rispettivo vertice. Detti
[math]r_a, r_b, r_c[/math]
i raggi degli ex-cerchi tangenti rispettivamente ai lati [math]a,b,c[/math]
si ha, detta [math]S[/math]
l'area del triangolo e [math]p[/math]
il semiperimetro:[math]r_a = \frac{S}{p - a}[/math]
[math]r_b = \frac{S}{p - b}[/math]
[math]r_c = \frac{S}{p - c}[/math]
Lunghezza della mediana relativa, rispettivamente, ai lati di misura a,b,c
Si hanno le relazioni:
[math]m_a = \frac{1}{2} \sqrt{2 b^2 + 2 c^2 - a^2}[/math]
[math]m_b = \frac{1}{2} \sqrt{2 a^2 + 2 c^2 - b^2}[/math]
[math]m_c = \frac{1}{2} \sqrt{2 a^2 + 2 b^2 - c^2}[/math]
Si ricorda che la mediana di un triangolo è quel segmento che congiunge uno dei vertici del triangolo col punto medio del lato opposto a tale vertice.
Lunghezza della bisettrice uscente, rispettivamente, dai vertici A, B, C:
Si hanno le relazioni:
[math]b_{A} = \frac{2 bc \cos(\frac{\alpha}{2})}{b + c}[/math]
[math]b_{B} = \frac{2 ac \cos(\frac{\beta}{2})}{a + c}[/math]
[math]b_{C} = \frac{2 ab \cos(\frac{\gamma}{2})}{a + b}[/math]
Si ricorda che la bisettrice di un angolo è quella retta che divide l'angolo in due angoli congruenti.
Estratto del documento
Formule di addizione e sottrazione:
β)
sen(α + = senαcosβ + cosαsenβ
β)
sen(α - = senαcosβ - cosαsenβ
β)
cos(α + = cosαcosβ - senαsenβ
β)
cos(α - = cosαcosβ + senαsenβ
α β
+
tg tg
α β
+ =
( )
tg α β
−
1 tg tg
α β
−
tg tg
α β
− =
( )
tg α β
+
1 tg tg
Formule di duplicazione: α=β)
(si ottengono dalle precedenti con
sen 2α = 2senαcosα
α α= α α
2 2 2 2
- sen 1 – 2sen = 2cos -1
cos 2α = cos α
2
tg
α =
2
tg α
− 2
1 tg
Formule di bisezione:
α α
−
1 cos
= ±
sin 2 2
α α
+
1 cos
= ±
cos 2 2
α α α α
−
−
1 cos 1 cos sin
= =
= ±
tg α α α
+ +
2 1 cos sin 1 cos
Formule parametriche:
t
2
α =
sin + 2
t
1 − 2
t
1
α =
cos + 2
t
1 t
2
α =
tg − 2
t
1 α
=
ove t tg 2
Formule di prostaferesi:
+ −
p q p q
+ =
sin p sin q 2 sin cos
2 2 by Skuola.net
Dettagli
