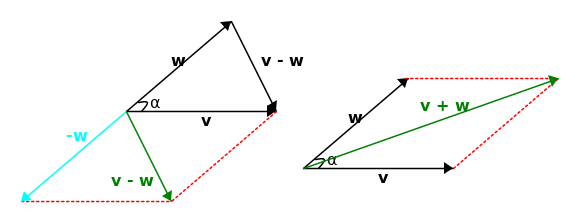
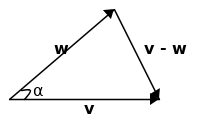
Procediamo con una dimostrazione abbastanza semplice, facendo riferimento alla seguente figura:
figura
.
Si definisce prodotto scalare l'applicazione $\cdot \:\mathbb{R}^{\text{3}}\times\mathbb{R}^{\text{3}} \mapsto \mathbb{R}$ che associa ai vettori v e w lo scalare $\mathbf{v}\cdot\mathbf{w}$
Nella nostra analisi tornerà utile anche la definizione di norma euclidea di un vettore
v:
$|| \mathbf{v} ||:=\sqrt{\mathbf{v}\cdot \mathbf{v}}$
Osservando la figura (considerando implicitamente alcune proprietà del prodotto scalare) notiamo che:
$|| \mathbf{v}-\mathbf{w} ||^{2}=(\mathbf{v}-\mathbf{w})\cdot (\mathbf{v}-\mathbf{w})=|| \mathbf{v} ||^{2}+|| \mathbf{w} ||^{2} -2\mathbf{v}\cdot \mathbf{w}$
Inoltre, applicando il teorema dei coseni al triangolo riportato in figura:
$|| \mathbf{v}-\mathbf{w} ||^{2}=(\mathbf{v}-\mathbf{w})\cdot (\mathbf{v}-\mathbf{w})=|| \mathbf{v} ||^{2}+|| \mathbf{w}||^{2} -2|| \mathbf{v} |||| \mathbf{w} ||\cos(\alpha )$
Uguagliando i secondi membri delle due precedenti relazioni:
$|| \mathbf{v} ||^{2}+|| \mathbf{w}||^{2} -2\mathbf{v}\cdot \mathbf{w}=|| \mathbf{v}||^{2}+|| \mathbf{w} ||^{2} -2|| \mathbf{v}|||| \mathbf{w}||\cos(\alpha )$
e semplificando
$\mathbf{v}\cdot \mathbf{w}=|| \mathbf{v} |||| \mathbf{w} ||\cos(\alpha )$
$square$
Dal punto di vista geometrico puoi interpretare il prodotto scalare come proiezione ortogonale del vettore
w sulla retta parallela al vettore
v.
Questa interpretazione e' utilissima per comprendere meglio il significato di lavoro.
La forza ortogonale alla traiettoria (di spostamento) non compie lavoro; la forza parallela si'.
Interpretando
w come una forza e
v come uno spostamento, allora stai calcolando la componente parallela a
v utile al lavoro.