Il seguente è un albero binario decisionale relativo al problema dell'ordinamento con scambio.
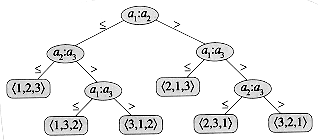
Ora il numero di foglie è dato da tutte le possibili disposizioni ovvero \(\displaystyle n! \), se l'albero fosse completo (ogni nodo ha 2 figli) allora il numero di foglie sarebbe \(\displaystyle 2^h \) dove \(\displaystyle h \) è l'altezza.
Quindi si può dire che \(\displaystyle 2^h\geq n! \)
che si può riscrivere come \(\displaystyle 2^h\geq n(n-1)(n-2) \dots2 \cdot 1\)
Ed ecco il passaggio che non capisco: \(\displaystyle 2^h\geq n(n-1)(n-2) \dots2 \cdot 1 \geq \frac{n}{2}^\frac{n}{2}\)
Il resto invece mi è chiaro:
\(\displaystyle 2^h \geq \frac{n}{2}^\frac{n}{2} \)
\(\displaystyle h \geq \log_{2}(\frac{n}{2}^\frac{n}{2}) \)
\(\displaystyle h = \Omega(n log_{2}n) \)
Un altro modo di dimostrare il tutto è il seguente: file (pagina 2)
Qui invece non mi è chiaro come si arriva al seguente step \(\displaystyle \geq 0 + \sum\limits_{i=\frac{n}{2}}^n \log_{2}{\frac{n}{2}} \)
e al successivo \(\displaystyle \frac{n}{2}\log_{2}{\frac{n}{2}} \)
Grazie mille

