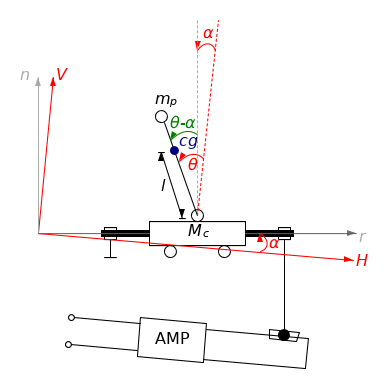
Si tratta di un pendolo inverso incernierato su di un carrello. Il pendolo è composto di una asta, libera di ruotare attorno al perno che la lega al carrello, e di una massa \(m_p\) applicata all'estremo superiore. L'angolo alla verticale formato dall'asta è \(\theta\). Il centro di massa \(\boldsymbol{r}_\text{cg}\) del pendolo si trova ad una distanza \(l\) dalla cerniera.
Il carrello, di massa \(M_c\), è in grado di muoversi lungo delle rotaie, le quali sono inclinate di un angolo \(\alpha\) rispetto l'orizzontale. La posizione del carrello lungo le rotaie è \(r\).
Al carrello può essere applicata una forza arbitraria \(au\) parallela alle rotaie, mentre al pendolo un momento baricentrico arbitrario \(\tau\). Sul sistema agiscono inoltre delle forze di attrito di tipo viscoso e coulombiano.
Le equazioni che vorrei ricavare sono le seguenti:
\[\boxed{\begin{aligned}
(1)\quad & (M_c+m_p)\ddot{r}-m_pl\cos(\theta-\alpha)\ddot{\theta}+m_pl\sin(\theta-\alpha)\dot{\theta}^2+(M_c+m_p)g\sin\alpha+b\dot{r}+F_s\text{sign}(\dot{r})=au \\
(2)\quad &(J_p+m_pl^2)\ddot{\theta}-m_pl\cos(\theta-\alpha)\ddot{r}-m_pgl\sin\theta+c\dot{\theta}=\tau
\end{aligned}}\]
Con \(\text{sign}\) si intende la funzione segno, mentre \(b\), \(c\) sono i coefficienti di attrito viscoso a cui sono sottoposti carrello e pendolo, e \(F_s\) è il coefficiente di attrito coulombiano. Con \(J_p\) si intende il momento di inerzia baricentrico dell'asta.
Per dedurre tali equazioni seguo l'approccio lagrangiano. Le coordinate libere sono \(r\) e \(\theta\), per cui le equazioni di Lagrange, tendo conto delle varie forze non conservative in gioco, dovrebbero essere
\[\begin{aligned}
(3) \quad & \frac{\text{d}}{\text{d}t} \frac{\partial \mathcal{L}}{\partial \dot{r}}-\frac{\partial \mathcal{L}}{\partial r}=au-b\dot{r}-F_s\text{sign}(\dot{r}) \\
(4) \quad & \frac{\text{d}}{\text{d}t} \frac{\partial \mathcal{L}}{\partial \dot{\theta}}-\frac{\partial \mathcal{L}}{\partial \theta}=\tau-c\dot{\theta} \\
\end{aligned}\]
Procedo quindi nel determinare la lagrangiana del sistema. Come sistema di riferimento assumo quello individuato dalle rotaie, per cui ridisegno il sistema in tale sistema di riferimento. La verticale e l'orizzontale sono indicate con H e V.
La lagrangiana \(\mathcal{L}\) è data dalla differenza tra l'energia cinetica \(T\) e dell'energia potenziale \(U\) del sistema, pertanto per prima cosa mi ricavo le espressioni di \(T\) e \(U\).
L'energia cinetica \(T\) del sistema è data la somma dell'energia cinetica del carrello \(T_c=1/2M_c\dot{r}^2\) e dell'energia cinetica del pendolo \(T_p=1/2m_pv_{\text{cg}}^2+1/2J_p{\dot{\theta}}\!\phantom{,}^2\). L'espressione esplicita della velocità del centro di massa del pendolo la determino derivando rispetto al tempo la posizione del centro di massa del pendolo
\[\begin{aligned}
&\boldsymbol{r}_\text{cg}=[r-l\sin(\theta-\alpha)]\boldsymbol{u}_r+l\cos(\theta-\alpha)\boldsymbol{u}_n\\
&\boldsymbol{v}_\text{cg}=[\dot{r}-l\cos(\theta-\alpha)\dot{\theta}]\boldsymbol{u}_r-l\sin(\theta-\alpha)\dot{\theta}\boldsymbol{u}_n\\
&v_\text{cg}^2=\dot{r}^2+l^2\dot{\theta}\!\phantom{,}^2-2l\cos(\theta-\alpha)\dot{r}\dot{\theta}
\end{aligned}\]
In totale, l'energia cinetica del sistema è dunque pari a
\[(5) \quad T=\frac{1}{2}M_c\dot{r}^2+\frac{1}{2}m_p[\dot{r}^2+l^2\dot{\theta}\!\phantom{,}^2-2l\cos(\theta-\alpha)\dot{r}\dot{\theta}]+\frac{1}{2}J_p\dot{\theta}^2\]
Per quanto riguarda l'energia potenziale, l'unica forza conservativa agente sul sistema è la gravità, per tanto sia per il carrello che per il pendolo si ha \(U=-mgh\), dove \(m\) è la massa del corpo in questione e \(h\) è la quota del centro di massa del corpo in questione.
\[\begin{aligned}
&U_c=-M_cgr\sin\alpha \\
&U_p=-m_pg[r\sin\alpha+l\cos\theta]
\end{aligned}\]
In totale, l'energia potenziale del sistema è dunque pari a
\[(6) \quad U=-(M_c+m_p)gr\sin\alpha-m_pgl\cos\theta\]
Conseguentemente, in base alla \((5)\) e la \((6)\), la lagrangiana del sistema assume la forma
\[(7) \quad\mathcal{L}=\frac{1}{2}M_c\dot{r}^2+\frac{1}{2}m_p[\dot{r}^2+l^2\dot{\theta}\!\phantom{,}^2-2l\cos(\theta-\alpha)\dot{r}\dot{\theta}]+\frac{1}{2}J_p\dot{\theta}^2+(M_c+m_p)gr\sin\alpha+m_pgl\cos\theta\]
A questo punto non resta che inserire la \((7)\) nella \((3)\) e nella \((4)\). Il calcolo dei primi membri mi restituisce
\[\begin{aligned}
&\frac{\text{d}}{\text{d}t} \frac{\partial \mathcal{L}}{\partial \dot{r}}-\frac{\partial \mathcal{L}}{\partial r}=(M_c+m_p)\ddot{r}+m_pl\sin(\theta-\alpha)\dot{\theta}^2-m_pl\cos(\theta-\alpha)\ddot{\theta}-(M_c+m_p)g\sin\alpha \\
&\frac{\text{d}}{\text{d}t} \frac{\partial \mathcal{L}}{\partial \dot{\theta}}-\frac{\partial \mathcal{L}}{\partial \theta}=(J_c+m_pl^2)\ddot{\theta}+m_pl\sin(\theta-\alpha)\dot{\theta}\dot{r}-m_pl\cos(\theta-\alpha)\ddot{r}-m_plg\sin\theta\\
\end{aligned}\]
uguagliando ai secondi membri, e riarrangiando i termini, ottengo finalmente
\[\boxed{\begin{aligned}
(8) \quad &(M_c+m_p)\ddot{r}-m_pl\cos(\theta-\alpha)\ddot{\theta}+m_pl\sin(\theta-\alpha)\dot{\theta}^2-(M_c+m_p)g\sin\alpha+b\dot{r}+F_s\text{sign}(\dot{r})=au \\
(9) \quad &(J_c+m_pl^2)\ddot{\theta}-m_pl\cos(\theta-\alpha)\ddot{r}+m_pl\sin(\theta-\alpha)\dot{\theta}\dot{r}-m_plg\sin\theta+c\dot{\theta}=\tau\\
\end{aligned}}\]
I miei risultati \((8)\) e \((9)\) non sono in accordo con \((1)\) e \((2)\). La \((8)\) differisce dalla \((1)\) per il segno del termine potenziale \((M_c+m_p)g\sin\alpha\), mentre la \((9)\) differisce dalla \((2)\) per la presenza del termine \(m_pl\sin(\theta-\alpha)\dot{\theta}\dot{r}\). Non riesco a capire se sono io ad aver sbagliato qualcosa da qualche parte o se sono errate la \((1)\) e la \((2)\).
Ringrazio anticipatamente chiunque si cimenti nel problema per darmi una mano.