lo scopo di tale tutorial è il seguente:
Calcolare una stima di un generico integrale definito $int_(a)^(b)p(x)dx$ usando il metodo dell'Importance Sampling
a tale scopo prendiamo una opportuna pdf $f(x)$ in $[a,b]$ e riscriviamo l'integrale di partenza come
$int_(a)^(b)(p(x))/(f(x)) f(x)dx=\mathbb{E}[(p(x))/(f(x))]$
Quindi tale integrale si può stimare con $1/Nsum_(x=1)^N(p(x))/(f(x))$
Vediamo un esempio pratico:
Calcoliamo un'approssimazione del seguente integrale: $int_(0)^(1)e^(-x^2)dx$ utilizzando la funzione (tipo esponenziale) $e^(-x)$
Prima di tutto calcoliamo il valore esatto del nostro integrale per controllo. A tale scopo utilizziamo la distribuzione Gaussiana che è tabulata ovunque:
$int_(0)^(1)e^(-x^2)dx=sqrt(pi)int_(0)^(sqrt(2))1/sqrt(2pi)e^((-t^2)/2)dt=sqrt(pi)[Phi(sqrt(2))-1/2]~~0.7468$
La prima cosa da fare è normalizzare la funzione che vogliamo utilizzare come pdf. Quindi calcoliamo
$int_(0)^(1)e^(-x)dx=...=(e-1)/e$
quindi abbiamo trovato una pdf da usare:
$f(x)=e/(e-1)e^(-x)\mathbb{1}_([0;1])$
Per campionare da questa distribuzione invochiamo il teorema della trasformazione integrale; a tale scopo calcoliamo la CDF $F_X(x)$:
$F_X(x)=y=e/(e-1)int_(0)^(x)e^(-t)dt=...=e/(e-1)[1-e^(-x)]$
invertiamo la CDF trovata con semplici passaggi algebrici:
$x=-log[1-(e-1)/e y]$
abbiamo finito:
il campionamento delle y viene da una uniforme in $[0;1]$ e si trova dovunque, ad esempio su EXCEL con la formula CASUALE()
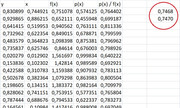
trasformiamo il campionamento dalla uniforme alla distribuzione voluta tramite $F^(-1)$ e stimiamo l'integrale facendo la media aritmetica dei rapporti $(p(x))/(f(x))$
Un campionamento con un migliaio di dati fatto or ora con Excel ha dato questa approssimazione: $0.7470$ contro $0.7468$...direi che ci siamo.
(cliccami per ingrandirmi)
saluti
