Ciao! Mi potreste mostrare come calcolare la potenza del test in questo esercizio?
"Il direttore di una palestra è interessato a determinare il numero di volte al mese che gli utenti accedono nella stanza X.
A tal fine, estrae un campione casuale di 16 utenti e nota che durante il mese, il numero medio di visite alla stanza X dei 16 utenti è stato di 11,2.
Assumendo che il numero di visite mensili alla stanza X sia distribuito come una variabile normale con varianza pari 12,96:
a)Sottoporre a verifica l'ipotesi che il numero medio mensile di accessi alla stanza X degli utenti della palestra non sia più di 10, al livello di significatività $alpha=0,05$
b)calcolare successivamente la potenza del test, assumendo che il numero medio reale di accessi mensili alla stanza X degli utenti della palestra sia 11".
Ho svolto il punto a con facilità.
Dato che
$z_t = 1,33$
e
$z_(0,05)=1,64$,
allora accetto l'ipotesi che il numero di accessi non sia più di 10.
Il mio problema riguarda il punto b.
Qualcuno potrebbe mostrarmi come risolverlo?
4 messaggi
• Pagina 1 di 1
Re: potenza del test
Il punto a) può essere risolto almeno in altri due modi diversi. Purtroppo (si fa per dire) conoscere altri metodi non è superfluo... 
Vediamo quindi come risolverlo diversamente da come hai fatto tu.
il punto critico che divide la regione di accettazione e di rifiuto è questo
$(bar(X)-10)/3.6 4=1.64$
da cui $bar(X)=11.48$
(quindi come giustamente hai osservato...accetti $H_0$ dato che $11.2<11.48$)
Ora però, con questa "regola di decisione" possiamo anche calcolare la potenza del test, ovvero la probabilità di rifiutare l'ipotesi $H_0$ quando è vera l'altra....ovvero quando la media è $11$
$gamma=mathbb{P}[bar(X)>=11.48|mu=11]=mathbb{P}[Z>=(11.48-11)/3.6 4]=mathbb{P}[Z>=0.53]~~30%$
graficamente....
(cliccami per ingrandirmi)
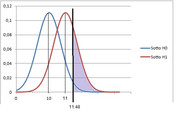
la potenza è l'area viola, mentre l'area a destra di 11.48 sotto la gaussiana blu è $alpha=5%$
Vediamo quindi come risolverlo diversamente da come hai fatto tu.
il punto critico che divide la regione di accettazione e di rifiuto è questo
$(bar(X)-10)/3.6 4=1.64$
da cui $bar(X)=11.48$
Regola di decisione
Rifiutiamo l'ipotesi $H_0$ se la media campionaria è $>=11.48$ mentre accettiamo l'ipotesi se la media campionaria è minore
(quindi come giustamente hai osservato...accetti $H_0$ dato che $11.2<11.48$)
Ora però, con questa "regola di decisione" possiamo anche calcolare la potenza del test, ovvero la probabilità di rifiutare l'ipotesi $H_0$ quando è vera l'altra....ovvero quando la media è $11$
$gamma=mathbb{P}[bar(X)>=11.48|mu=11]=mathbb{P}[Z>=(11.48-11)/3.6 4]=mathbb{P}[Z>=0.53]~~30%$
graficamente....
(cliccami per ingrandirmi)

la potenza è l'area viola, mentre l'area a destra di 11.48 sotto la gaussiana blu è $alpha=5%$
- tommik
- Moderatore

- Messaggio: 5401 di 11278
- Iscritto il: 23/04/2015, 13:13
- Località: Cassano Magnago
Re: potenza del test
tommik ha scritto:... calcolare la potenza del test, ovvero la probabilità di rifiutare l'ipotesi $H_0$ quando è vera l'altra.....
Chiedo per curiosità, in quanto "calcolare la potenza del test" penso che sia stato un argomento "scartato" nel mio corso di statistica.
Quindi, dopo aver fatto una verifica di ipotesi, calcolare la potenza del test significa valutare quanto la verifica di ipotesi sia stata efficace se la media fosse stata un valore specifico?
- anonymous_b7df6f
- Junior Member

- Messaggio: 97 di 490
- Iscritto il: 30/12/2019, 22:29
Re: potenza del test
tommik ha scritto:
Ora però, con questa "regola di decisione" possiamo anche calcolare la potenza del test, ovvero la probabilità di rifiutare l'ipotesi $H_0$ quando è vera l'altra....ovvero quando la media è $11$
$gamma=mathbb{P}[bar(X)>=11.48|mu=11]=mathbb{P}[Z>=(11.48-11)/3.6 4]=mathbb{P}[Z>=0.53]~~30%$
graficamente....
(cliccami per ingrandirmi)
Okay, quindi, generalizzando, dato un problema qualsiasi con:
$bar(x)$ =media campionaria
$sigma^2$=varianza
$r in RR$
$k in RR$
$alpha in RR$
e questo schema di ipotesi:
${H_0= mu_0 ; H_1 <r}$
se "salta fuori" che in realtà $mu$ è uguale ad un valore $k$, allora la potenza del test è uguale alla probabilità di rifiutare $H_0$ considerando che $mu=k$.
$text(potenza del test)= gamma= P[X<r | mu=k]$
è corretto?
- anonymous_f3d38a
- Average Member

- Messaggio: 212 di 902
- Iscritto il: 05/09/2019, 14:46
4 messaggi
• Pagina 1 di 1
Torna a Statistica e probabilità
Chi c’è in linea
Visitano il forum: Nessuno e 1 ospite