questo perché vedo \(S^1 \) come puntati. Ma l'esercizio mi chiede esplicitamente di calcolare il gruppo fondamentale del toro in un'altro modo e non riesco a trovare i buoni aperti con cui fare un ricoprimento del toro.
Calcoliamo il gruppo fondamentale del toro nel seguente modo:
1) Trovare un ricoprimento del toro \(T^2 \) con due aperti \(A, B \), con il secondo contrattibile ed identificare i tipi d'omotopia di \(A,B , A \cap B \).
2) Identificare i gruppi fondamentali di \(A,B \) e \( A \cap B \) e un omomorfismo indotto dall'inclusione \( A \cap B \subset A \)
3) Calcolare \( \pi_1 T^2 \).
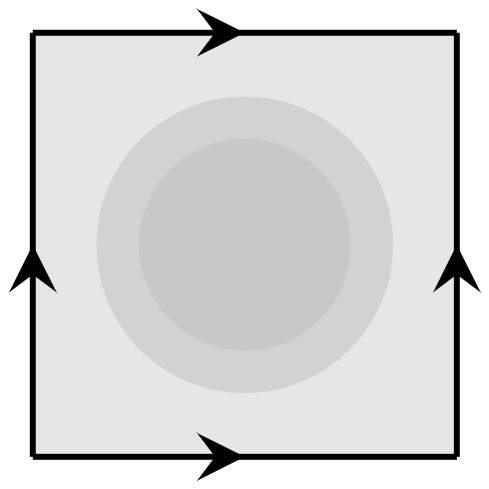
1) Io penso che mi chieda di utilizzare il teorema di Seifer van Kampen. Allora ragionando sul toro non riesco proprio a trovare sti aperti, ma ragionando sul poligono regolare \(P \) a quattro lati, i cui lati sono identificati dalla parola \(aba^{-1}b^{-1} \) che è omeomorfo al toro tramite quoziente che identifica i lati (quindi penso vada bene perché poi passo al quoziente (ma non so se poi mi cambia il gruppo fondamentale).
Pertanto se scelgo un punto \( p \in P \) nel interno del mio poligono \( P \), lo fisso e prendo come primo aperto \( A:= P \setminus \{ p \} \) e come secondo aperto prendo \(B \) essere un piccolo disco aperto attorno a \( p \). Ho che \( B \) è contrattibile e dunque \(B\) ha lo stesso tipo di omotopia di un punto, ovvero \( B \simeq \star \). \( A \cap B = B \setminus \{ p \} \) posso, tramite retrazione per deformazione, deformarlo continuamente ad un cerchio \( S^1 \) e dunque \( A \cap B \simeq S^1 \). Per quanto riguarda \( P \setminus \{p \} \) direi che posso deformarlo tramite retrazione per deformazione al bordo di \( P \), dunque quando passa al quoziente abbiamo che è omotopo a \( S^1 \vee S^1 \)
ma non sono sicuro se il tipo di omotopia di \( P \setminus \{p \} \) è quello di \( S^1 \) o quello di \( S^1 \vee S^1 \).
2) Ora abbiamo che \( \pi_1 B \cong \pi_1 \{ \star \} = \mathbf{1} \) il gruppo triviale, \( \pi_1 (A \cap B ) \cong \pi_1 S^1 = \mathbb{Z} \) e per finire abbiamo che \( \pi_1 A \cong \pi_1 ( S^1 \vee S^1 ) \) ed essendo spazi ben puntati abbiamo che
\[ \pi_1 A \cong \pi_1( S^1 \vee S^1 ) \cong \pi_1 S^1 \ast \pi_1 S^1 \cong \mathbb{Z} \ast \mathbb{Z} \cong F(x,y) \]
dove \( F(x,y) \) denota il gruppo libero a due generatori.
3) Usando Seifert van Kampen dovrei ottenere che
\[ \pi_1 T^2 = \pi_1 A \ast_{\pi_1 ( A \cap B)} \pi_1 B \cong F(x,y) \ast_{\mathbb{Z} } \mathbf{1} = F(x,y) \ast \mathbf{1} / N \]
dove \( N \) è il sottogruppo normale generato dal pushout dei gruppi. Quindi devo identificare le mappe \( \alpha \) e \( \beta \).
![\xymatrix{
\pi_1 ( A \cap B) \ar[r]^{\alpha}\ar[d]_{\beta} &\pi_1 B \\
\pi_1 A &
}](/forum/latexrender/pictures/6aaabb2bb0f059a70dcfe6c93a90194a.png "\xymatrix{
\pi_1 ( A \cap B) \ar[r]^{\alpha}\ar[d]_{\beta} &\pi_1 B \\
\pi_1 A &
}")
Per poter passare a cercare il pushout dei gruppi seguenti
![\xymatrix{
\mathbb{Z} \ar[r]^{\alpha_*}\ar[d]_{\beta_*} & \mathbf{1} \\
F(x,y) &
}](/forum/latexrender/pictures/fc6081bb56b99dbc6357e429f91f5a0a.png "\xymatrix{
\mathbb{Z} \ar[r]^{\alpha_*}\ar[d]_{\beta_*} & \mathbf{1} \\
F(x,y) &
}")
dove \( \alpha_* \) e \( \beta_* \) sono le mappe indotte dalle mappe \( \alpha \) e \( \beta \).
Allora direi che \( \beta \) e \( \beta_* \) sono banali, non abbiamo scelte infatti.
Mentre sapendo a priori che il gruppo fondamentale del toro è il gruppo abeliano libero a due generatori direi che \( N= \{ [a,b] \} \) dove con \( [a,b] \) intendo il commutatore e dunque
![\xymatrix{
\mathbb{Z} \ar[d] \ar[r]^{\alpha_*} \ar[d]_{\beta_*} & \mathbf{1} \ar[d] &\\
F(x,y) \ar[r]& F_{ab}(x,y) &
}](/forum/latexrender/pictures/8eacbd7aeb9faa276230d885aec8e1a7.png "\xymatrix{
\mathbb{Z} \ar[d] \ar[r]^{\alpha_*} \ar[d]_{\beta_*} & \mathbf{1} \ar[d] &\\
F(x,y) \ar[r]& F_{ab}(x,y) &
}")
Infatti \[ F(x,y) / N = \left< x,y | \right> / \{ [x,y]=1 \} = \left< x,y | xyx^{-1}y^{-1} \right> = F_{\operatorname{ab}}(x,y)\]
Vedo che ha senso che la mappa sia quello perché fondamentalmente il bordo del quadrato con cui identifico il toro è proprio la parola commutatore ma non saprei come trovare questa applicazione per davvero, nel senso che se a priori non avessi saputo il gruppo fondamentale del toro non ci sarei mai arrivato a trovare \( N \). Chi è \( \alpha \)? Chi è \( \alpha_* \) ?
)