Mi dite se la dimostrazione che ho fatto del teorema fondamentale ( dell'algebra lineare ) è corretta o se ci sono errori ?
Allego una img:
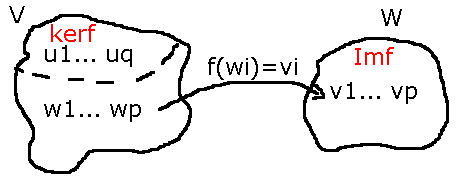
Considerata un'applicazione f: V -> W con V e W di dimensione finita, bisogna dimostrare che dim(kerf) + dim(imf) = dimV.
Se kerf=(0) o kerf=V la tesi si dimostra facilmente.
Consideriamo, per gli altri casi, che:
<b>{u1... uq} è una base di Kerf in V con 0 < q < n
{v1... vp} è una base di Imf in W</b>
Bisogna vedere che p + q = n con un semplice calcolo delle dimensioni.
Siccome v1... vp appartengono a Img in W esisteranno p vettori in V che non fanno parte di Kerf tali che f(wi) = vi.
Quindi basta dimostrare che in V, i q vettori di kerf e i p vettori di V formano una base, cioè {u1... uq, w1... wp} è una base di V di dimensione p + q.
Bisogna dimostrare che tali vettori sono generatori e che sono linearmente indipendenti.
Per dimostrare che sono generatori si può considerare un vettore x di V tale che f(x) appartiene all'imf=L(v1...vp).
Se f(x) appartiene all'immagine allora si potrà scrivere come combinazioni lineare dei vettori che la generano, quindi:
f(x) = a1v1+... + apvp = f(a1w1+... +apwp);
Dato che x appartiene anche a v potrà essere scritto anche come combinazioni lineare dei vettori che formano kerf, si ha quindi:
x = a1w1+... +apwp + b1u1+... +bpuq.
Il che verifica il fatto che siano generatori.
Per l'indipendenza deve essere:
a1u1+... +aquq + b1w1+... +bpwp =0.
Applicando la f ai vettori di kerf ed i restanti, si ha:
a1f(u1)+... +aqf(uq) + b1f(w1)+... +bpf(wp) =0;
Ora f(ui) = 0 e siccome f(wi) = vi e vi sono tutti vettori indipendenti perchè formano una base di W allora si conclude che sono indipendenti... anche perchè {u1... uq} formano una base di Kerf quindi devono essere indipendenti anche loro.
La relazione è verificata se e solo se tutti i coefficienti sono nulli.
Va bene come l'ho dimostrata ?
Non mi convince molto la dimostrazione dell'indipendenza e dei generatori... sul libro era sottointesa più o meno e quindi ho provato a farla da me... ma sta bene ?
Mi spiegate come posso fare a dire che x si scrive come combinazione lineare dei vettori di kerf e di wi ?
E per l'indipendenza ? sta bene dire che f(u) = 0 ???
Grazie a tutti!
