Si consideri il seguente integrale:
\(\displaystyle I = \iint_{D} |\cos(x+y)| dxdy \)
da risolvere sul dominio:
\(\displaystyle D = \{(x,y) \in \mathbb{R}^{2} : 0 \leq x\leq \pi, 0\leq y \leq \pi\}. \)
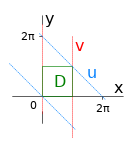
Per semplificare l'integranda, ho considerato la trasformazione:
\(\displaystyle \left\{\begin{matrix}
u = x+y \\
v = x
\end{matrix}\right. \)
il cui determinante Jacobiano in modulo risulta di valore unitario.
Dalle informazioni del dominio, ricavo che \(\displaystyle 0\leq x+y \leq 2\pi \), quindi il nuovo dominio risulta essere:
\(\displaystyle D^{'} = \{(v,u) \in \mathbb{R}^{2} : 0 \leq v\leq \pi, 0\leq u \leq 2\pi\} \).
Impostando finalmente il nuovo integrale, risulta:
\(\displaystyle I = \int_{0}^{\pi} dv \int_{0}^{2\pi} |\cos (u)| du = \pi\int_{0}^{2\pi} |\cos (u)| du \)
L'integrale del coseno si svolge semplicemente spezzando l'intervallo di integrazione, in modo tale da togliere il valore assoluto. Il risultato che ottengo è $4\pi$, quando in realtà dovrebbe risultare $2\pi$.
Quali sono gli errori in questo procedimento? Vi ringrazio.
10 messaggi
• Pagina 1 di 1
Calcolo integrale doppio con cambiamento di variabili
"È la somma che fa il totale!"
(Antonio Griffo Focas Flavio Angelo Ducas Comneno Porfirogenito Gagliardi de Curtis di Bisanzio)
(Antonio Griffo Focas Flavio Angelo Ducas Comneno Porfirogenito Gagliardi de Curtis di Bisanzio)
-

CosenTheta - Average Member

- Messaggio: 8 di 601
- Iscritto il: 02/09/2019, 22:18
Re: Calcolo integrale doppio con cambiamento di variabili
CosenTheta ha scritto:... Quali sono gli errori in questo procedimento? ...
Direi nella trasformazione (non corrispondenza) del dominio.
"Il circuito ha sempre ragione" (Luigi Malesani)
- RenzoDF
- Cannot live without

- Messaggio: 5505 di 15474
- Iscritto il: 06/08/2014, 09:08
Re: Calcolo integrale doppio con cambiamento di variabili
CosenTheta ha scritto:\(\displaystyle D^{'} = \{(v,u) \in \mathbb{R}^{2} : 0 \leq v\leq \pi, 0\leq u \leq 2\pi\} \).
Non è \(\displaystyle D^{'} = \{(v,u) \in \mathbb{R}^{2} : 0 \leq v\leq \pi, 0\leq u-v \leq \pi\} \) ?
Ultima modifica di DeltaEpsilon il 07/09/2019, 23:00, modificato 1 volta in totale.
É così dichiarato che è celato! Non c'è nulla di più sfuggente dell'ovvio. (Sherlock Holmes)
-
DeltaEpsilon - Average Member

- Messaggio: 28 di 648
- Iscritto il: 08/04/2019, 18:58
Re: Calcolo integrale doppio con cambiamento di variabili
RenzoDF ha scritto: Direi nella trasformazione (non corrispondenza) del dominio.
Potresti mostrarmi come lo scriveresti?
"È la somma che fa il totale!"
(Antonio Griffo Focas Flavio Angelo Ducas Comneno Porfirogenito Gagliardi de Curtis di Bisanzio)
(Antonio Griffo Focas Flavio Angelo Ducas Comneno Porfirogenito Gagliardi de Curtis di Bisanzio)
-

CosenTheta - Average Member

- Messaggio: 9 di 601
- Iscritto il: 02/09/2019, 22:18
Re: Calcolo integrale doppio con cambiamento di variabili
Più che scriverlo, direi che posso rappresentare la non corrispondenza in forma grafica
Ultima modifica di RenzoDF il 08/09/2019, 14:01, modificato 1 volta in totale.
"Il circuito ha sempre ragione" (Luigi Malesani)
- RenzoDF
- Cannot live without

- Messaggio: 5506 di 15474
- Iscritto il: 06/08/2014, 09:08
Re: Calcolo integrale doppio con cambiamento di variabili
L'unica cosa che mi viene in mente è riscrivere $D^{'}$ in questo modo:
$D′={(v,u)∈R^{2}:0≤v≤π,v≤u≤v+\pi}$
$D′={(v,u)∈R^{2}:0≤v≤π,v≤u≤v+\pi}$
"È la somma che fa il totale!"
(Antonio Griffo Focas Flavio Angelo Ducas Comneno Porfirogenito Gagliardi de Curtis di Bisanzio)
(Antonio Griffo Focas Flavio Angelo Ducas Comneno Porfirogenito Gagliardi de Curtis di Bisanzio)
-

CosenTheta - Average Member

- Messaggio: 10 di 601
- Iscritto il: 02/09/2019, 22:18
Re: Calcolo integrale doppio con cambiamento di variabili
Esatto 
Le rette: superiore $y=\pi$ e inferiore $y=0$, del dominio $D$ portano rispettivamente a
$u=v+\pi$ e $u=v$,
mentre ovviamente, per le due verticali $v=0$ e $v=\pi$.

Le rette: superiore $y=\pi$ e inferiore $y=0$, del dominio $D$ portano rispettivamente a
$u=v+\pi$ e $u=v$,
mentre ovviamente, per le due verticali $v=0$ e $v=\pi$.
"Il circuito ha sempre ragione" (Luigi Malesani)
- RenzoDF
- Cannot live without

- Messaggio: 5507 di 15474
- Iscritto il: 06/08/2014, 09:08
Re: Calcolo integrale doppio con cambiamento di variabili
A questo punto, impostando nuovamente l'integrale su questo dominio, ottengo:
\(\displaystyle \int_{0}^{\pi} dv \int_{v}^{v + \pi} |\cos(u)|du\)
ma avendo la variabile $\u$ che non varia più tra due costanti, ma tra $v$ e $v+\pi$, come discuto
il modulo per poterlo togliere?
\(\displaystyle \int_{0}^{\pi} dv \int_{v}^{v + \pi} |\cos(u)|du\)
ma avendo la variabile $\u$ che non varia più tra due costanti, ma tra $v$ e $v+\pi$, come discuto
il modulo per poterlo togliere?
"È la somma che fa il totale!"
(Antonio Griffo Focas Flavio Angelo Ducas Comneno Porfirogenito Gagliardi de Curtis di Bisanzio)
(Antonio Griffo Focas Flavio Angelo Ducas Comneno Porfirogenito Gagliardi de Curtis di Bisanzio)
-

CosenTheta - Average Member

- Messaggio: 11 di 601
- Iscritto il: 02/09/2019, 22:18
Re: Calcolo integrale doppio con cambiamento di variabili
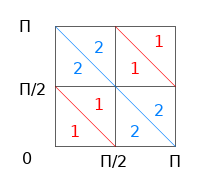
Hai ragione, possiamo suddividere quel dominio in otto parti
suddivisione che, grazie alla periodicità della funzione integranda, permetterà di determinare l'integrale cercato I, a partire dai due integrali elementari I1 e I2, via $I=4(I_1+I_2)$, dove:
$I_1=\int_{0}^{\pi/2}\text{d}v\int_{v}^{\pi/2} \ \cos u \ \text{d}u$
e
$I_2=\int_{\pi/2}^{\pi }\text{d}v\int_{v}^{\pi } -\cos u \ \text{d}u$.
suddivisione che, grazie alla periodicità della funzione integranda, permetterà di determinare l'integrale cercato I, a partire dai due integrali elementari I1 e I2, via $I=4(I_1+I_2)$, dove:
$I_1=\int_{0}^{\pi/2}\text{d}v\int_{v}^{\pi/2} \ \cos u \ \text{d}u$
e
$I_2=\int_{\pi/2}^{\pi }\text{d}v\int_{v}^{\pi } -\cos u \ \text{d}u$.
"Il circuito ha sempre ragione" (Luigi Malesani)
- RenzoDF
- Cannot live without

- Messaggio: 5510 di 15474
- Iscritto il: 06/08/2014, 09:08
Re: Calcolo integrale doppio con cambiamento di variabili
Grazie mille per l'aiuto.
"È la somma che fa il totale!"
(Antonio Griffo Focas Flavio Angelo Ducas Comneno Porfirogenito Gagliardi de Curtis di Bisanzio)
(Antonio Griffo Focas Flavio Angelo Ducas Comneno Porfirogenito Gagliardi de Curtis di Bisanzio)
-

CosenTheta - Average Member

- Messaggio: 12 di 601
- Iscritto il: 02/09/2019, 22:18
10 messaggi
• Pagina 1 di 1
Chi c’è in linea
Visitano il forum: Nessuno e 1 ospite