Un pentagono ...

[Erasmus_First]

I 5 punti $A$, $B$, $C$, $D$ ed $E$ distano tutti $r$ dal punto $O$ e
AB = BC = CD = 2 u;
DE = EA = 3 u.
Quanti u vale $r$?
:
______

[orsoulx]

Testo nascosto, fai click qui per vederlo

Le diagonali $BE$ e $ CE $ misurano $ 4u $ e $ r=8/sqrt(15)u$

Ciao

[bub]

Simpatico il problema. Questo però era un caso particolare.
In generale se si ha una ennupla finita di lunghezze, come si fa a determinare la lunghezza del raggio della circonferenza che circoscrive il poligono inscrivibile in un cerchio formato da segmenti di queste lunghezze?
C'è qualche formula generale?
Quando sono uguali il problema si riduce a trovare il raggio del cerchio che circoscrive il poligono regolare...

$r = l/(2*sin(pi/n))$

Se l'ennupla è di tre elementi $[a, b ,c]$ si può usare la formula

$r = (a * b * c) / sqrt((a + b + c)*(-a + b + c)*(a - b + c)*(a + b - c))$

ma se non si verificano i due casi precedenti? Che sistema o formula si può usare?

Ovviamente bisogna prendere le sequenze con le quali si può costruire un poligono inscrivibile.

[Erasmus_First]

Testo nascosto, fai click qui per vederlo

Le diagonali $BE$ e $ CE $ misurano $ 4u $ e $ r=8/sqrt(15)u$

Ciao

[Dicci però come hai risolto il quiz.]
____

[Erasmus_First]

[...] C'è qualche formula generale?
Quando sono uguali il problema si riduce a trovare il raggio del cerchio che circoscrive il poligono regolare...
$r = l/(2*sin(pi/n))$
Ma se son diversi? Che formula si può usare?

Testo nascosto, fai click qui per vederlo

Prima di risolvere il problema di questo quiz [con una equazione algebrica col metodo che esporrò tra poco] il problema l'avevo risolto con la calcolatrice grafica (cioè con l'applicazione "Grapher" per Apple) impostando un'equazione trascendente facile-facile – facile da impostare! – che cocettualmente può essere risolta con qualche metodo per approssimazioni successive (per esempio con metodo dicotomico). Questa equazione va bene con qualsiasi numero n di lati di lunghezza qualsiasi.
[Stiamo parlando di un poligono convesso irregolare circoscrittibile].
La somma degli angoli al centro (ossia degli angoli al vertice degli n triangoli isosceli con un lato del poligono per base e due raggi [del cerchio circoscritto] per i lati uguali) è un angolo giro. La somma delle metà di questi angoli è un angolo piatto. La metà dell' angolo al centro del lato k-esimo di lunghezza $l_k$ (con k da 1 a n) è $arcsin(l_k/(2r))$.
L'equazione trascentente è pertanto:
$sum_{k=1}^{n}arcsin(l_k/(2r)) = π$
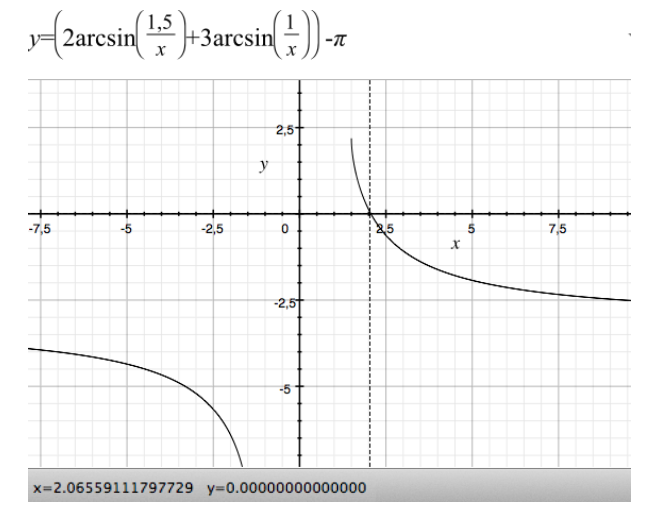
Guarda questa figura (che ho preso direttamente dallo schermo preparando questo quiz del pentagono.
NB: "Grapher vuole per incognita la lettera x, che qui è proprio la cercata lunghezza r del raggio del cerchio circoscritto.

Dall'equazione trascendente, uguagliando a zero il secondo membro della equazione che sta in testa alla figura] e ponendo:
$α =arcsin(1/r)$ e $β = arcsin((1,5)/r)$
si passa all'equazione trigonometrica
$sin(3α+2β) = sin(π) = 0$ ⇔ $sin(3α)cos(2β)+cos(3α)sin(2β) = 0$
dalla quale, usando le uguaglianze:
$sin(3φ) = –4sin^3(φ) + 3sin(φ); sin(2 φ)=2sin(φ)cos(φ) = 2sin(φ)sqrt(1-sin^2(φ))$;
$cos(3φ) = 4cos^3(φ) - 3cos(α) = [1–4sin^2(φ)]sqrt(1-sin^2(φ)); cos(2 φ)=1-2sin^2(φ)$
si ricava l'equazione nelle incognite $sin(α)$ e $sin(β)$:
$[-4sin^3(α)+3sin(α]·[1-2sin^2(β)] + [1–4sin^2(α)]sqrt(1-sin^2(α))]·2[sin(β)sqrt(1-sin^2(β))]$.
Per comodità metto $sin(α) = x = 1/r$ e mi ricordo che è $sin(β) = 3/2·1/r = 3/2sin(α) = 3/2x$.
Ottengo così l'equazione in x:
$[-4x^3 + 3x]{1-9/2x^2]+[(1-4x^2)sqrt(1-x^2)]·3xsqrt(1-9/4x^2)$.
Da questa, razionalizzando e poi semplificando (dovendo anche essere $x ≠ 0$) ho successivamente:
$(3x-ax^3)(2-9x^2)+ [(1-4x^2)sqrt(1-x^2)]·3xsqrt(4-9x^2)$ ⇔
⇔ $6-35x^2+36x^4 =(12x^2-3)sqrt(4-13x^2+9x^4)$ ⇒
⇒ $(6-35x^2+36x^4)^2 = (12x^2-3)^2(4-13x^2+9x^4)$ ⇔
⇔ 36-420x^2+1657x^4-2520x^6+1296x^8 = (9-72x^2+144x^4)(4-13x^2+9x^4)$ ⇔
⇔ 36-420x^2+1657x^4-2520x^6+1296x^8 =$
$= 36-405x^2+1593x^4-259x^6+1296x^8$ ⇒
⇒$15-64x^2=0$ ⇔ $x^2 = 15/64$ ⇒ $x = sqrt15/8$ ⇔ $r = 8/sqrt15 = 2,06559111797729$.
Il caso di questo quiz è molto semplice. Tuttavia il metodo impiegato concettualmente va sempre bene perché ogni $sin(α_k) = l_k/(2r)$ (con k da 1 a n ) è proporzionale ad $l_k$ e quin di si può assumere una sola incognita (diciamola $x = sin(α_h)$ e scrivere tutti i $sin(α_k)$ come $l_k/l_hsin(α_h) = l_k/l_hx$.
Naturalmente quanto più numerose sono le diversità dei lati dell'n-agono tanto più laboriosa è la razionalizzazione e maggiore il grado finale dell'equazione algebrica. Se poi il grado dell'equazione alla fine risulta maggiore di 4 non è nemmeno possibile risolvere l'equazione per radicali!! Allora – dati i moderni mezzi di calcolo – tanto vale risolvere con metodi iterativi di successive migliori approssimazioni l'equazione iniziale (che riperto):
$sum_{k=1}^{n}arcsin(l_k/(2r))–π =0$.

________

[giammaria]

@orsoulx. Come sei arrivato alla soluzione? Suppongo con un bel ragionamento, che vorrei conoscere.
Io ho risolto in modo molto banale.

Testo nascosto, fai click qui per vederlo

Indicando con $2x, 2y$ gli angoli al centro ho
$3*2x+2*2y=360°-> y=90°-(3x)/2$
Essendo $x,y$ positivi, l'ultima formula dice anche che $x/2<30°$ e quindi ha seno e coseno positivi. Per il teorema della corda
${(2rsinx=2u),(2rsiny=3u):}->{(rsinx=u),(2rcos frac(3x)2=3u):}$
Posto per brevità $z=cos frac x 2$ ed usando le formule di duplicazione e triplicazione ottengo
${(2rzsqrt(1-z^2)=u),(2rz(4z^2-3)=3u):}$
ed il prodotto incrociato porge
$2ruz*3sqrt(1-z^2)=2ruz*(4z^2-3)$
Semplifico ed elevo a quadrato, arrivando a
$16z^4-15z^2=0->16z^2=15->z=sqrt15/4$
Basta ora sostituire in una delle equazioni del sistema per ottenere $r=8/sqrt15 u$

[orsoulx]

Veramente, ho risolto il problema, senza carta e matita, mentre guardavo una partita di pallavolo:

Testo nascosto, fai click qui per vederlo

per abitudine affronto i problemi di geometria cercando simmetrie. Il pentagono è simmetrico rispetto alla mediana (altezza bisettrice, asse) del triangolo isoscele $ BEC$ e, scambiando le posizioni dei lati $ CD $ e $DE $, ottengo un trapezio isoscele $ EBCD' $ di base minore $ CD'=3 $, lati obliqui $ BC=ED'=2 $ e base maggiore $ EB $ congruente alle diagonali. Trapezio che posso spezzare in $ EB'CD' $ (parallelogramma di lati $ 2 $ e $ 3 $ ) e $ B'BC$ triangolo isoscele simile, per avere l'angolo alla base in comune, a $ BEC $. Similitudine che porge il prodotto base maggiore per differenza basi uguale a $ 4 $, mentre la loro differenza è $ 3 $. Dunque $ B'B =1$ e $EB=EC=4 $.
L'altezza del triangolo $ BEC$ è allora $ EH = sqrt{4^2-1^2)=sqrt(15) $ e la similitudine fra $BEH $ e $EMO$ (con $ M $ punto medio di $ EB $ e $ O $ centro della circonferenza circoscritta di raggio $OE$) porta al risultato finale $ r=(2 cdot 4)/sqrt(15) $.

@Erasmus:
Continui a non usare lo spoiler per i tuoi interventi. Mi pare che la tua risposta a bub sia corretta solo quando il centro della circonferenza circoscritta è interno al poligono: quando è esterno occorre una piccola modifica.
Ciao

[bub]

Ciao Erasmus, ma in pratica si può sempre tirare fuori un'equazione polinomiale in una incognita?
Speravo ci fosse una relazione più compatta. Ho trovato in rete anche la formula per 4 lunghezze $[a, b, c, d]$...

$r = sqrt(((a*b + c*d)*(a*c + b*d)*(a*d + b*c))/((-a+b+c+d)*(a-b+c+d)*(a+b-c+d)*(a+b+c-d)))$

Grazie comunque, più o meno ho afferrato la cosa.

Rimane bloccata anche l'area di questi poligoni mi sembra, in linea di principio questa si potrebbe calcolare in funzione della lunghezza dei lati.

Se cade fuori il centro della circonferenza forse l'arcoseno corrispondente al "lato base" del poligono deve finire all'altro membro dell'equazione con la sommatoria (o lasciarlo dalla stessa parte col segno meno), però non so magari dico stupidaggini.

[orsoulx]

Se cade fuori il centro della circonferenza forse l'arcoseno corrispondente al "lato base" del poligono deve finire all'altro membro dell'equazione...

Giusto (a patto di eliminare $ \pi $). Il "lato base" è quello di maggior lunghezza.
Ciao

[giammaria]

Grazie, orsoulx; è veramente una bella soluzione.