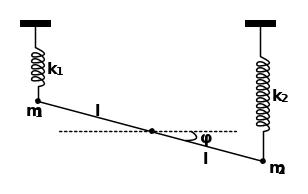
Dove le due molle sono a riposo quando l'asta è orizzontale.
Ho provato a risolverlo con metodi energetici:
L'energia cinetica del sistema è
$$ T = \frac{1}{2} (m_1 + m_2) l^2 \dot{ \varphi} ^2 $$
mentre l'energia potenziale
$$ V = \frac{1}{2} (k_1 + k_2) l^2 \cos^2 \varphi $$
quindi la lagrangiana per piccole oscillazioni, espandendo il coseno al secondo termine, è
$$ L = T-V = \frac{1}{2} (m_1 + m_2) l^2 \dot{ \varphi} ^2 - \frac{1}{2} (k_1 + k_2) l^2 \left (1+\frac{\varphi^2}{2} \right )^2 $$
computando l'equazione di Eulero-Lagrange ottengo
$$\frac{\mathrm{d} }{\mathrm{d} t} \frac{\partial L}{\partial \dot{\varphi}}-\frac{\partial L}{\partial \varphi}=(m_1+m_2) l^2 \ddot{\varphi} +(k_1+k_2) l^2 \varphi=0$$
purtroppo questa equazione non è corretta.
La soluzione proposta dal mio professore è
$$(m_1+m_2) l^2 \ddot{\varphi} +2(k_1+k_2) l^2 \varphi=0$$
ma io non riesco proprio a capire da dove salti fuori quel due al secondo termine. Evidentemente non sto considerando qualcosa nella scrittura dell'energia potenziale.
Grazie a tutti coloro che hanno avuto la pazienza di arrivar si qui. Sapreste spiegarmi qual'è la causa di tale temine?