luogo geometrico dei punti medi di una circonferenza

[rosa munda]

Buongiorno. Sono alle prese con un problema interessante, ma che sono incapace di risolvere. Mi dareste un suggerimento per avvicinarmi alla soluzione? Ecco il problema:

Trovare il luogo geometrico dei punti medi delle corde della circonferenza $x^2+y^2-4y-4=0$ sapendo che le rette contenenti tali corde passano per l'origine delle coordinate. (risultato : $x^2+y^2-2y =0$ ).

Ho ragionato in questo modo:
-) le rette secanti passano per 0 , allora sono del tipo $y=mx$
-) le rette secanti devono avere $ Delta>0 $
-) punti medi allora le coordinate delle rette devono avere $ Y = (y1+y2) / 2$ E $ X = ( x1+x2 )/ 2 $

(digressione : come faccio a fare il pedice alle y1 - y2 etc. ?)

Ho messo in sistema la circonferenza data con la retta generica y=mx - volendo trovare m - ma il discriminante è un numero (8), quindi ovviamente le rette valgono per ogni m (intuibile forse, no?).

Devo forse considerare una retta Y = m X (cioè con i punti medi sopra indicati) e sostituirla nella funzione della circonferenza? Ma mi resta il c (cioè -4).

E qui finisce il mio ragionamento.
Vi ringrazio anticipatamente e vi auguro buona giornata.

[gugo82]

Hai il sistema:
\[
\begin{cases}
x^2 + y^2 - 4 y -4 =0\\
y=mx
\end{cases}
\]
il quale ha due soluzioni distinte per ogni valore di $m$ (per ovvi motivi geometrici... Fai un disegno!).
Tali soluzioni le puoi calcolare esplicitamente, ma ciò è abbastanza inutile per quel che devi fare.
Infatti, se ricordi bene, in un'equaizone di secondo grado con due radici reali, la quantità $x_1+x_2$ è sempre uguale all'opposto del coefficiente del termine in $x$ diviso per il coefficiente di $x^2$, cioè vale:
\[
x_1, x_2 \text{ risolvono } ax^2+bx +c =0\quad \Rightarrow \quad x_1+x_2 = -\frac{b}{a}\; ;
\]
dunque, detti \(a(m)\) e \(b(m)\) i coefficienti della risolvente quadratica in $x$ del tuo sistema ed $x_1(m), x_2(m)$ le sue soluzioni ed $y_1(m),y_2(m)$ le soluzioni ad esse associate dalla seconda equazione, hai certamente:
\[
\begin{split}
\frac{x_1(m) + x_2(m)}{2} &= - \frac{b(m)}{2a(m)}\\
\frac{y_1(m) + y_2(m)}{2} &= \frac{mx_1(m) + mx_2(m)}{2}\\
&=- \frac{m\ b(m)}{2a(m)}\; .
\end{split}
\]
Conseguentemente le coordinate \((x(m), y(m))\) dei punti medi dei segmenti \((x_1(m),y_1(m))\) ed \((x_2(m), y_2(m))\) sono date da:
\[
\begin{cases}
x(m) = - \frac{b(m)}{2a(m)}\\
y(m) =-m \frac{b(m)}{2a(m)}\; .
\end{cases}
\]
L'equazione del luogo geometrico si ottiene dal sistema:
\[
\begin{cases}
x = - \frac{b(m)}{2a(m)}\\
y =-m \frac{b(m)}{2a(m)}
\end{cases}
\]
cercando di eliminare il parametro $m$.

[rosa munda]

Grazie moltissimo per la risposta come sempre molto sollecita. Ora devo studiarla e comprenderla per bene ma lo potrò fare solo domattina. Per ora grazie di nuovo e buonissima serata.

[teorema55]

Per usare meno calcoli:

La circonferenza

$x^2+y^2-4y-4=0$

ha il centro in

$C(0,2)$

e interseca l'asse x nei punti

$I_1(-2,0)$

e

$I_2(2,0)$

Prendiamo due di tutte le rette del tipo

$y=mx$

la

$x=0$

cioè l'asse y (è una retta limite, che fa parte della famiglia suddetta se $m=∞$, e la

$y=0$ per $m=0$

cioè l'asse x.

Puoi verificare che entrambe sono secanti la circonferenza. La prima, cioè l'asse y, interseca la circonferenza lungo il diametro verticale, quindi il suo punto medio è il centro della circonferenza

$C(0,2)$

La seconda, l'asse x, la interseca nei punti

$I_1$ e $I_2$

e il suo punto medio è l'origine degli assi.

Per ragioni di simmetria, il luogo che cerchi è la circonferenza di centro

$C_1(0,1)$

e raggio

$R_1=1$

la cui equazione sei in grado di scrivere.

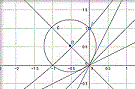
Allego una immagine di una retta secante con

$m=1$

cioè la bisettrice del 1° e 3° quadrante, la

$y=x$

Come vedi il punto medio della corda individuata è

$M(1,1)$

che, ovviamente, appartiene sia alla retta che alla circonferenza luogo geometrico dei punti medi delle corde.

[mgrau]

Con un po' di logica e per usare meno calcoli:
.
.
.

Per ragioni di simmetria, il luogo che cerchi è la circonferenza ....

Vuoi dire che dalla sola simmetria ricavi che il luogo cercato è una circonferenza?

[teorema55]

No, ma è un ottimo punto di partenza per orientarsi................e comunque, anche sì, usando un po' di logica e di buon senso. O forse ho sbagliato?

[mgrau]

Magari sì, ma non ci arrivo

[teorema55]

Magari no.

[orsoulx]

Non mi pare che usando la geometria analitica i calcoli necessari siano molto complicati. Però la dimostrazione con la sola geometria euclidea è semplicissimo. Se $ O $ è il centro della circonferenza e $ P $ un punto qualsiasi del cerchio (distinto da $ O $ se si vuole evitare il caso degenere), il punto medio di una corda qualsiasi passante per $P $ 'vede' il segmento $ OP $ sotto un angolo retto, e allora il luogo cercato è la circonferenza di diametro $ OP $.
Ciao

[teorema55]

E, se proprio qualcuno è scettico, lo può vedere qui:

https://www.geogebra.org/m/R4EKhgzG