Esercizio su densità di probabilità

[marcobj99]

Si consideri la densità di probabilità
$ f(t) = 3/4 * [1−(t + 1−θ)^2]I(θ−2,θ)(t) $, dove θ è un numero reale incognito.
(a) Si disegni il grafico di f.
(b) Si calcoli il valore atteso µ e la varianza σ2 di una variabile aleatoria con densità f. [µ = θ−1, σ2 = 1/5].
Buonasera, ho difficoltà coi punti di quest'esercizio.
Il primo, non capisco come disegnare quella funzione se theta è incognito.
Il secondo, so che va fatto con l'integrale di x*f(x) nel primo caso e con quello di x^2*f(x) meno quello precedentemente calcolato per la varianza, ma ho difficoltà coi calcoli

[tommik]

@marcobj99: hai 56 messaggi, mi pare il caso di usare le formule in modo corretto....tutte le formule, non solo la prima.

L'esercizio si risolve tutto in modo immediato e senza noiosi calcoli, però è un esercizio molto ben scritto che ti obbliga a ragionare oppure a perderti in un ammasso informe di calcoli (complimenti al prof )

a) riscrivi la densità in questo modo:

$f_T(t)=3/4{-t^2+2(theta-1)t+[1-(theta-1)^2]}mathbb{1}_((theta-2;theta))(t)$

...ora dovrebbe essere evidente quale sia la sua rappresentazione grafica: una parabola¹ troncata sul dominio specificato, con i rami rivolti verso il basso e con vertice di ascissa $-b/(2a) = -(2(theta-1))/(-2)=theta-1$....ops abbiamo già calcolato anche la media² richiesta al punto b)

b)

Prima osservazione

Il secondo, so che va fatto con l'integrale di x*f(x) nel primo caso e con quello di x^2*f(x) meno quello precedentemente calcolato per la varianza, ma ho difficoltà coi calcoli

....meno quello precedentemente calcolato "al quadrato"

$V[X]=mathbb{E}[X^2]-mathbb{E}^2[X]$

Seconda osservazione
Per il calcolo della varianza, con un semplice cambio di variabile, ottieni

$V[T]=3/4int_(-1)^(1)[y^2-y^4]dy=3/4[y^3/3-y^5/5]_(-1)^(1)=3/4[2/3-2/5]=1/5$

EDIT:

Testo nascosto, fai click qui per vederlo

provo a spiegarmi meglio.

Iniziando a calcolare la varianza della tua variabile utilizzando la definizione che conosci, subito ti accorgi che i calcoli da fare diventano parecchio lunghi a causa di questo parametro che ci disturba. Allora la prima cosa che farei io è quella di ragionare qualche minuto e vedere se è possibile semplificare in qualche modo i lunghi e noiosi calcoli da fare.

Partiamo quindi dalla rappresentazione grafica della tua densità (che ti ho già spiegato prima e che comunque, guarda caso, era richiesta al primo punto dell'esercizio):

(cliccami per ingrandirmi)


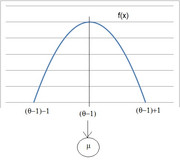
Ora domandati....ma se spostiamo $theta$ di qua o di là sull'asse reale cosa cambierà alla varianza della tua variabile? Ovvero: se sposti la tua parabola di qua o di là sull'asse reale cosa cambierà alla forma della distribuzione? non cambierà proprio nulla...tieni presente che la varianza è una misura media di distanza fra i valori della variabile rispetto alla loro media. In altri termini, la varianza in questo caso è indipendente dal parametro. Allora ti fissi un valore opportuno del parametro (quello che ti è più comodo) e calcoli quanto ti viene la varianza. In particolare, se fissi $theta=1$ ottieni una variabile con la stessa varianza della tua variabile T ma molto più semplice da calcolare. Infatti, fissando $theta=1$ la media sarà zero, la densità sarà

$f(y)=3/4(1-y^2)mathbb{1}_((-1;1))(y)$

e la varianza sarà pari al momento secondo (essendo la media zero)

In definitiva

$V[Y]=mathbb{E}[Y^2]=3/4int_(-1)^(1)y^2(1-y^2)dy=1/5$

Un ragionamento un po' più raffinato (e che speravo riuscissi a fare da solo) è il seguente:

Assodato che la media della variabile di partenza è $mathbb{E}[T]=(theta-1)$ calcoliamo la seguente quantità pivotale

$Y=T-mu_T=T-(theta-1)$

di media zero e varianza $V[Y]=V[T]$ per note proprietà della varianza.

Ora non resta che calcolare la distribuzione della variabile trasformata tramite la formula

$f_(Y)(y)=f_T(g^(-1)(y))|d/(dy)g^(-1)(y)|$

che in pratica è semplicissimo data la linerarità della trasformazione. Infatti la derivata della funzione di trasformazione è 1 e quindi per calcolare la densità della nuova variabile basta sostituire $t=y+theta-1$ nella densità iniziale e proseguire come spiegato prima.


cordiali saluti

---

Note

1. ovvero è una funzione del tipo $y=ax^2+bx+c$ ↑
2. nel caso di distribuzione simmetrica ed unimodale infatti media moda e mediana coincidono ↑

[marcobj99]

Grazie mille, scusa se non ho usato il LaTex.

Comunque, non mi è chiaro come calcoli la varianza, e non capisco quale cambio di variabile utilizzi.