Ho questo problemino: generare tutti i sottoinsiemi di un insieme dato, ordinato per dimensione.
Per esempio: {}, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}.
Il problema in questo caso non è tanto l'implementazione dell'algoritmo, ma capire come ottenere l'algoritmo. Devo implementare qualcosa relativo al calcolo combinatorio per risolverlo?
Potreste darmi una pista su cui ragionare?
44 messaggi
• Vai alla pagina... • 1, 2, 3, 4, 5
Problema di combinatoria
Ultima modifica di ZfreS il 09/07/2019, 15:26, modificato 1 volta in totale.
- ZfreS
- Cannot live without

- Messaggio: 1761 di 4589
- Iscritto il: 22/10/2016, 17:52
Re: Problema di
Un generico sottoinsieme di un insieme dato è un insieme in cui ciascun elemento c'è oppure non c'è. Il numero di sottoinsiemi è quindi dato da tutte le combinazioni possibili di elementi che ci sono o non ci sono. Per esempio, se l'insieme di partenza è {1,2,3}, puoi vedere il sottoinsieme {1,2} come il numero binario 110, eccetera.
Spero che l'indizio sia utile, ma non ne sono sicurissimo
Spero che l'indizio sia utile, ma non ne sono sicurissimo
Un matematico ha scritto:... come mia nonna che vuole da anni il sistema per vincere al lotto e crede che io, in quanto matematico, sia fallito perché non glielo trovo

-

Raptorista - Moderatore

- Messaggio: 5279 di 9616
- Iscritto il: 28/09/2008, 19:58
Re: Problema di combinatoria
La tua osservazione mi sembra corretta, ho avuto perciò un'idea basato su questo, ma penso che richieda una dimostrazione matematica. Supponiamo che l'insieme sia già ordinato: {1,2,3,4,5}. I sottoinsiemi sono:
{1,2} {2,3} {3,4} {4,5}
{1,3} {2,4} {3,5}
{1,4} {2,5}
{1,5}
In pratica ho notato questo ordine, poi ci sono da aggiungere tutti quelli con gli elementi singoli quindi: {1} {2} {3} {4} {5}
Aspetto la risposta di qualcuno esperto, ma intanto questa è una mia idea di partenza. Poi è da vedere il metodo che le ordina mentre crea i sottoinsiemi.
{1,2} {2,3} {3,4} {4,5}
{1,3} {2,4} {3,5}
{1,4} {2,5}
{1,5}
In pratica ho notato questo ordine, poi ci sono da aggiungere tutti quelli con gli elementi singoli quindi: {1} {2} {3} {4} {5}
Aspetto la risposta di qualcuno esperto, ma intanto questa è una mia idea di partenza. Poi è da vedere il metodo che le ordina mentre crea i sottoinsiemi.
- ZfreS
- Cannot live without

- Messaggio: 1762 di 4589
- Iscritto il: 22/10/2016, 17:52
Re: Problema di combinatoria
Quelli non sono tutti i sottoinsiemi però.
Dal punto di vista dell'implementazione, un approccio ricorsivo potrebbe funzionare se l'insieme non è gigantesco.
Dal punto di vista dell'implementazione, un approccio ricorsivo potrebbe funzionare se l'insieme non è gigantesco.
Un matematico ha scritto:... come mia nonna che vuole da anni il sistema per vincere al lotto e crede che io, in quanto matematico, sia fallito perché non glielo trovo

-

Raptorista - Moderatore

- Messaggio: 5280 di 9616
- Iscritto il: 28/09/2008, 19:58
Re: Problema di combinatoria
Non considero {1,2} e {2,1} come sottoinsiemi diversi. L'algoritmo deve prestarsi bene anche per insiemi di 50 elementi. Quindi penso che l'approccio ricorsivo non sia la miglior soluzione.
- ZfreS
- Cannot live without

- Messaggio: 1764 di 4589
- Iscritto il: 22/10/2016, 17:52
Re: Problema di combinatoria
ZfreS ha scritto:Non considero {1,2} e {2,1} come sottoinsiemi diversi.
Nemmeno io. Mancano tutti i sottoinsiemi di tre elementi, così come quelli di quattro elementi.
ZfreS ha scritto:L'algoritmo deve prestarsi bene anche per insiemi di 50 elementi. Quindi penso che l'approccio ricorsivo non sia la miglior soluzione.
Mmm, 50 sono tanti in effetti :S
Ho risolto l'esercizio al volo e lo sto eseguendo in Python. Non è una passeggiata con 50 elementi.
Se li vuoi conservare tutti in memoria avrai anche problemi di spazio. Qual è esattamente il tuo obiettivo?
Un matematico ha scritto:... come mia nonna che vuole da anni il sistema per vincere al lotto e crede che io, in quanto matematico, sia fallito perché non glielo trovo

-

Raptorista - Moderatore

- Messaggio: 5281 di 9616
- Iscritto il: 28/09/2008, 19:58
Re: Problema di combinatoria
Hai ragione, mancano tutti gli altri, quindi deve essere semplice. Tu hai già implementato? Beh, non li devo conservare in memoria, dato che il fine dell'esercizio non è tanto la gestione delle risorse quanto l'algoritmo che crea e ordina i sottoinsiemi.
- ZfreS
- Cannot live without

- Messaggio: 1765 di 4589
- Iscritto il: 22/10/2016, 17:52
Re: Problema di combinatoria
Ok, ma generarli in ordine qualsiasi e poi ordinarli è più semplice che generarli direttamente in ordine. Se non li puoi memorizzare tutti insieme significa che li devi generare già nell'ordine giusto.
Un matematico ha scritto:... come mia nonna che vuole da anni il sistema per vincere al lotto e crede che io, in quanto matematico, sia fallito perché non glielo trovo

-

Raptorista - Moderatore

- Messaggio: 5282 di 9616
- Iscritto il: 28/09/2008, 19:58
Re: Problema di combinatoria
Ok, mettiamola in questo modo: i numeri disordinati verranno memorizzati in un array nel main, non a runtime; poi man mano che vengono ordinati vengono anche memorizzati (non se ne può fare a meno). L'importante ora è capire come funziona l'algoritmo.
- ZfreS
- Cannot live without

- Messaggio: 1766 di 4589
- Iscritto il: 22/10/2016, 17:52
Re: Problema di combinatoria
Se ho ben capito, nel caso in cui gli elementi fossero $n=5$, il risultato dovrebbe essere il seguente?
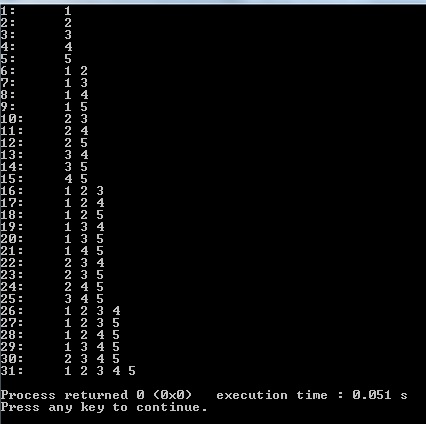
Secondo me la cosa più semplice è implementare una funzione in grado di generare tutte le combinazioni semplici di $n$ elementi presi $k$ alla volta e poi mettere tale funzione all'interno di un ciclo che fa variare $k$ da 1 a $n$.

Secondo me la cosa più semplice è implementare una funzione in grado di generare tutte le combinazioni semplici di $n$ elementi presi $k$ alla volta e poi mettere tale funzione all'interno di un ciclo che fa variare $k$ da 1 a $n$.
Chi dorme in democrazia, si sveglia in dittatura.
- Super Squirrel
- Senior Member

- Messaggio: 355 di 1486
- Iscritto il: 16/05/2013, 22:05
44 messaggi
• Vai alla pagina... • 1, 2, 3, 4, 5
Chi c’è in linea
Visitano il forum: Nessuno e 1 ospite