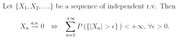6 messaggi
• Pagina 1 di 1
Legge dei grandi numeri - Ipotesi forte e debole
Scusate visto la sconfinata mole di teoremi che portano tutti il nome di Legge dei grandi Numeri, mi sta venendo un dubbio sulle ipotesi, in entrambi i casi tutti i termini $X_i$ della successione di variabili casuali $X_n$ devono essere i.i.d. e avere STESSA MEDIA E STESSA VARIANZA (FINITA)?
Una stanza senza un libro è come un corpo senz'anima.
Cicerone
Cicerone
-

squalllionheart - Senior Member

- Messaggio: 1211 di 1625
- Iscritto il: 18/07/2007, 16:26
- Località: Roma
Re: Legge dei grandi numeri - Ipotesi forte e debole
In realtà l'ipotesi che le variabili siano identicamente distribuite non è strettamente necessaria. E' sufficiente che siano indipendenti e che valga il Criterio di Kolmogorov, ovvero che la serie $Sigma_n (V(X_n))/n^2<oo$
Comunque sì, i teoremi sono parecchi....però gli esercizi sono interessanti; posta qualche esempio che ne discutiamo sicuramente insieme con mutua soddisfazione.
Esempio:
prendiamo la successione di variabili ${X_n}$ indipendenti$X_n={{: ( 0 , sqrt(n) ),( 1-1/sqrt(n) , 1/sqrt(n) ) :}$
(che evidentemente non sono identicamente distribuite)
Si può usare la SLLN per provare che $bar(X)_n\stackrel(" q.c. ")rarr 1$
Comunque sì, i teoremi sono parecchi....però gli esercizi sono interessanti; posta qualche esempio che ne discutiamo sicuramente insieme con mutua soddisfazione.
- tommik
- Moderatore

- Messaggio: 5008 di 11278
- Iscritto il: 23/04/2015, 13:13
- Località: Cassano Magnago
Re: Legge dei grandi numeri - Ipotesi forte e debole
Grazie, mi servirebbe qualche esempio sulla convergenza, per capire bene la definizione tra convervengenza in probabilità e quasi certa.
Una stanza senza un libro è come un corpo senz'anima.
Cicerone
Cicerone
-

squalllionheart - Senior Member

- Messaggio: 1212 di 1625
- Iscritto il: 18/07/2007, 16:26
- Località: Roma
Re: Legge dei grandi numeri - Ipotesi forte e debole
domani metto giù qualche esempio e controesempio
- tommik
- Moderatore

- Messaggio: 5011 di 11278
- Iscritto il: 23/04/2015, 13:13
- Località: Cassano Magnago
Re: Legge dei grandi numeri - Ipotesi forte e debole
Perfetto, che questi mesi ci divertiamo 
Una stanza senza un libro è come un corpo senz'anima.
Cicerone
Cicerone
-

squalllionheart - Senior Member

- Messaggio: 1213 di 1625
- Iscritto il: 18/07/2007, 16:26
- Località: Roma
Re: Legge dei grandi numeri - Ipotesi forte e debole
Vediamo un esempio semplice semplice ma che si presta a diverse interpretazioni
Consideriamo una successione di variabili aleatorie ${X_n}_(n in NN)$ con la seguente distribuzione
$X_n={{: ( 0 , 1),( 1-1/n , 1/n):}$
E' evidente che, se la successione converge in qualche senso, converge a zero, dato che la probabilità che le variabili valgano 1 è sempre più bassa al crescere di $n$
Le variabili non sono identicamente distribuite, dato che sono bernulliane di parametro variabile $1/n$ e, per il momento, non facciamo nemmeno ipotesi di indipendenza...
Per vedere l'ovvia consistenza ovvero la convergenza in probabilità, basta usare la definizione
$lim_(n rarr +oo)mathbb{P}[X_n>epsilon]=1/n rarr 0$
e quindi scriviamo $X_n\stackrel(" "mathcal(P)" ")rarr0$ ovvero la successione converge in probabilità a zero senza fare alcuna ipotesi di indipendenza o identica distribuzione.
Ora supponiamo che le variabili siano indipendenti. Per provare o confutare la convergenza quasi certa utilizziamo il Lemma di Borel Cantelli (che, in caso di indipendenza1, è condizione necessaria e sufficiente per la convergenza q.c.)
$Sigma_n mathbb{P}[X_n>epsilon]=Sigma_n 1/n=oo$
La serie non converge, le variabili sono indipendenti, applico il secondo Lemma di BC e concludo che la successione, pur convergendo in probabilità, non converge q.c. a zero
Vediamo come cambiano le cose eliminando l'ipotesi di indipendenza delle variabili....
A questo punto la divergenza della serie non ci può dire più nulla perché il secondo lemma non è applicabile.
Però possiamo strutturare la successione in questo modo. Prendiamo una variabile $U$ uniforme in $[0;1]$ e riscriviamo la distribuzione delle variabili della nostra successione così:
$X_n={{: ( 0 , 1),( U>1/n , U<=1/n):}$
Così costruite, è evidente che
$mathbb{P}({u in U: lim_n X_n(u)=0})=1$
in quanto $X_n(u)=1$ soltanto quando $U=0$ ma $mathbb{P}[U=0]=0$
In sostanza, eliminando l'ipotesi di indipendenza abbiamo che $X_n\stackrel(" q.c. ")rarr0$
^^^^^^^^^^^^^^^^
Che con questa costruzione le variabili della successione non siano indipendenti si vede facilmente così:
Prendiamo due valori $m>n$ e calcoliamo la probabilità congiunta (basta fare un disegno per rendersene conto)
$mathbb{P}[X_n=1;X_m=1]=1/m !=1/mxx1/n$
Spero di averti chiarito un po' il problema... non è un argomento semplicissimo; cerca qualche esercizio, prova a risolverlo postando un topic per ogni esercizio e vedrai che qualcuno ti aiuterà sicuramente a chiarire meglio la questione. Per studiare la convergenza quasi certa ci sono diverse vie e, a seconda dell'esercizio, è opportuno scegliere la più comoda
1) Lemma di BC
2) caratteristiche della successione (monotonia e limitatezza)
3) Legge forte dei grandi numeri
4) Definizione
5) Conservazione della continuità (Continuous Mapping Theorems)
6) Altre proprietà
7) un mix delle precedenti
Saluti
Consideriamo una successione di variabili aleatorie ${X_n}_(n in NN)$ con la seguente distribuzione
$X_n={{: ( 0 , 1),( 1-1/n , 1/n):}$
E' evidente che, se la successione converge in qualche senso, converge a zero, dato che la probabilità che le variabili valgano 1 è sempre più bassa al crescere di $n$
Le variabili non sono identicamente distribuite, dato che sono bernulliane di parametro variabile $1/n$ e, per il momento, non facciamo nemmeno ipotesi di indipendenza...
Per vedere l'ovvia consistenza ovvero la convergenza in probabilità, basta usare la definizione
$lim_(n rarr +oo)mathbb{P}[X_n>epsilon]=1/n rarr 0$
e quindi scriviamo $X_n\stackrel(" "mathcal(P)" ")rarr0$ ovvero la successione converge in probabilità a zero senza fare alcuna ipotesi di indipendenza o identica distribuzione.
Ora supponiamo che le variabili siano indipendenti. Per provare o confutare la convergenza quasi certa utilizziamo il Lemma di Borel Cantelli (che, in caso di indipendenza1, è condizione necessaria e sufficiente per la convergenza q.c.)
$Sigma_n mathbb{P}[X_n>epsilon]=Sigma_n 1/n=oo$
La serie non converge, le variabili sono indipendenti, applico il secondo Lemma di BC e concludo che la successione, pur convergendo in probabilità, non converge q.c. a zero
Vediamo come cambiano le cose eliminando l'ipotesi di indipendenza delle variabili....
A questo punto la divergenza della serie non ci può dire più nulla perché il secondo lemma non è applicabile.
Però possiamo strutturare la successione in questo modo. Prendiamo una variabile $U$ uniforme in $[0;1]$ e riscriviamo la distribuzione delle variabili della nostra successione così:
$X_n={{: ( 0 , 1),( U>1/n , U<=1/n):}$
Così costruite, è evidente che
$mathbb{P}({u in U: lim_n X_n(u)=0})=1$
in quanto $X_n(u)=1$ soltanto quando $U=0$ ma $mathbb{P}[U=0]=0$
In sostanza, eliminando l'ipotesi di indipendenza abbiamo che $X_n\stackrel(" q.c. ")rarr0$
^^^^^^^^^^^^^^^^
Che con questa costruzione le variabili della successione non siano indipendenti si vede facilmente così:
Prendiamo due valori $m>n$ e calcoliamo la probabilità congiunta (basta fare un disegno per rendersene conto)
$mathbb{P}[X_n=1;X_m=1]=1/m !=1/mxx1/n$
Spero di averti chiarito un po' il problema... non è un argomento semplicissimo; cerca qualche esercizio, prova a risolverlo postando un topic per ogni esercizio e vedrai che qualcuno ti aiuterà sicuramente a chiarire meglio la questione. Per studiare la convergenza quasi certa ci sono diverse vie e, a seconda dell'esercizio, è opportuno scegliere la più comoda
1) Lemma di BC
2) caratteristiche della successione (monotonia e limitatezza)
3) Legge forte dei grandi numeri
4) Definizione
5) Conservazione della continuità (Continuous Mapping Theorems)
6) Altre proprietà
7) un mix delle precedenti
Saluti
- tommik
- Moderatore

- Messaggio: 5014 di 11278
- Iscritto il: 23/04/2015, 13:13
- Località: Cassano Magnago
6 messaggi
• Pagina 1 di 1
Torna a Statistica e probabilità
Chi c’è in linea
Visitano il forum: Nessuno e 1 ospite