Siano $ X $ e $ Y $ due variabili aleatorie caratterizzate dalla seguente pdf congiunta:
$ f_(XY)(x,y)={ ( alpha, AA(x,y)inD ),( 0,ALTRIMENTI ):} $
dove $ alpha $ è una costante reale e $ D={-1<=x<=1; max(-x,0)-1<=y<=min(-x,0)+1 }$
1) Dopo aver disegnato D, determinare il valore di $ alpha $ in modo che $ f_(XY)(x,y) $ sia una valida pdf;
2)Calcolare le pdf $ X $ e $ Y $, rappresentare graficamente e verificare che siano valide;
3)Calcolare il valore di $ P(X+Y>=0) $;
4) Stabilire se $ X $ e $ Y $ sono indipendenti e/o correlate.
Il punto 1) dovrebbe essere questo:
Il dominio dovrebbe essere questo qui salvo errori:

Per calcolarmi la mia PDF ho diviso il mio dominio in domini più semplici e poi ho calcolato l'integrale definito in quelle regioni dello spazio e poi li ho sommati così:

$ D_(1)={0<=x<=1; -1<=y<=0 }$ Quadrato IV quadrante
$ D_(2)={-1<=x<=0; 0<=y<=-x-1 }$ Triangolo III quadrante
$ D_(3)={-1<=x<=0; 0<=y<=1 }$ Quadrato II quadrante
$ D_(4)={0<=x<=1; 0<=y<=-x+1 }$ Triangolo I quadrante
$ PDF(D_1)=int_(0)^(1) int_(-1)^(0)alpha dxdy=alpha int_(0)^(1)[y]_(-1)^(0)dx=alpha int_(0)^(1) dx=alpha $
$ PDF(D_3)=int_(-1)^(0) int_(0)^(1)alpha dxdy=alpha int_(-1)^(0)[y]_(0)^(1)dx=alpha int_(-1)^(0) dx=alpha $
$ PDF(D_2)=int_(-1)^(0) int_(0)^(-x-1)alpha dxdy=alpha int_(-1)^(0)[y]_(0)^(-x-1)dx=alpha int_(-1)^(0) -x-1 dx= -alpha/2[x^2]_(-1)^(0)-alpha[x]_(-1)^(0)=3/2alpha$
$ PDF(D_4)=int_(0)^(1) int_(0)^(-x+1)alpha dxdy=alpha int_(0)^(1)[y]_(0)^(-x+1)dx=alpha int_(0)^(1) x+1 dx= -alpha/2[x^2]_(0)^(1)+alpha[x]_(0)^(1)=1/2alpha$
$ alpha+alpha+3/2alpha+1/2alpha=4alpharArr alpha=1/4 $
Detto ciò veniamo al problema di prima il punto 2):
Per fare le marginali devo determinare credo il dominio di $X$ e $Y$ e poi calcolarmi gli integrali:
$ D_(X)={-1<=x<=1 }$ quindi è una fascia che va da $-1$ a $1$ e questo dovrebbe essere la pdf marginale:
$f_(X)(x)=int_(-1)^(1) 1/4 dx=1/4 [x]_(-1)^(1)=2 1/4=1/2 $
Salvo imprevisti credo di aver fatto bene ma non mi meraviglio mai della mia ciucciagine ora tocca a $ Y $:
Questo abbiamo era il dominio di $ D={-1<=x<=1; max(-x,0)-1<=y<=min(-x,0)+1 }$
Quindi questo :
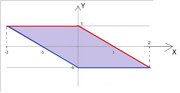
Il punto era che estremi di integrazione metto per la mia marginale di $f_(Y)(y)$?
Posso mai considerare questi due domini e intersecarli? Se la somma degli integrali è pari all'unione dei domini di dove è definita la funzione la differenza tra integrali è l'intersezione? O sto dicendo una fesseria ENORME?

Quindi considerare prima il dominio $ A={1<=y<=-1;}$
$f_(YA)(y)=int_(1)^(-1) 1/4 dy=1/4 [y]_(1)^(-1)=2 1/4=1/2 $
Quindi considerare prima il dominio $ B={-x+1<=y<=-x-1;}$
$f_(YB)(y)=int_(-x+1)^(-x-1) 1/4 dx=1/4 [y]_(-x+1)^(-x-1)=2 1/4=1/2 $
quindi chi sottraggo a chi è indifferente in questo caso?
$f_(Y)(y)=f_(YA)(y)-f_(YB)(y)=1/2 -1/2 =0$
Scusatemi per l'ignoranza, spero di non aver detto troppe fesserie