Esercizio 1
Su un campione casuale di 20 negozi di musica di una regione italiana la media settimanale di dischi di musica Jazz venduti e' risultata pari a 160 con deviazione standard 46. In una diversa regione italiana su un campione casuale di 15 negozi la corrispondente media e' risultata pari a 90 con deviazione standard 35. Sotto l’ipotesi di normalita' del numero di dischi Jazz venduti settimanalmente da ciascun negozio,
1. si costruisca un intervallo di confidenza di livello 90% per la vera media
settimanale di dischi Jazz venduti da un negozio nella prima regione.
2. si verifichi al livello 5% l’ipotesi che non vi sia differenza significativa
nelle vendite medie settimanali di musica Jazz di un negozio tra le due
regioni, contro l’ipotesi che il Jazz sia pi`u popolare nella prima regione.
Banalmente la prima si costruisce con
$I=[\bar{X} +- t_{\alpha/2, 19} s/sqrt{n} ]$
Primo problema nella soluzione parla non di $t_{\alpha/2, n-1} $ ma di t_{0,95, 19}
Dove lo prendo il valore di una t student con 19 gradi di libertà???
Aiutatemi perchè sto in fase di delirio.
Visto che
$\alpha=90%$
$I=[\bar{X} +- t_{0.45, 19} 46/sqrt{20} ]$
3 messaggi
• Pagina 1 di 1
Intervallo di confidenza media con varianza ignota
Una stanza senza un libro è come un corpo senz'anima.
Cicerone
Cicerone
-

squalllionheart - Senior Member

- Messaggio: 1222 di 1625
- Iscritto il: 18/07/2007, 16:26
- Località: Roma
Re: Intervallo di confidenza media con varianza ignota
squalllionheart ha scritto:Primo problema nella soluzione parla non di $t_{\alpha/2, n-1} $ ma di t_{0,95, 19}
e dove sta la differenza? alcuni indicano $alpha/2$ altri $1-alpha/2$ perché alcuni si riferiscono a $P(T<t)$ altri $P(T>t)$ ma il valore sempre quello è.....lo prendi dalle tavole: $t=1.729$
Oppure usi un calcolatore, va bene anche Excel; con Excel lui ti dà già il quantile di destra ma riferito all'intervallo bilaterale, quindi basta digitare $+"INV.T"(alpha;"gl")$ ovvero nel tuo caso$+"INV.T"(0.1;19)$ per ottenere il risultato corretto: $1.729$
Ecco entrambi gli esempi con due tavole differenti dove però è sempre chiaramente specificato a cosa ci si riferisce e dunque non c'è modo di sbagliarsi....(conoscendo la teoria, ovviamente)
(click per ingrandire)
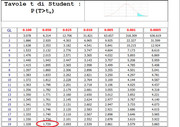
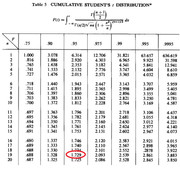
Se viene detto " intervallo di confidenza al 90%" è ovvio che $alpha=10%$...se l'intervallo è bilaterale toglierai il 5% a sinistra ed il 5% a destra....
Se ti dicono "test a livello 5%" significa "ampiezza del test", ovvero "livello di significatività del test", ovvero $alpha=5%$
Ad ogni modo devi escludere sempre le code della distribuzione che saranno l'1%, il 2.5%, il 5% ecc ecc....o no?
squalllionheart ha scritto:Visto che
$\alpha=90%$
$I=[\bar{X} +- t_{0.45, 19} 46/sqrt{20} ]$
$alpha=90%$
](./images/smilies/eusa_wall.gif)
](./images/smilies/eusa_wall.gif)
](./images/smilies/eusa_wall.gif)
...ma hai idea di cosa significhi nella realtà fare una cosa del genere??? (domanda retorica)
Per risolvere entrambi i punti basta ricopiare le formule dal libro e sostituire i valori della traccia....
- tommik
- Moderatore

- Messaggio: 5092 di 11278
- Iscritto il: 23/04/2015, 13:13
- Località: Cassano Magnago
Re: Intervallo di confidenza media con varianza ignota
Grazie!!!!!!
Una stanza senza un libro è come un corpo senz'anima.
Cicerone
Cicerone
-

squalllionheart - Senior Member

- Messaggio: 1223 di 1625
- Iscritto il: 18/07/2007, 16:26
- Località: Roma
3 messaggi
• Pagina 1 di 1
Torna a Statistica e probabilità
Chi c’è in linea
Visitano il forum: Nessuno e 1 ospite